第1.3章：线性回归（Linear Regression）_模型评估

来源：大话线性回归（二）、大话线性回归（三）

本文为待加深学习内容，在此仅列举了框架，详细技术参考上面两篇来源

简述一下线性回归流程：首先可以进行数据的预处理，包括但不限于：缺失值处理、线性相关的特征值处理、误差较大的脏数据处理。然后搭建一个线性回归模型，运用梯度下降或者正规方程法可以求出参数，这样模型就确定了。之后再用一些检测方法，评估模型是否合理并进行针对性的优化。

文中$\hat{y}$为预测值，$y^{(i)}$为实际值，$x_i$表示第$i$个变量（特征），$x^{(i)}$表示第$i$组数据（样本），同理$x_n^{(m)}$表示第m个样本的第n个特征

一、线性回归算法原理推导

二、线性回归参数的求解（求函数最小值）

三、线性回归的模型评估

• 通过一、二的介绍，一个初步的预测模型搭建起来了。
• 这个模型的效果如何？如何评判这个效果？最初关于线性模型的假设成立吗？如何验证这些假设？还会有其它问题会影响模型效果吗？带着这些问题，将展开以下内容。

1.线性回归拟合优度

回归直线与各观测点的接近程度称为回归直线对数据的拟合优度。
拟合优度的百度百科

判断系数（较常用）

• 评判直线拟合优度需要一些指标，其中一个就是判定系数，也叫$R^2$检验，他的意义是由$x$引起的影响占总影响的比例来判断拟合程度的。
• $SST=\sum {\left(y_i-\overline{y}\right)}^2$　　　总平方和：真实值与均值的差值平方和。　　$SST=SSR+SSE$
  $SSR=\sum {\left({\hat{y}}_i-\overline{y}\right)}^2$　　回归平方和：预测值与均值的差值平方和。　　来自于特征值$x$的影响
  $SSE=\sum {\left(y_i-{\hat{y}}_i\right)}^2$　　残差平方和：真实值与预测值的差值平方和。　来自于误差$\mathbf{\epsilon }$的影响
• 我们希望来自无法预测的干扰项的影响尽可能的小，也就是说$x$影响占比越高，预测效果就越好，也即$SSR/SST$越大，直线拟合越好。由此引出判定系数的定义，我们一般称为$R^2$
  $$R^2=\frac{SSR}{SST}=\frac{\sum {\left({\hat{y}}_i-\overline{y}\right)}^2}{\sum {\left(y_i-\overline{y}\right)}^2}=1-\frac{\sum {\left(y_i-{\hat{y}}_i\right)}^2}{\sum {\left(y_i-\overline{y}\right)}^2}$$

估计标准误差

• 估计标准误差$s_e$是均方残差的平方根，可以度量各实际观测点在直线周围散布的情况。$s_e$反映了预测值与真实值之间误差的大小，$s_e$越小说明拟合度越高，反之$s_e$越大说明拟合度越低。
• $$s_e=\sqrt{\frac{\sum {\left(y_i-{\hat{y}}_i\right)}^2}{n-2}}=\sqrt{\frac{SSE}{n-2}}=\sqrt{MSE}$$

2.线性回归的显著性检验（不是很懂）

• 要想知道我们根据样本拟合的模型是否可以有效地预测或估计，我们需要对拟合的模型进行显著性检验，主要包括线性关系检验、回归系数检验。
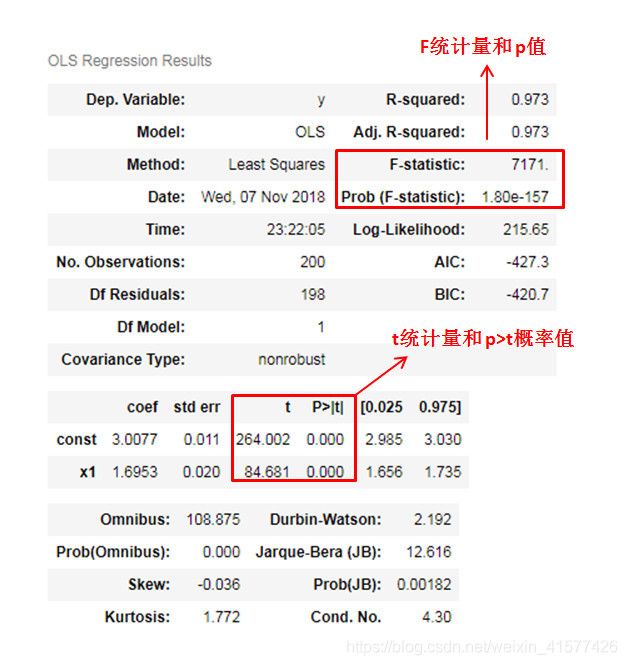
• 为了方便可以直接通过statsmodels模型引入ols模型进行回归拟合，然后查看总结表，其中包括F和t统计量结果。类似于下图
  　　　　　　

线性关系检验（emm…）

• 写在前面：F分布咋用啊？？。。。。还有就是好像没啥用啊，直接看求出的参数$\theta$是否全为0不就好了？？
• 线性关系检验是指多个自变量x和因变量y之间的线性关系是否显著，它们之间是否可以用一个线性模型表示。
• 检验统计量使用F分布，其定义如下：$$F=\frac{SSR/k}{SSE/(n-k-1)}=\frac{MSR}{MSE}\sim F(k,n-k-1)$$ SSR的自由度为：自变量的个数k，SSE的自由度为：n-k-1
  如果给定显著性水平$\alpha$，则根据两个自由度k和n-k-1进行F分布的查表。若$F>F_{\alpha }$，则拒绝原假设，说明发生了小概率事件，若$F<F_{\alpha }$，则不拒绝原假设。我们也可以直接通过观察$P$值来决定是否拒绝原假设，$P$值非常小，拒绝原假设，说明线性关系显著。
• 在多元线性回归中，只要有一个自变量系数不为零（即至少一个自变量系数与因变量有线性关系），我们就说这个线性关系是显著的。如果不显著，说明所有自变量系数均为零。

回归系数检验(emm…)

• 写在前面：t分布咋用啊？？。。。。还有就是好像依然没啥用啊，特征$x_i$对应的参数${\theta }_i$越大不就越重要吗？？
• 回归系数检验要求对每一个自变量系数进行检验，然后通过检验结果可判断一个特征（自变量）的重要性，并对特征进行筛选。
• 检验统计量使用t分布，其定义如下：$$\begin{array}{rl}{t}_i& =\frac{{\hat{\beta }}_i}{s_{{\hat{\beta }}_i}}\sim t(n-k-1)\\ s_{{\beta }_i}& =\frac{s_e}{\sqrt{\sum x_i^2-\frac{1}{n}{\left(\sum x_i\right)}^2}}\end{array}$$如前面一样，我们需要根据自由度n-k-1查t分布表，并通过$\alpha$或者$P$值判断显著性。$P>|t|的概率值$均为0，拒绝原假设，说明回归系数也都显著

3.线性回归的诊断

比较重要的几个有：（1）残差分析、（2）线性相关性检验、（3）多重共线性分析、（4）强影响点分析

残差分析（验证关于误差的假设）

• 线性回归模型一开始是基于一个假设：误差${\mathbf{\epsilon }}^{(i)}$是独立的并且具有相同的分布，并且服从均值为0，方差为${\sigma }^2$的高斯分布。
• 总结一下关于残差有三点假设：（1）正态性检验；（2）独立性检验；（3）方差齐性检验。下面我们将对这些假设逐一诊断，只有假设被验证，模型才是成立的。

正态性检验

1. 直方图法（应该比较靠谱）
   在一张图中画出误差分布的直方图以及标准正态分布，主要是通过目测对比进行检验。下图就属于一个拟合不好的例子。
   　　　　　　　　　　　　　　　　　　
2. PP图和QQ图

• PP图是对比正态分布的累积概率值和实际分布的累积概率值。QQ图是通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况。对应于正态分布的QQ图，就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图。图形类似下图：
  　　
  pp图和QQ图判断标准是：如果观察点都比较均匀的分布在直线附近，就可以说明变量近似的服从正态分布，否则不服从正态分布。上图的例子有的地方有一些较大的偏差，因此判断不是正态分布。
• statsmodels中直接提供了该检测方法。

3. Shapiro检验
   这种检验方法均属于非参数方法，先假设变量是服从正态分布的，然后对假设进行检验。一般地数据量低于5000则可以使用Shapiro检验，大于5000的数据量可以使用K-S检验，这种方法在scipy库中可以直接调用

独立性检验

• 残差的独立性可以通过Durbin-Watson统计量（DW）来检验。DW统计量公式如下：$$DW=\frac{{\sum }_{t=2}^T{\left({\hat{u}}_t-{\hat{u}}_{t-1}\right)}^2}{{\sum }_{t=1}^T{\hat{u}}_t^2}=2(1-\hat{p})$$ 判断标准是：
  p=0，DW=2：扰动项完全不相关
  p=1，DW=0：扰动项完全正相关
  p=-1，DW=4：扰动项完全负相关
• 上图中的statsmodels结果表中就包含了DW统计量，DW值为2.192，说明残差之间是不相关的，也即满足独立性假设。
  　　　　　　　　　　　

方差齐性检验

如果残差随着自变量增长发生随机变化，上下界基本对称，无明显自相关，方差为齐性，我们就说这是正常的残差。

1. 画图法
   图形法就是画出自变量与残差的散点图，自变量为横坐标，残差为纵坐标。下图就是一个例子，可以看出：残差的方差（即观察点相对红色虚线的上下浮动大小）不随着自变量变化有很大的浮动，说明了残差的方差是齐性的。
   　　　　　　　　　　　
2. BP检验法
   这种方法也是一种假设检验的方法，其原假设为：残差的方差为一个常数，然后通过计算LM统计量，判断假设是否成立。在statsmodels中也同样有相应的方法可以实现BP检查方法。

多重共线性检验

多重共线性的影响

• 多重共线性：如果存在一组不全为零的数${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r$，使得${\alpha }_1{X}_{i_1}+{\alpha }_2{X}_{i_2}+\dots +{\alpha }_r{X}_{i_r}=0$，则称线性回归模型存在完全共线性；如果存在随机误差$v$，满足$Ev=0,E{v}^2<\infty$，使得${\alpha }_1{X}_{i_1}+{\alpha }_2{X}_{i_2}+\dots +{\alpha }_r{X}_{i_{\mathrm{r}}}+v=0$，则称线性回归模型存在非完全共线性。
• 当回归模型中两个或两个以上的自变量彼此线性相关时，则称回归模型中存在多重共线性，也就是说共线性的自变量提供了重复的信息。后果就是会造成回归系数，截距系数的估计非常不稳定，即整个模型是不稳定。很可能回归系数原来正，但因为共线性而变为负。
• 举个例子：一个二元线性回归模型，自变量是x1和x2，因变量y，是一个三维的坐标系。假如x1和x2之间没有多重共线性，那么这个模型就是一个确定了的超平面。但假如x1和x2有很强的多重共线性，那么这个模型就近似是一个直线向量，而以这个直线所拟合出来的平面是无数个的（穿过一条直线的平面是不固定的）。这也就造成了回归系数的不确定性，以及模型无法稳定。

多重共线性的检测

多重共线性有很多检测方法，最简单直接的就是计算各自变量之间的相关系数，并进行显著性检验。具体的，如果出现以下情况，可能存在多重共线性：
（1）模型中各对自变量之间显著性相关。
（2）当模型线性关系（F检验）显著时，几乎所有回归系数的t检验不显著。
（3）回归系数的正负号与预期的相反。
（4）方差膨胀因子（VIF）检测，一般认为VIF大于10，则存在严重的多重共线性。

多重共线性的应对

多重共线性对于线性回归是种灾难，并且我们不可能完全消除，而只能利用一些方法来减轻它的影响。对于多重共线性的处理方式，有以下几种思路：
（1）提前筛选变量：可以利用相关检验来或变量聚类的方法。注意：决策树和随机森林也可以作为提前筛选变量的方法，但是它们对于多重共线性帮助不大，因为如果按照特征重要性排序，共线性的变量很可能都排在前面。
（2）子集选择：包括逐步回归和最优子集法。因为该方法是贪婪算法，理论上大部分情况有效，实际中需要结合第一种方法。
（3）收缩方法：正则化方法，包括岭回归和LASSO回归。LASSO回归可以实现筛选变量的功能。
（4）维数缩减：包括主成分回归（PCR）和偏最小二乘回归（PLS）方法。

强影响点分析

• 强影响点指的就是离散点，如果有一些离散点远离大部分数据，那么拟合出来的模型可能就会偏离正常轨迹。因此，在做线性回归诊断分析的时候也必须把这些强影响点考虑进去，进行分析。
• 我自己琢磨的话，用matplotlib画出箱型图来，也能去除掉一部分偏离程度较大的值。关于箱型图
• 针对于强影响点分析，一般的有以下几种方法：
  以下四个指标可以通过statsmodels直接查找到，对于我们建立的模型model自动检测每个样本的指标值是多少，只需要设置相应的临界点来判断就可以完成检测了。
  （1）学生化残差（SR）
  指的是残差标准化后的数值。一般的当样本量为几百时，学生化残差大于2的点被视为强影响点，而当样本量为上千时，学生化残差中大于3的点为相对大的影响点。
  （2）Cook’s D统计量
  测量当第$i$个观测值从分析中去除时，参数估计的改变程度。一般的Cook’s D值越大说明越可能是离散点，没有很明确的临界值。建议的影响临界点是：Cook’s D > 4/n，即高于此值可被视为强影响点。$${\text{Distance}}_i=\frac{1}{p+1}\frac{h_{ii}}{1-h_{ii}}{r}_i^2$$
  （3）DFFITS统计量
  用于测量第i个观测值对预测值的影响。建议的临界值为：$\left|DFFIT{S}_i\right|>2\sqrt{\frac{p}{n}}$
  （4）DFBETAS统计量
  用于测量当去除第i个观测量时，第j个参数估计的变化程度。建议的影响临界值为：$\left|DFBETA{S}_{ij}\right|>2\sqrt{\frac{1}{n}}$