【两次过】Lintcode 77. 最长公共子序列

给出两个字符串，找到最长公共子序列(LCS)，返回LCS的长度。

样例

样例 1:
	输入:  "ABCD" and "EDCA"
	输出:  1
	
	解释:
	LCS 是 'A' 或  'D' 或 'C'


样例 2:
	输入: "ABCD" and "EACB"
	输出:  2
	
	解释: 
	LCS 是 "AC"

---

解题思路：

动态规划。

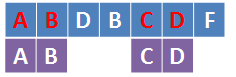
例子：ABCD 和ABDBCDF

它的最长公共子序列其实是ABCD，怎么回事呢？把它画出来就清楚了：

子序列并不要求这几个字符是连续出现的，只要相对顺序不变就可以了。也就是说，A必须在B前面，B在C前面，C在D前面就好了，并不要求B后面紧跟着就是C。

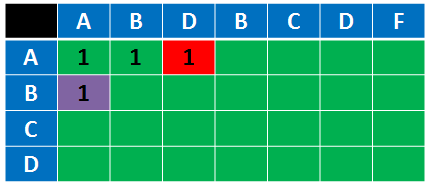
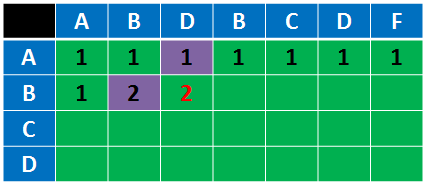
第i行第j列的格子里面的数字表示ABCD的前i个字符与ABDBCDF的前j个字符之间的最长公共子序列长度。

这里我们对比一下可以知道，红色框跟紫色框的数值都跟前面不一样了。

紫色框是第2行第1列，表示ABCD的前2个字符跟ABDBCDF的前1个字符之间的最长公共子序列长度，也就是AB与A之间的最长公共子序列长度，自然就是1了…

同理，红色框的1代表A与ABD之间的最长公共子序列长度。

接下来还是直接讲怎么求解这张表，边讲边解释，最后再做总结。

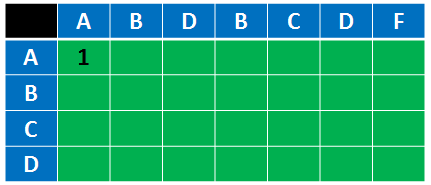
首先是最左上角这个元素的值，这是要初始化的，由于行列都是A，所以这个值是1：

然后接下来从左往右求第一行的所有值，这里我先直接把结果贴出来，先不要想怎么求，先看懂后面那几行怎么求就知道这个要怎么求了，当然第二行第一列的也先不管怎么求，后面会解释：

接下来就看红色格子要怎么求了：

这个格子表示的是AB与AB的最长公共子序列长度，那自然是2了，关键是，怎么来的？

我们先看看它左边、上边、左上那三个格子的意义：

1、 左边：AB与A的最长公共子序列长度

2、 上边：A与AB的最长公共子序列长度

3、 左上：A与A的最长公共子序列长度

 

而红色格子是AB与AB，是在它左上的基础上，两个字符串都增加一个字符，并且是相同的字符，所以它的最长公共子序列是不是就应该是它左上的格子数值加1？

给两个字符串都增加一个相同的字符，那么是不是它的最长公共子序列长度就是原来的加1？比如ABCD与ATC的最长公共子序列是AC，那我给它们两个后面都加个E，是不是它们（ABCDE与ATCE）的最长公共子序列就变成了ACE，长度就增加了1？

所以这一步求解的结果应该是这样的，我们把它左上的数字也标红了，表示它是有它左上的格子加1得到的：

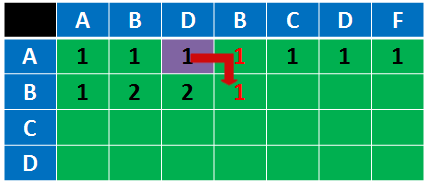
接下来继续求解下一个红色格子：

首先我们还是来看这个格子的意义：AB与ABD的最长公共子序列长度，所以结果依然是2，这个2应该怎么来？

依然是看它左边、上边、左上那三个格子的意义：

1、 左边：AB与AB的最长公共子序列长度

2、 上边：A与ABD的最长公共子序列长度

3、 左上：A与AB的最长公共子序列长度

 

我们先假设跟前面一样用左上这个格子，也就是说，从A与AB增加到AB与ABD，我只知道新增的两个字符不一样，哪里知道你会不会跟我原来前面的一样，所以这时候就不能用它来看了…

其实这是给两个字符串分别增加了一个不同的字符，拆开来看，其实就相当于先给其中一个增加一个字符，再给另一个增加一个字符，也就是有下面这两种情况：

1、 从A与AB，先给前面的A增加一个B，变成AB与AB（这时候最长公共子序列长度就变成2了），再给后面的AB增加一个D，变成AB与ABD

2、 从A与AB，先给后面的AB增加一个D，变成A与ABD（这时候最长公共子序列长度还是1），再给前面的A增加一个B，变成AB与ABD

 

因为我们知道新增的这两个字符是不一样的（如果是一样的，那么我们应该是按照上面描述的那种方式去计算，而不是这种方式），所以关键在于，新增的字符跟我原先的字符是否一样，就像这里，增加一个B和增加一个D，其实B是跟我前面一样的，所以最长公共子序列长度可以加1，这是在用第1种方式增加的时候就可以检测出来的，同理，有些时候你也可以从第二种方式检测出来，比如最简单的你把两个字符串调换过来就好了，从AB与A增加到ABD与AB，当然我们等下有个从AB与A增加到ABC与AB的例子…

既然两种方式都有可能检测出最长公共子序列长度加1，那么这里的最长公共子序列长度就应该是这两种方式里面较大的那个咯，所以就应该是它左边或者上边这两个格子之间较大的那个：

换句话讲，你可以有两种方式来获得这个值：

这种时候很明显就是应该取这个较大的了。

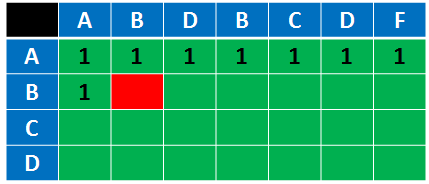
接下来继续往后求，中间就pass了，直接到刚刚说的ABC与AB的情况：

这时候，因为C != B，所以我们还是有两种方式，最终我们采取了上面的2：

所以除了第一行和第一列之外的所有格子，我们都会求解了，现在问题是，怎么求解第一行和第一列？

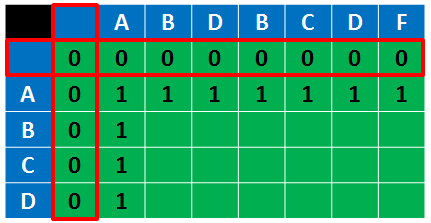
 做一步预处理，让第一行和第一列变成中间行中间列，无需特殊对待

我觉得你看看这个表格大概就能顿悟了：

在最上面跟最左边增加一行0和一列0就好了嘛，这些0的意义就是，字符串跟字符空串的最长公共子序列长度是0嘛

好的，接下来总结：

对于一个格子，如果行列字符相同，那么它的数值就是它左上格子的数值加1

如果行列字符不相同，那么它的数值就是它左边或者上边这两个格子的数值中较大的那个

---

设dp[i][j]为A[0...i]和B[0...j]的最长公共子序列的长度

当A[i] == B[j]时，说明这个字符可以作为最长公共子序列的一部分：dp[i][j] = 1 + dp[i-1][j-1]

当A[i] != B[j]时，说明这个字符不能作为公共子序列的一部分，所以考察i-1与j的情况和i与j-1的情况，取两者最大值：dp[i][j] = max(dp[i-1][j] , dp[i][j-1])

public class Solution {
    /**
     * @param A: A string
     * @param B: A string
     * @return: The length of longest common subsequence of A and B
     */
    public int longestCommonSubsequence(String A, String B) {
        // write your code here
        char[] a = A.toCharArray();
        char[] b = B.toCharArray();
        int res = 0;
        
        if(a.length == 0 || b.length == 0)
            return res;
        
        //dp[i][j]表示A序列前i个数，与B的前j个数的LCS长度
        int[][] dp = new int[a.length + 1][b.length + 1];
        
        for(int i=1; i<=a.length; i++){
            for(int j=1; j<=b.length; j++){
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                if(a[i-1] == b[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
            }
        }
        
        return dp[a.length][b.length];
    }
}

如果题目需要求出最长公共子序列是什么，就需要在dp时存储当前操作是由哪步过来的，利用temp数组存储，1代表从dp[i-1][j]过来，2代表从dp[i][j-1]过来，3代表从dp[i-1][j-1]过来。最后倒序依次整理出结果。因为算dp时就是倒序算的，由dp[i]倒推出用到了哪个dp[i-1]。

public class Solution {
    /**
     * @param A: A string
     * @param B: A string
     * @return: The length of longest common subsequence of A and B
     */
    public int longestCommonSubsequence(String A, String B) {
        // write your code here
        char[] a = A.toCharArray();
        char[] b = B.toCharArray();
        int res = 0;
        
        if(a.length == 0 || b.length == 0)
            return res;
        
        //dp[i][j]表示A序列前i个数，与B的前j个数的LCS长度
        int[][] dp = new int[a.length + 1][b.length + 1];
        //标记当前操作是从哪一步过来的
        int[][] temp = new int[a.length + 1][b.length + 1];
        
        for(int i=1; i<=a.length; i++){
            for(int j=1; j<=b.length; j++){
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                if(a[i-1] == b[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                
                //标记状态
                if(dp[i][j] == dp[i-1][j])
                    temp[i][j] = 1;
                else if(dp[i][j] == dp[i][j-1])
                    temp[i][j] = 2;
                else
                    temp[i][j] = 3;
            }
        }
        
        //从后向前倒序推出LCS
        int m = a.length;
        int n = b.length;
        
        char[] ans = new char[dp[m][n]];
        int cur = dp[m][n] - 1;
        
        while(m > 0 && n > 0){
            if(temp[m][n] == 1)//表示从dp[i-1][j]过来
                m--;
            else if(temp[m][n] == 2)//表示从dp[i][j-1]过来
                n--;
            else{                   //表示从dp[i-1][j-1]过来，并且此时的字符为结果之一
                ans[cur--] = a[m-1];
                m--;
                n--;
            }
        }
        
        //打印出LCS结果
        for(int i=0; i