【算法设计与分析】常用算法概述
一、【分治法】
分治法,字面上的解释是“分而治之”,就是把一个复杂的问题分成多个的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。
递归:直接或间接地调用自身的算法。(包括两个部分:递归的出口和递归函数的表达式)。
分治是一种思想,递归是实现这种思想的一种手段。
分治法所能解决的问题一般具有以下几个特征:
1) 该问题的规模缩小到一定的程度就可以容易地解决。
2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解。
4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
分治法的基本步骤:
分治法在每一层递归上都有三个步骤:
分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题;
合并:将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下:
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 将P分解为较小的子问题 P1 ,P2 ,...,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
6. T ← MERGE(y1,y2,...,yk) △ 合并子问题
7. return(T) 分治与减治的区别:
分治法主要是将问题分成若干个子问题,然后最后将问题合并起来,从而求得其解。
减治法是将问题分解,但是没有将解合并的过程,解就在子问题的解中。通常来说,减治法的效率较高。
举个例子:
求解a^n的结果
分治法:将a^n 问题分解为a^[n/2]*[n/2]问题,然后将最后的结果合并起来
减治法思路:将a分成奇数和偶数,然后把奇数偶数结果求出来,直接就可以得到结果了,所以原题目的结果就在子问题中,没有合并的过程。
二、【动态规划】
每次决策依赖于当前状态,又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
动态规划与分治法类似,也是将原问题分解为相对简单的子问题,然后从这些子问题中得到原问题的解。
动态规划常常适用于有重叠子问题和最优子结构性质的问题。
动态规划与分治法区别:
动态规划不是分治法,关键在于分解出来的各个子问题往往不是互相独立的。分治法要求各个子问题是独立的(即不包含公共的子问题),因此一旦递归地求出各个子问题的解后,便可自下而上地将子问题的解合并成原问题的解。如果各子问题是不独立的,那么分治法就要做许多不必要的工作,重复地解公共的子问题。
不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
问题特征:
(1)最优子结构:当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
(2)重叠子问题:在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,在以后尽可能多地利用这些子问题的解。
算法步骤:
(1)分析最优值的结构,刻画其结构特征;
(2)递归地定义最优值;
(3)以自底向上的方式计算最优值
(4)根据最优值得到的信息构造最优解
三、【贪心算法】
贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做的选择只是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
贪心算法通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
贪心算法与动态规划的区别:
共同点:两者都具有最优子结构性质
不同点:
1)动态规划算法中,每步所做的选择往往依赖于相关子问题的解,因而只有在解出相关子问题时才能做出选择。而贪心算法,仅在当前状态下做出最好选择,即局部最优选择,然后再去解做出这个选择后产生的相应的子问题。
2) 动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常自顶向下的方式进行。
四、【回溯算法】
回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含(剪枝过程),则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。这种方法适用于解一些组合数相当大的问题。
用回溯法解题的一般步骤:
(1)针对所给问题,定义问题的解空间;
(2)确定易于搜索的解空间结构;
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
回溯VS递归:
回溯是一种算法思想,递归是实现算法的一种手段。
回溯和递归唯一的联系就是,回溯法可以通过递归来实现。
五、【分支限界法】
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
常见的两种分支限界法:
(1)队列式(FIFO)分支限界法
按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。
(2)优先队列式分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
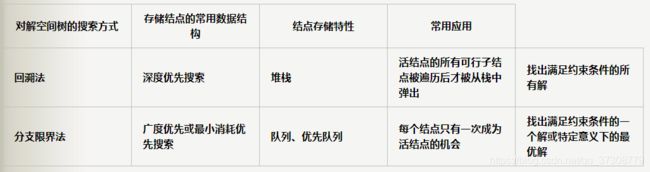
分支限界法与回溯法的不同:
(1)求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
(2)搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。