马踏棋盘(从低效到高效)
题目描述
将棋子“马”随机的放在国际象棋棋盘Board[8][8]的某个方格中,“马”按走棋规则进行移动,要求每个方格只进入一次,走遍棋盘上所有的64个方格。
题目要求
编写非递归程序,求出“马”的行走路线,并按求出的行走路线将数字1-64依次填入一个8x8的方阵并输出。
分析 x 1
一看题目说是8x8棋盘,要求走遍棋盘,首先想到的便是直接深搜即可,但是后面说到要求非递归程序,这也简单,自己把递归的那一部分
改为用栈来实现即可(马走棋盘肯定会遇到走不下去的情况,所以需要储存之前已经走过的点,而“悔棋”肯定是从当前这一步往之前返
回,所以是一个后进先出的结构——栈)。
定义
typedef struct _horse
{
int x; //横坐标
int y; //纵坐标
int s; //下一步的方向
}HORSE;
int chessboard[8][8]; //棋盘
int Next[8][2] = {
{
2,1}, {
1,2}, {
-1,2}, {
-2,1}, {
-2,-1}, {
-1,-2}, {
1,-2}, {
2,-1}}; //方向
int cnt = 1; //计数器
stack<HORSE> horse;
执行函数
bool judge(int a, int b)
{
if(a < 0 || a > 7 || b < 0 || b > 7) //边界
return false;
return true;
}
void Horse(int x, int y)
{
HORSE temp;
int a,b; //记录当前马位置附近的坐标
int i = 0;
chessboard[x][y] = cnt; //标记当前起始位置已被访问
temp.x = x; //记录当前马的位置
temp.y = y;
while(cnt < 64)
{
for(; i < 8; i++)
{
a = temp.x + Next[i][0];
b = temp.y + Next[i][1];
if(judge(a,b) && chessboard[a][b] == 0) //判断
{
break;
}
}
if(i < 8) //能够访问当前马位置附近的日点
{
chessboard[a][b] = ++cnt;
temp.s = i;
horse.push(temp);
memset(&temp, 0, sizeof(HORSE));
temp.x = a;
temp.y = b;
i = 0;
}
else //回溯
{
--cnt;
chessboard[temp.x][temp.y] = 0;
HORSE tt = horse.top();
horse.pop();
temp.x = tt.x;
temp.y = tt.y;
i = tt.s;
++i; //继续搜索从当前马位置访问的点的下一个点继续访问
}
}
}
完成后测试了一下,只有(0,0)可以跑出来,可见这种暴力的方式效率实在是太低…
分析 x 2
上面的暴力试探方式效率实在太低了,所以我们要优化一下代码。
把书继续往后翻,有提到将马的初始步入栈,计算其8个方向的权值,将其按升序排列,马从最小权值的点开始走,
无路可走时回溯(权值就是一个点下一步能走的点的总数)。
这是一种贪心的思想,那么既然是贪心,我们可不可以再贪心一些,每一步直接走权值最小的点,不再回溯,看能不能走完。
执行函数
void Horse(int x, int y)
{
HORSE temp;
int a,b; //记录当前马位置附近的坐标
chessboard[x][y] = cnt; //标记当前起始位置已被访问
temp.x = x; //记录当前马的位置
temp.y = y;
while(cnt < 64)
{
int h_min = 8; //权值最小的点
int tx,ty,ti; //记录权值最小的点的信息
for(int i = 0; i < 8; i++)
{
a = temp.x + Next[i][0];
b = temp.y + Next[i][1];
if(judge(a,b) && chessboard[a][b] == 0) //判断
{
int step = steps(a,b); //计算权值
if(step < h_min) //更新权值最小的点
{
h_min = step;
tx = a;
ty = b;
ti = i;
}
}
}
//直接走权值最小的点
chessboard[tx][ty] = ++cnt;
temp.s = ti;
//temp.step = h_min;
horse.push(temp);
memset(&temp, 0, sizeof(HORSE));
temp.x = tx;
temp.y = ty;
}
}
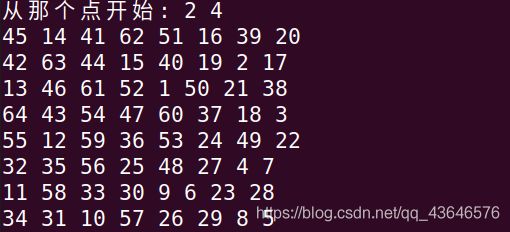
这次测试了一下,效率大大的提高了,但是我们是“最”贪心的方法,所以我们要测试一下,看能不能从任意点出发都能走完棋盘。
经过测试有一个点不能走完棋盘,就是(2,4),也就是三行五列的点。
分析 x 3
好吧,既然只有一个点不能按照我们最贪心的方式走完,那么我们就只对这一个点特殊处理一下。
处理方式即就是分析2时所说的按权值大小排序,从最小的开始走。
最终版本
#include