C语言-数据结构-骑士周游-马踏棋盘问题-源代码

1. 目标

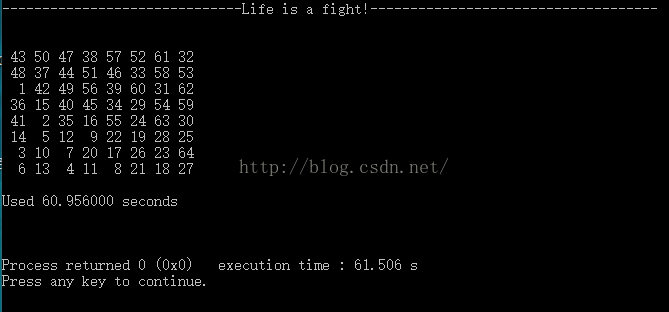
对于一个指定的起始坐标，按照‘马’的走棋规则，从该坐标开始搜索一条可以覆盖棋盘每个位置的走棋路径。例如下面是从（2，0）坐标开始搜索得到的一个解。

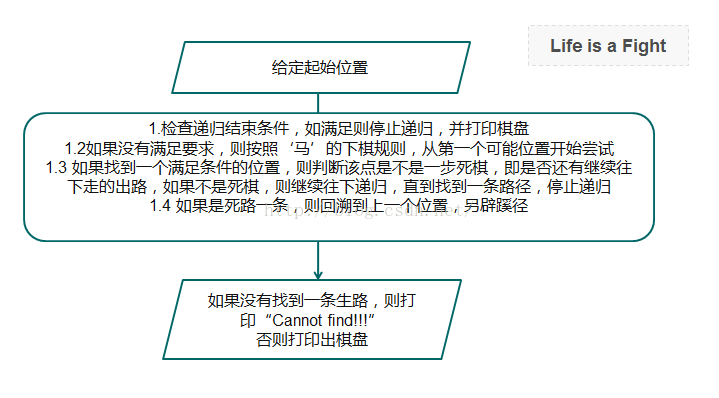
2. 代码结构

3. 源代码

该代码仅仅是寻找到一条生路，即停止。另外对选择的起始点，和寻找下一点的顺序不同（即sposition()中case的顺序不同，对于程序执行的时间影响会很大）。

另外程序中调用了time.h头文件中的clock相关函数，对代码的执行时间进行了统计，具体见代码。

#include
#include
#define title "------------------------------Life is a fight!------------------------------------"
#define X 8 //定义棋盘大小
#define Y 8

int chess[X][Y]= {
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0},
                {0,0,0,0,0,0,0,0}
              };

int sposition(int *x, int *y, int p)
{

    switch(p)//特别需要注意每个case 中的顺序，对程序执行的时间有很大影响
	{
		case 0:
			if( *x+2<=X-1 && *y-1>=0 && chess[*x+2][*y-1]==0 )
			{
				*x = *x + 2;
				*y = *y - 1;
				return 1;
			}
			else
                return 0;

		case 1:
			if( *x+2<=X-1 && *y+1<=Y-1 && chess[*x+2][*y+1]==0 )
			{
				*x = *x + 2;
				*y = *y + 1;
				return 1;
			}
			else
                return 0;

		case 2:
			if( *x+1<=X-1 && *y-2>=0 && chess[*x+1][*y-2]==0 )
			{
				*x = *x + 1;
				*y = *y - 2;
				return 1;
			}
			else
                return 0;

		case 3:
			if( *x+1<=X-1 && *y+2<=Y-1 && chess[*x+1][*y+2]==0 )
			{
				*x = *x + 1;
				*y = *y + 2;
				return 1;
			}
			else
                return 0;

		case 4:
			if( *x-2>=0 && *y-1>=0 && chess[*x-2][*y-1]==0 )
			{
				*x = *x - 2;
				*y = *y - 1;
				return 1;
			}
			else
                return 0;

		case 5:
			if( *x-2>=0 && *y+1<=Y-1 && chess[*x-2][*y+1]==0 )
			{
				*x = *x - 2;
				*y = *y + 1;
				return 1;
			}
			else
                return 0;

		case 6:
			if( *x-1>=0 && *y-2>=0 && chess[*x-1][*y-2]==0 )
			{
				*x = *x - 1;
				*y = *y - 2;
				return 1;
			}
			else
                return 0;

		case 7:
			if( *x-1>=0 && *y+2<=Y-1 && chess[*x-1][*y+2]==0 )
			{
				*x = *x - 1;
				*y = *y + 2;
				return 1;
			}
			else
                return 0;

		default:
			return 0;
	}
}

void prfChess(int t_chess[][Y])
{
    int i, j;
    for(i=0;i