论文阅读——椭圆检测算法 2018 使用梯度分析利用错误检测控制的精确椭圆检测

        本文是2018年《Pattern Recognition》期刊（2区SCI）上的一篇文章，是最新的椭圆检测，论文题目为《Accurate detection of ellipses with false detection control at video rates using a gradient analysis》，从标题来看，梯度分析是常用的，其中比较吸引我的地方是false detection control，在阅读的时候我会详细进行分析。Prasad文章对我在初期研究椭圆检测时提供了巨大的帮助。

〇 摘要部分

         视频序列下的椭圆检测是一个开放的挑战。作者提供的额方法采用弧段选择、智能组合、梯度信息的重复利用过来显著的在不影响检测性能的前提下减少计算复杂度。因此使用了较少计算量的几何性质，比如圆弧平滑度、曲线的相对位置和椭圆中心的置信区域。作者进行了参数敏感度分析，仿真数据集分析，实际数据集测试，效果良好1。

一 介绍部分

        椭圆检测应用：工业检验、医学诊断、交通标志识别、安全性、人脸识别、机器人平台的目标跟踪。

        椭圆检测有三种问题需要解决：遮挡椭圆、不完全椭圆、重叠椭圆。提高精度就会浪费大量时间，提高时间往往导致精度下降，本文在精度和时间上均有提升。

1.1 相关工作2

• 基于霍夫变换（HT） HT和其他几何方法组合的混合方法可以克服HT方法的缺点。例如，Cakir等人基于特征模型的HT变换提高了检测精度。Chen等人使得HT和边缘分割检测的优点结合在一起，使其可以在工业场景上得以实现。

• 基于边缘连接的（论文中说是边缘分割检测方法，方法上是一样的） Mei等人根据椭圆的曲率和凸性条件，采用直线段去逼近潜在的椭圆弧段。Bai等人使用椭圆的凸性去组合弧段来识别候选椭圆。Liu等人提出了一种分层的方法，基于一个事实：椭圆的任何部分都可以通过几何约束在椭圆重建中识别自身。作者认为，边缘分割的检测方法是检测图像中多个椭圆的最有效的方法，比HT的方法需要更少的计算成本，这种方法处理包含复杂背景，遮挡的图像时，检测精度下降。

        还有很多文章提出了代数函数和几何特征用于椭圆弧段的选择来提升椭圆检测精度。比如，弧段的对称性用于分解参数空间，减少聚类参数。距离度量用于实现一组弧段的配准。Mulleti等人依赖finite-rate-of-innovation signals的采样结构来从部分数据估计椭圆的参数。Chang Liu等人使用给定的相机内参矩阵拟合一个旋转曲面的横截面的椭圆投影。Jia等人使用一个投影不变算子来显著检出不希望候选并挑选椭圆。

1.2 提出的方法

• 弧段提取与分类。目的是提取出椭圆弧段，抛除无用信息。

• 椭圆检测。 每个像素的梯度信息用于将椭圆候选弧段分类到4个象限3。然后利用一个事实，同一个椭圆的弧段具有相同的椭圆中心。作者定义了两个几何约束，来识别可能属于同一个椭圆的弧段几何。我们使用mean-shift来找到这样一组弧段的中心，并在分解的参数空间中获得其他参数4。基于投票或者累计的方法会在噪声的情况下有损失，所以mean-shift方法可以缓解这个问题。

• 椭圆验证。椭圆验证的目的是为了剔除虚假椭圆。作者提出了一个几何的控制策略。

1.3 方法的创新性

        作者的算法在上述的几个步骤都有自己独特的创新点，对提升结果起到了良好的作用。而且提出算法的新颖特征是以最少的计算来实现当前任务，有效的提升了检测速度。关于作者给出的创新性，我将完全的翻译出来放在下面。

• 1 本文提出了一种结合弧段提取与弧段组合的椭圆检测方法。弧段检测设计重要的弧段分割步骤，我们在2，3中给出的创新点有助于在低的计算消耗上进行精确的弧段检测。使用几何约束进行弧段分组，在4，5点中有更多的讨论，保证椭圆检测的有效性并优化计算损耗。

• 2 在平滑弧段检测（smooth arc detection）的步骤中，作者提出了一种新的方法来识别精确的分裂点（突然变化的部分），来更好的从曲线中分割出平滑的可能属于椭圆的弧段。首先在大范围进行粗略的突变搜索，然后用更细的范围确定这些点。

• 3 作者仅仅使用一个不等式与角度向量来确认分裂点，相比于其他方法所使用的不等式。这提供了计算速度快的优点5。

• 4 包围盒包围一个弧所形成的向量方向用于精确的确定一个弧的凹凸性，在后面可以进行弧段分类。这加快的弧段组合的效率。

• 5 我们使用包围一个弧段的包围盒周长的一半和半轴长度的比率还衡量椭圆的完整性，来提高检测精度，这比其他更复杂的测量椭圆完整性的方法要快得多。

• 6 提出了一种基于由一个数学模型表达的椭圆的内在几何属性的错误检测控制的方法来决定检测结果，这种方法有效的避免了错误检测。

二 弧段的分割与分类

在这里我先列出文章出现的参数，免得后期阅读麻烦。

符号	描述
OBBmin O B B m i n	最小区域包围盒，是一个包围盒，数据类型是RotateRect(openCV)
threr t h r e r	包围盒 OBBmin O B B m i n 长边与短边的比值阈值
threa t h r e a	包围盒 OBBmin O B B m i n 的面积阈值
threθ t h r e θ	曲率阈值，用于识别turning corner
threp t h r e p	距离约束阈值
threcenter t h r e c e n t e r	椭圆几何中心确定阈值

2.1 预处理阶段

        使用自适应Canny边缘检测来得到边缘图。每个边缘点的表达形式为： pi=(xi,yi,ηi) p i = ( x i , y i , η i ) ，其中 xi,yi x i , y i 就是边缘点坐标， ηi η i 为每个边缘点对应的梯度方向。

        随后，为了获得没有分支的边缘线，曲线按照边缘方向被分为两类。由于图像的离散性，无法计算出像素处曲线的精确梯度方向。但是，作者感兴趣的是梯度的大致方向而非精确方向，因此使用一个正负性来表示方向。在论文中，如果方向落在1，3象限则认为是正方向，在2，4象限则为负方向。对于那些垂直或水平的方向的像素点，就直接抛弃。

        在同一方向上的两个连续边缘点的8连通性用于提取连通边缘曲线。对于那些短边缘线，直接剔除。然后计算出曲线的包围盒 OBBmin O B B m i n ，如果包围盒长边与短边的比值大于设定阈值 threr t h r e r ，则认为这个曲线近似为直线段或其直径非常大，表明这个椭圆的中心点不在图像中。如果这个包围盒的面积小于阈值 threa t h r e a ，说明这个直线段非常小，不足以提供有效的信息。这些情况的曲线会被抛弃。剩下的这些曲线会被认为是可能构成椭圆的曲线候选。

        这个小节的目的就是提取出候选曲线，这些曲线可能是椭圆的一部分。

2.2 弧段提取

        椭圆的边缘段是平滑且连续的，这是常识。在这个论文中，曲率的变化量和曲率的方向变化被称为转角和拐点。

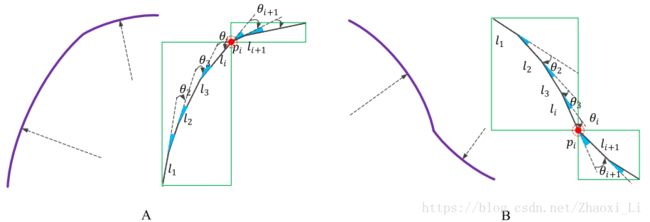
        首先使用一系列直线段对曲线进行逼近，目的就是方便估计曲线的曲率信息。作者提出了一种弧段分割算法。一个弧段用直线段逼近后，得到一组直线段 l1,l2,...,ln l 1 , l 2 , . . . , l n ， θi θ i 表示 li−1,li l i − 1 , l i 之间的夹角，也就是直线段方向的变化角度。如果 θi θ i 很小，表示这个点的曲率很小。如果 θi θ i 很大，则说明点 pi p i 附近曲率变化大，被认为是一个turning corner。如果 |θi|>threθ | θ i | > t h r e θ ，则 pi p i 是一个turning corner。

        椭圆的弧段变化方向应该具有相同的符号，如果符号不同，则这里存在拐点，作者使用 ||θi|−|θi−1||<|θi−θi−1| | | θ i | − | θ i − 1 | | < | θ i − θ i − 1 | 来识别拐点，其实这个公式就是三角不等式，如果这个式子两边相等，则说明是同一个方向，否则就说明方向不同，存在拐点。

        下图A表示的就是角度变化过大的点，图B表示是方向不同的拐点，在这两个点都将会将一个曲线分割为两个平滑曲线。

        在进行弧段分割时候，会有一些突变点导致弧段一分为二，并且产生小的弧段，论文的处理方式没看明白，给出的算法流程，个别符号有点混淆，我等源码下来之后更新这个突变点的处理问题。

2.3 基于凹凸性的弧段分类

        前面，作者根据梯度方向将弧段分为正负两个方向，在这里又根据弧段的凹凸性得到新的两个方向。然后将每个平滑弧段分类到4个象限中。分类方法很简单，这里不列公式说明。

        下图表示的是分类流程，原图检测到边缘之后，根据方向和弧段提取得到一组平滑曲线（图C），然后根据曲线的凹凸性，再次进行分类得到图（D）

三 椭圆检测

        我们从分布在4个象限的弧中选择两个弧段 τab=(aa,ab) τ a b = ( a a , a b ) 作为一个象限约束弧段集合，这个集合表示弧段有可能来自同一个椭圆。下标表示来自不同的象限，因此有六种不同的弧段组合， (aI,aII),(aI,aIII),(aI,aIV),(aII,aIII),(aII,aIV),(aIII,aIV) ( a I , a I I ) , ( a I , a I I I ) , ( a I , a I V ) , ( a I I , a I I I ) , ( a I I , a I V ) , ( a I I I , a I V ) 。进一步只保留满足相对位置约束的集合，并计算可能构成这些弧段的椭圆中心作为它们的边缘。然后我们基于弧段集合的中心的接近度创建这些弧段的超集。这是基于两个圆弧所估计的两个中心位于可接受范围的区域的情况下，这样的弧集极有可能属于同一椭圆。

3.1 构成一个椭圆的弧段选择

        作者提供了一个函数 Ω Ω 来表述两个弧段的相关距离约束来丢弃不满足同一个椭圆的弧段。

Ω(aa,ab)=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪alI(x)−arII(x)min(arI(y)−alIII(y),arI(x)−alIII(x))arI(y)−alIV(y)alII(y)−alIII(y)min(alII(y)−arIV(y),alIV(x)−arII(x))alIV(x)−arIII(x)if(aa,ab)∈(I,II)if(aa,ab)∈(I,III)if(aa,ab)∈(I,IV)if(aa,ab)∈(II,III)if(aa,ab)∈(II,IV)if(aa,ab)∈(III,IV) Ω ( a a , a b ) = { a I l ( x ) − a I I r ( x ) i f ( a a , a b ) ∈ ( I , I I ) m i n ( a I r ( y ) − a I I I l ( y ) , a I r ( x ) − a I I I l ( x ) ) i f ( a a , a b ) ∈ ( I , I I I ) a I r ( y ) − a I V l ( y ) i f ( a a , a b ) ∈ ( I , I V ) a I I l ( y ) − a I I I l ( y ) i f ( a a , a b ) ∈ ( I I , I I I ) m i n ( a I I l ( y ) − a I V r ( y ) , a I V l ( x ) − a I I r ( x ) ) i f ( a a , a b ) ∈ ( I I , I V ) a I V l ( x ) − a I I I r ( x ) i f ( a a , a b ) ∈ ( I I I , I V )

        其中， ali(x),ari(x),ali(y),ari(y) a i l ( x ) , a i r ( x ) , a i l ( y ) , a i r ( y ) 是沿着xy轴的最左端和最右端的坐标。对这个公式的解释可以参考上图， alI a I l 一定在 arII a I I r 的右边，即 alI(x)−arII(x) a I l ( x ) − a I I r ( x ) 一定大于0，其他同理。这个公式就是用来约束距离（这个公式原理上没有问题，但是似乎有的地方打错了，论文的解释是没有问题的。这个主要就是约束谁在左边，谁在上面的问题，等代码要到了我再细研究）。

        如果 Ω(aa,ab) Ω ( a a , a b ) 小于阈值 threp=1 t h r e p = 1 ，这个集合不可能构成一个椭圆，丢弃这个集合。参数 threp=1 t h r e p = 1 这个就是理论值，没有必要进行讨论，所以我觉得这个不算是参数。

3.2 椭圆中心的确认

        这个小节使用了大量的椭圆的几何性质。

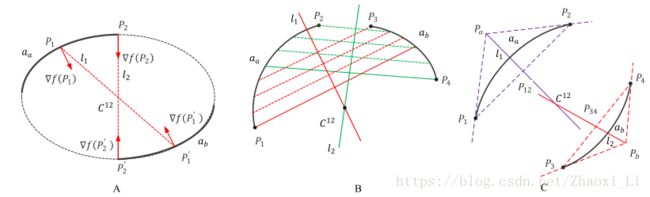
• 图A表示相对于椭圆中心对称的两个点的的梯度方向是共线或者反向共线的。

• 图B阐述了一个定理：在一对弧段上，通过两组不同的平行弦的中点的两条直线的交点是椭圆的中心点。但是这个方法对于小椭圆是无效的，因为小的椭圆对应的两组平行弦之间的距离较小，导致检测出的中心点误差较高。

• 图C是另一种利用几何性质得到椭圆中心点的方法。椭圆的中心点经过连接弦的中点和通过弧的末端由切线形成的交点的直线，那么两个弧段就会构成两个直线，其交点就是椭圆中心点。但是这个方法依赖于末端的梯度方向，梯度的误差直接影响检测的误差6。

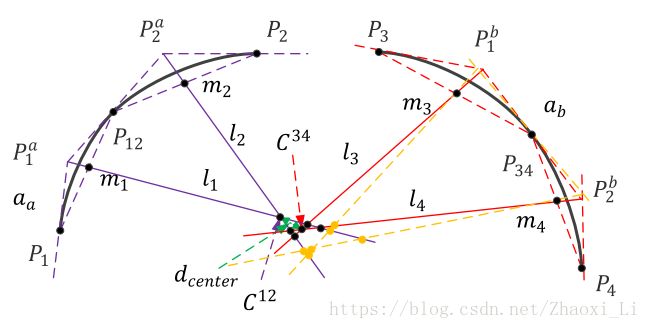
        作者提出了一个新的计算椭圆中心点的方法，这个方法不需要考虑椭圆的尺寸或精确的切线信息。不考虑椭圆尺寸是图C所示的优点，不需要精确的切线信息，不代表不适用，使用大量的直线就可以起到修正的作用，进而提高精度。

        下图就是作者使用的思想。以弧段 aa a a 为例，将一个弧段从中点分为两段得到三个点 P1,P12,P2 P 1 , P 12 , P 2 ，然后应用上述的思想得到直线 l1,l2 l 1 , l 2 ，进而得到一个中心点 C12 C 12 。同理得到 C34 C 34 ，求解中心点的公式直接参考论文即可，这里不讲怎么推导的。如果 C12 C 12 和 C34 C 34 之间的距离小于阈值 threcenter t h r e c e n t e r ，则其满足约束，否则不属于同一个椭圆。

        到这，弧段的约束有三个：象限约束、关联距离约束和邻近中心约束。

        根据上述的方法可以确定4条直线 l1,l2,l3,l4 l 1 , l 2 , l 3 , l 4 ，任意两个直线的交点理论上都是一个椭圆中心点。但是，由于不可避免的失真，交叉点通常分布在一个小范围内的确切中心。为了得到一个更好的结果，我们使用了7个点，分别是6个交点与 C12 C 12 和 C34 C 34 的中心点来估计椭圆中心点。理论上，误差越小，这7个点越密集，所以理论的中心点周围具有高密度的交点。传统方法是计算这7个点的中值作为其椭圆中心点，而作者则使用mean-shift 算法来找到高密度区域进而得到中心点坐标，进而提高了其对噪声的鲁棒性（mean-shift算法最近看见许多啊，但我不理解的是直接使用两个弧段上所有的点进行拟合会有很大误差吗？椭圆拟合算法还是很多的）。

3.3 参数估计

        这个小节阐述的是估计椭圆参数，完全用的是椭圆的拟合性质，没有看到拟合的内容，因为这个是计算椭圆参数，具体内容就可以直接看论文了，有需要的话我会详细重新推导一遍，这里就不细说（我还是不理解为啥不用拟合的方法→_→，可能用这个方法会很快地估计出椭圆参数吧）。

四 验证和聚类

4.1 候选椭圆的验证

用上面的方法得到椭圆仍然会存在一些虚假椭圆，验证方法能够进一步剔除错误椭圆。下面列出验证的两个要点。

• 长度比值的确认。 我们采用包围圆弧的包围盒的周长的一半和半轴长度之和的比率来测量椭圆周长。假设一个椭圆候选有一个弧段对 τ=(a1,a2) τ = ( a 1 , a 2 ) 拟合得到，这两个弧段的包围盒尺寸为 mi×ni,i=1,2 m i × n i , i = 1 , 2 ，椭圆半长短轴为 A,B A , B ，则长度比值的确认公式如下所示。这个值越大，说明越有效，如果 K(τ) K ( τ ) 大于阈值 threl t h r e l 则进入下一个验证条件。否则被认为是一个错误检测。这个条件的分数为 s(K(τ))=K(τ) s ( K ( τ ) ) = K ( τ ) 。

K(τ)=∑2i=1(mi+ni)2(A+B) K ( τ ) = ∑ i = 1 2 ( m i + n i ) 2 ( A + B )

• 通过周长比确认 这个条件的核心就是找到一对弧段中，有多少个像素点可以被认为是拟合出的椭圆上的点（通过距离判断，这里有个阈值 threφ t h r e φ ），在椭圆上的点与弧段所有的点的比值作为这个条件的分数 s(φ(τ))=φ(τ) s ( φ ( τ ) ) = φ ( τ )

4.2 椭圆聚类

        经过上述的验证，多个弧段几何可以被拟合为真椭圆，这些也有可能属于同一个椭圆。因此需要采用聚类的方法消除重复的椭圆。对于属于同一个椭圆的多弧段集合，最后采用分数最高的作为最终结果。

五 用于错误检测控制的几何性质

        这个是一个比较新的点子，这节我会详细进行翻译分析。

        由于椭圆的固有属性可以用数学模型来表达，作者开发了一个几何反馈回路来显著的消除错误检测。这里我们用下面的几何约束来描述椭圆的几何性质：设弦 Q1Q2 Q 1 Q 2 的中点是 QM Q M ，则斜率 kQ1Q2 k Q 1 Q 2 与 kQMO k Q M O 的乘积等于 −B2A2 − B 2 A 2 ，这个也就是中点弦公式（不禁想起了我7年前高考复习时常做的题目，233333，这个作者也萌萌哒的给出了证明步骤→_→）。

        验证是否满足这个性质作者叒提供了一个阈值 threp t h r e p （这里我的一个建议是，做论文不要整太多参数，算法敏感度很容易太高，而且调参做实验也麻烦，参数能自适应就自适应）。作者随机采了三对点，来验证结果，如果这些点满足这个集合约束，则接受检测，否则丢弃。

六 实验

        实验数据集这个作者又给补充了一个数据集 Dataset HX，是工业上的数据，目前还没有拿到数据，有的话我会更新上的。关于验证准则，数据集这里不多说，直接看结果。

        作者进行了参数灵敏度分析，还有仿真数据集的测试，这个非常好，以后做论文时候也要多多补充这点。

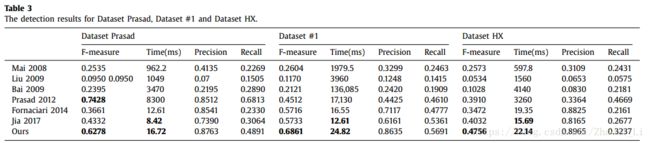
        下表示作者在三个数据及上测试得到的结果，有显著的提升，表明其方法的有效性，其提出的几何性质可以做未来学习的参考。同时我也放上了新数据集的检测而结果，效果也是可以的。

七 个人总结

        我个人觉得这篇文章，是基于之前14年Fornaciari和16年的文章的进一步改进，整合了这两个文章的优点，所以一定会比之前的要好。这篇文章的另一个中点在于其从各个检测步骤上都进行了严密仔细的加速，这以后也是个趋势。同时作者提出的基于几何的多种性质与方法都可以作为未来研究的参考。论文中的中点弦这个问题，其实我16年也想到了，但是当时因为其他问题导致结果不好，这篇文章也算是了却我心中一个问题。

        总之，Prasad的椭圆检测系列的文章非常适合新手去阅读，是入门的好文章，我会时刻关注他们的动态，以后有新的东西我会不断更新的。

---

---

1. 为了看算法的实际性能，我向原作者索要代码，作者回复说当他们处理完一些数据就会公开源码。所以等作者公开源码之后，我会补上这个链接的。. ↩
2. 这里的相关工作可以参考以前的椭圆检测文章，这里只是对之前工作的一个补充。 ↩
3. 分类到4个象限问题是14年Fornaciari的思想，论文为A fast and effective ellipse detector for embedded vision applications。 ↩
4. 使用mean-shift是16年Bae-Keun Kwon的思想。这篇文章我已经在博客中进行了分析椭圆检测 2016 Fast ellipse detection based on three point algorithm with edge angle information ↩
5. 弧段分割很重要，在保持精度的前提下能够提升计算速度很重要，但是最影响速度的在弧段分组，不在弧段分割。后期研究中，不要摆错了重点。 ↩
6. 图C所示的定理就是前面分析过的博客，16年的文章。 ↩