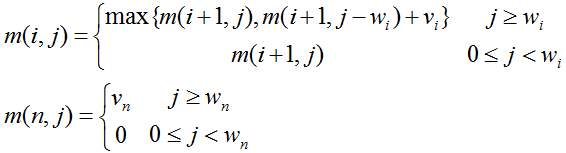算法 -- 0-1背包问题之动态规划

本来周五要完成0-1背包问题,由于自己的某些事情耽搁.以后要严格要求自己喽!!! 下面我们一起来学习0-1背包问题:

问题描述:
有N件物品和一个容量为c的背包。第i件物品的重量是w[i]，价值是v[i]。求解将哪些物品装入背包可使价值总和最大。之所以称为”0-1背包问题”表示该问题只有两种结果:装或者不装即0或者1.
基本思路:
该问题中,每一种物品只有一件,同时选择只有放和不放.
实现过程需要借助一个二维数组m[N+1][c+1],m[i][j]表示i号物品在容量为j时,放或者不放入时的最大价值.
我采用的是从最后一个物品开始分析,即从下至上分析.
首先给出一组数据:
总共物品数目:N=5 背包容量:c = 10
每个物品的重量w[6] = { 0 , 2 , 2 , 6 , 5 , 4 }
每个物品的价值v[6] = { 0 , 6 , 3 , 5 , 4 , 6 }
定义数组m[6][11]:

其中第0位，置为0，不参与计算，只是便于与后面的下标进行统一，无特别用处，也可不这么处理。因为物品总数为5,背包的最大容量为10，那么在设置数组m大小时，可以设行列值为6和11，那么，对于m(i,j)就表示可选物品为i…n背包容量为j(总重量)时背包中所放物品的最大价值。

过程分析:

1.首先背包初始是空的,任何一个物品都没有装入.

2.我们从最后一个物品开始分析,即在重量为0~10时,如何放置物品n,使其中价值最大,此时需要确定m[5][0~10]这11个元素的值.
如果物品的重量w[5]大于当前背包的剩余容量j,则背包不能放入该物品,即此时价值为m[5][j]=0;否则可以放入该物品,即此时价值为该物品的价值v[5].

3.接下来我们来分析前n-1个物品在j=0~10的情况下是否放入背包.此时每一个物品的分析都是建立在上一个物品的基础上的,以4号物品为例:
m[4][0~10]这11个值的确定,需要建立在5号物品的基础上.同样分为两种情况:第一种w[4]>j,则背包不能装入该物品,因此此时的最大价值为上一个物品的在j值下对应的值即m[4][j]=m[5][j];第二种w[4]<=j,则背包可以放入该物品,此时就需要比较放入后的价值大,还是不放的价值大.

4.和4号物品的分析方法一样,完成剩下的物品在m数组中的对应值.
总结来讲就是:
w[i]>j,则m[i][j]=m[i+1][j];
w[i]<=j, 则m[i][j]=max ( m[i+1][j] , v[i]+m[i+1][j-w[i]]).

以上内容综合起来表达如下图所示:

实现的代码如下:

/*************************************************************************
 **     >  Name : 0_1.c
 **     > Author: LiYingXiao (Sweethreart502) 
 **     >  Mail : [email protected]
 **     >  Blog : http://blog.csdn.net/u013166575
 **     > Created Time: 2015年11月21日 星期六 23时41分19秒
 ************************************************************************/

#include 

// 五个物品的对应重量
int w[6] = { 0 , 2 , 2 , 6 , 5 , 4 } ;
// 五个物品的对应价值
int v[6] = { 0 , 6 , 3 , 5 , 4 , 6 } ;
// 背包总容量
int c = 10 ;
// 每一个物品的状态值
int x[6] = { 0 } ;


// 核心处理函数
void process ( int m[][11] ) ;

// 输出放入情况
void option ( int m[][11] )  ;

int main ( int argc , char * argv[] )
{
    int i ;

    // 初始化价值数组为0
    int m[6][11] = { 0 } ;

    process ( m ) ;

    option ( m ) ;

    // 输出情况
    for ( i = 1 ; i <= 5 ; i++ ) {
        if ( x[i] ) {
            printf ( "1  " ) ;
        } else {
            printf ( "0  " ) ;
        }
    }
    printf ( "\n" ) ;

    return 0 ;
}

void process ( int m[][11] )
{
    int i , j ;

    /* 首先解决最后一个物品是否放入 */
    for ( j = 0 ; j <= c ; j++ ) {
        if ( w[5] > j ) {
            m[5][j] = 0 ; 
        } /* 不能放下,价值为零 */
        else {
            m[5][j] = v[5] ;
        }/* 可以放下,价值为其本身价值 */
    }

    /* 从下至上分析 */
    for ( i = 4 ; i >=  1 ; i-- ) { /* 从下至上依次分析每一个物品 */
        for ( j = 0 ; j <= c ; j++ ) { /* 从左至右一次分析j在0~10之间 */
            if ( w[i] > j ) { 
                m[i][j] = m[i+1][j] ;
            } /* 不能放入,则价值为下一行同一列的值 */
            else {
                m[i][j] = ( m[i+1][j] > v[i]+m[i+1][j-w[i]] ) ? m[i+1][j] : v[i]+m[i+1][j-w[i]] ;
                /* 如果放入,则它的价值为当前物品的价值加上下一个物品在剩余容量j减去当前物品重量的条件下的价值 */
            } /* 分析放入的价值大,还是不放的价值大 */
        }
    }
}

void option ( int m[][11] ) 
{
    int i , j = c ; 

    /* 初识情况将j设置为c总容量 */
    for ( i = 1 ; i <= 4 ; i++ ) {
        if ( m[i][j] == m[i+1][j] ) {
            /* 如果该物品价值与下一个物品在当前j下的价值相等,则该物品未放入.因为m数组初始情况是从下到上分析的 */
            x[i] = 0 ;
        } 
        else {
            x[i] = 1 ;
            j -= w[i] ; /* 放入某物品后,要将j减少该物品的重量 */
        }
    }
    /* 最后一个物品是否放入,只需要看当前物品在j下是否价值为零. */
    x[5] = m[5][j] ? 1 : 0 ;
} 

思考:
如果再添加一个约束条件总体积小于等于t,应该如何实现?

其实和二维的解决方法类似,就相当于数学上面的”同理可得”一样.

代码如下:

/*************************************************************************
 **     >  Name : wv_0_1.c
 **     > Author: LiYingXiao (Sweethreart502) 
 **     >  Mail : [email protected]
 **     >  Blog : http://blog.csdn.net/u013166575
 **     > Created Time: 2015年11月22日 星期日 09时32分45秒
 ************************************************************************/
/* 0_1问题的三维,即在两个约束条件的约束下 */
#include  
#include  
#include  
#include  
#include  
#include  

using namespace std;  

// 背包总容量
int c = 5 ;
// 背包总体积
int t = 10 ;
// 每一个物品的重量
int w[] = { 0 , 2 , 3 , 1 , 4 } ;  
// 每一个物品的体积
int s[] = { 0 , 4 , 5 , 7 , 8 } ;
// 每一个物品的价值
int v[] = { 0 , 8 , 3 , 2 , 4 } ;
// 物品的状态
int x[5];  


/* 0-1背包问题 */
void package0_1 ( int m[][11][11] )   
{  
    // 采用从底到顶的顺序来设置m[i][j][k]的值  
    int i , j , k ;
    // 首先分析最后一个物品
    for ( j = 0 ; j <= c ; j++ ) {
        for ( k = 0 ; k <= t ; k++ ) {
            if ( w[4] <= j && s[4] <= k ) {
                /* 重量和体积同时满足条件,则放入 */
                m[4][j][k] = v[4] ;
            } else {
                /* 任何一个不满足,则不放入 */
                m[4][j][k] = 0 ;
            }
        }
    }

    //对剩下的n-1个物品进行放置。  
    for( i = 3 ; i >= 1 ; i--) {
        for(int j = 0 ; j <= c ; j++) { 
            for ( k = 0 ; k <= t ; k++ ) {
                if ( w[i] <= j && s[i] <= k ) {
                    /* 重量和体积同时满足条件 */
                    m[i][j][k] = ( m[i+1][j][k] > v[i]+m[i+1][j-w[i]][k-s[i]] ) ? m[i+1][j][k] : v[i]+m[i+1][j-w[i]][k-s[i]] ;
                }
                else {
                    m[i][j][k] = m[i+1][j][k] ;
                }
            }
        }  
    }
}


void answer ( int m[][11][11] )
{  
    int i , j = c , k = t ;  

    // 遍历m数组,从第一个货物遍历,判断是否装入
    for ( i = 1 ; i <= 3 ; i++ ) { 
        if ( m[i][j][k] == m[i+1][j][k] ) { // 如果当前物品的价值与下一个物品价值相等,说明没有装i物品
            x[i] = 0;  
        }
        else { // 否则装进去
            x[i] = 1;  
            j = j - w[i];  
            k = k - s[i] ;
        }      
    }
    // 如果n物品在当前剩余容量j下非零,则表示装入该物品
    x[4] = m[i][j][k] ? 1 : 0 ;   
}

// 主函数
int main()  
{  
    // 5个物品,总重量为10,总体积为10
    // m数组分析中存储剩余空间为j时,当前的最大价值
    int m[5][11][11]={0};  // 初始化为0

    // 分析并存储m数组
    package0_1 ( m ) ;  


    // 具体的装载信息
    answer(m);  

    // 输出最优解
    cout << "The best answer is:\n";  
    for ( int i = 1 ; i <= 4 ; i++ ) { 
        cout << x[i] << " ";  
    }
    std::cout << std::endl ;

    return 0;  
}