排序算法总结及Python实现
目录
一、冒泡排序、选择排序和插入排序:O(n*n)
1、冒泡排序
2、选择排序
3、插入排序
二、归并排序和快速排序:O(nlogn)
1、归并排序
2、快速排序
三、桶排序和基数排序:O(n)
1、桶排序
2、基数排序
一、冒泡排序、选择排序和插入排序:O(n*n)
1、冒泡排序
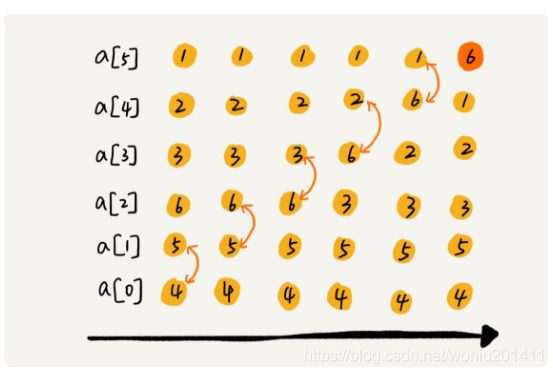
1、冒泡排序原理
冒泡排序对相邻的两个元素进行比较,看是否满足大小关系要求,如果不满足就让他俩交换,如下图所示。一次冒泡会让至少一个元素移动到它应该在的位置,重复n次,就完成n个数据的排序。
2、Python实现冒泡排序
from typing import List
def bubble_sort(a: List[int]):
length = len(a)
if length <= 1:
return
for i in range(length):
made_swap = False
for j in range(length - i - 1):
if a[j] > a[j + 1]:
a[j], a[j + 1] = a[j + 1], a[j]
made_swap = True
if not made_swap:
break3、冒泡排序性能分析
冒泡排序是稳定的排序算法。当相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序。
时间复杂度。最好的情况,数据有序,时间复杂度为O(n)。最坏的情况,时间复杂度为O(n*n)。平均情况,时间复杂度为O(n*n)。
空间复杂度。冒泡排序只涉及相邻数据的交换操作,时间复杂度为O(1)。
2、选择排序
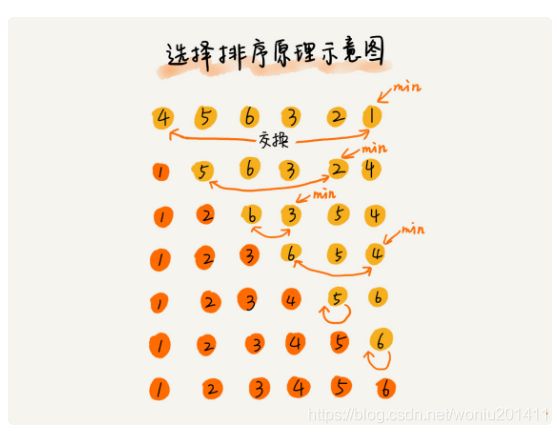
1、选择排序原理
选择排序分为已排序区间和未排序区间,每次从未排序区间中找到最小的元素,将其放到已排序区间的末尾。如下图所示:
2、Python实现选择排序
from typing import List
def selection_sort(a: List[int]):
length = len(a)
if length <= 1:
return
for i in range(length):
min_index = i
min_val = a[i]
for j in range(i, length):
if a[j] < min_val:
min_val = a[j]
min_index = j
a[i], a[min_index] = a[min_index], a[i]3、选择排序性能分析
选择排序不是稳定的排序算法。选择排序每次都要找未排序空间中最小值,并和前面的元素交换位置,破坏了稳定性。例如3,4,3,1
时间复杂度。最好情况、最坏情况和平均情况的时间复杂度都为O(n*n)。
空间复杂度。选择排序属于原地排序,空间复杂度为O(1)。
3、插入排序
1、插入排序原理
插入排序,将数组中的数据分为两个区间,已排序区间和未排序区间,初始已排序区间只有一个元素,就是数组的第一个元素。插入排序取未排序区间中的元素,在已排序区间中找到合适的位置将其插入,保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。如下图所示:
2、Python实现插入排序
from typing import List
def insertion_sort(a: List[int]):
length = len(a)
if length <= 1:
return
for i in range(1, length):
value = a[i]
j = i - 1
while j >= 0 and a[j] > value:
a[j + 1] = a[j]
j -= 1
a[j + 1] = value3、插入排序性能分析
插入排序是稳定的排序算法。对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现的元素后面,保持原有的前后顺序不变。
空间复杂度。插入排序是原地排序算法,时间复杂度为O(1)。
时间复杂度。最好情况,数组有序,不需要移动元素,时间复杂度为O(n)。最坏情况为O(n*n)。平均情况为O(n*n)。与冒泡排序相比,插入排序运行时间更少,因为每次移动元素,插入排序只需要1次赋值,而冒泡排序需要3次赋值才能交换元素。
二、归并排序和快速排序:O(nlogn)
1、归并排序
1、归并排序原理
归并排序的核心思想:如果排序一个数组,先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排序好的两部分合并在一起,这样整个数组就都有序了。如下图所示:
归并排序使用的分治思想,就是分而治之,将一个大问题分解成小的子问题来解决,一般用递归实现:
递推公式:
merge_sort(p..r) = merge(merge_sort(p..q), merge_sort(q+1..r))
终止条件:
p >= r 不用再继续分解2、python实现归并排序
from typing import List
def merge_sort(a: List[int]):
_merge_sort_between(a, 0, len(a)-1)
def _merge_sort_between(a: List[int], low: int, high: int):
if low < high:
mid = low + (high - low) // 2
_merge_sort_between(a, low, mid)
_merge_sort_between(a, mid+1, high)
_merge(a, low, mid, high)
def _merge(a: List[int], low: int, mid: int, high: int):
#a[low:mid],a[mid+1, high] are sorted
i, j = low, mid+1
tmp = []
while i <= mid and j <= high:
if a[i] <= a[j]:
tmp.append(a[i])
i += 1
else:
tmp.append(a[j])
j += 1
start = i if i <= mid else j
end = mid if i <= mid else high
tmp.extend(a[start: end + 1])
a[low:high+1] = tmp
if __name__ == "__main__":
a1 = [3, 6, 5, 8, 7]
merge_sort(a1)
print(a1)3、归并排序性能分析
归并排序是稳定的排序算法。归并排序稳定性关键要看merge函数,也就是两个有序子数组合并成一个有序数组,值相同的元素在合并时保持顺序不变。
时间复杂度。对n个元素进行归并排序需要的时间是T(n),那分解成两个子数组排序的时间是T(n/2),merge函数合并两个有序子数组的时间是n,T(n)的计算过程如下:
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2n
= 4*(2*T(n/8) + n/4) + 2n = 8*T(n/8) + 3n
= .....
= 2^k*T(n/2^k) + k*n当T(n/2^k)=T(1)时,k=logn, T(n)=n + n*logn。所以归并排序的时间复杂度为O(nlogn).
空间复杂度。归并排序在合并两个有序数组为一个有序数组时,需要借助额外的存储空间,空间复杂度为O(n).(在任意时刻,cpu只会有一个函数在执行,也就只会有一个临时的内存空间在使用)
2、快速排序
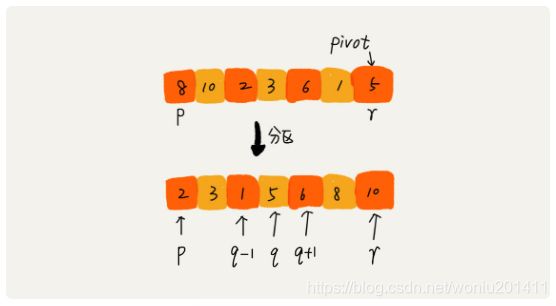
1、快排原理
快排核心思想:如果要排数组中下标从p到r之间的一组数据,我们选择p到r之间的任意一个数据为pivot(分区点)。遍历p到r之间的数据,将小于pivot的放到左边,大于pivot的放到右边,pivot放在中间。数组p到r之间的数据分成三个部分,前面p到q-1之间是小于pivot的,中间是pivot, 后面的q+1到r之间是大于pivot的。如下图所示:
快排利用的也是分治思想,可以用递归实现:
递推公式:
quick_sort(p..r) = quick_sort(p..q-1) + quick_sort(q+1..r)
终止条件:
p >= r2、python实现快速排序
from typing import List
import random
def quick_sort(a: List[int]):
_quick_sort_between(a, 0, len(a)-1)
def _quick_sort_between(a: List[int], low: int, high: int):
if low < high:
#get a random position as the pivot
k = random.randint(low, high) #防止数组有序,最坏情况发生
a[low], a[k] = a[k], a[low]
m = _partition(a, low, high)
_quick_sort_between(a, low, m-1)
_quick_sort_between(a, m+1, high)
def _partition(a: List[int], low: int, high: int):
pivot, j = a[low], low
for i in range(low+1, high+1):
if a[i] < pivot:
j += 1
a[j], a[i] = a[i], a[j]
a[low], a[j] = a[j], a[low]
return j
if __name__ == "__main__":
a1 = [4, 3, 2, 1]
quick_sort(a1)
print(a1)
a2 = [3, 4, 5, 6, 7]
quick_sort(a2)
print(a2)
a4 = [5, -1, 9, 3, 7, 8, 3, -2, 9]
quick_sort(a4)
print(a4)3、快速排序性能分析
快排不是稳定的排序算法。快排中遍历数组元素,将小于分区点的数放在左边,大于分区点的数放在右边。值相同元素的顺序会发生改变。
时间复杂度:最好的情况如同归并排序,时间复杂度为O(nlogn).最坏的情况,数组是有序的,时间复杂度为O(n^2).
空间复杂度:快排是原地排序算法,空间复杂度为O(1)。因而对大规模数据排序时,快排比归并排序更常用。
三、桶排序和基数排序:O(n)
1、桶排序
1、桶排序原理
桶排序核心思想,将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行快速排序,桶内排完序后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
2、桶排序性能分析
时间复杂度分析。如果要排序的数据有n个,我们把他们均匀地分到m个桶内,每个桶内有k=n/m个元素。每个桶内部使用快速排序,时间复杂度为O(k*logk),m个桶排序的时间复杂度为O(m*k*logk),因为k=n/m,所以整个桶的时间复杂度为O(n*log(n/m)).当桶的个数m接近数据个数n时,log(n/m)就是一个非常小的常量,桶排序的时间复杂度接近O(n).
3、适用场景
桶排序对要排序的数据非常苛刻。首先,要排序的数据需要容易地划分成m个桶,并且桶与桶之间有天然的大小顺序;其次,数据在各个桶之间的分布式比较均匀的。
桶排序比较适合用在外部排序中,数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载在内存中。例如,我们有10GB的订单数据,需要按照订单金额进行排序,但内存只有4G,无法一次性将10G数据都加载到内存中。可以借助桶排序解决这个问题:先扫描一遍文件,看订单金额的数据范围,假设最小是1元,最大是10万元;将所有订单根据金额划分到100个桶里,第一个桶我们存储金额在1元到1000元之内的订单,第二个桶存储金额在1001到2000元之内的订单,以此类推,每一个桶对应一个文件;理想情况,每个小文件大约100M的订单数据,我们可以将这100个小文件依次放到内存中,用快排来排序;所有小文件都排好序,我们只需要按照文件编号,从小到大依次读取每个小文件中的订单数据,并将其写入一个文件中,这个文件中存储的就是按照金额从小到大排序的订单数据。
2、基数排序
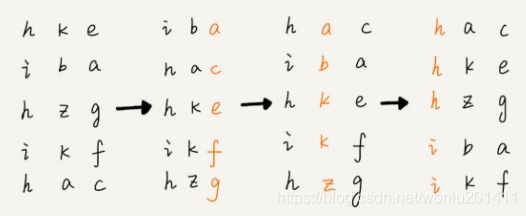
1、基数排序原理
基数排序按照每位来排序,排序算法需要是稳定的。如下图所示:
2、基数排序性能分析
时间复杂度。根据每一位来排序,可以用桶排序,时间复杂度为O(n),如果要排序的数据有k位,时间复杂度为O(k*n),k为常数时,基数排序的时间复杂度近似于O(n).
3、适用场景
要排序的数据可以分割出独立的位来比较,而且位之间有递进的关系,如果a数据的高位比b数据大,那剩下的地位就不用比较了。
总结:
|
|
稳定性 |
空间复杂度 |
最好 |
最坏 |
平均 |
| 冒泡排序 |
稳定 |
O(1) |
O(n) |
O(n*n) |
O(n*n) |
| 插入排序 |
稳定 |
O(1) |
O(n) |
O(n*n) |
O(n*n) |
| 选择排序 |
不稳定 |
O(1) |
O(n*n) |
O(n*n) |
O(n*n) |
| 归并排序 |
稳定 |
O(n) |
O(nlogn) |
O(nlogn) |
O(nlogn) |
| 快速排序 |
不稳定 |
O(1) |
O(nlogn) |
O(n*n) |
O(nlogn) |
| 桶排序 |
稳定 |
O(n) |
O(n) |
||
| 基数排序 |
稳定 |
O(n) |
O(n) |
参考资料:
极客时间:《数据结构与算法之美》