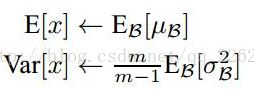目标检测部分知识点总结
目录
- 一、focal loss:
- 二、bounding box regression
- 三、IoU计算
- 四、NMS(non-maximum suppression,非极大值抑制)
- 五、yolov3的loss
-
- 1. conf和cls的bce loss(Binary cross-entropy loss)
- 2. 候选框回归的MSE loss
- 3. 最终loss
- 六、交叉熵损失函数(cross-entropy loss)
- 七、Faster RCNN的loss
- 八、RoI Align和RoI Pool
- 九、batch normalization批标准化
一、focal loss:
p t = { p if y=1 1 − p o t h e r w i s e , α t = { α y = 1 1 − α y = − 1 p_t=\begin{cases} p & \text{if y=1} \\ 1-p & otherwise, \end{cases}\\ \alpha_t=\begin{cases} \alpha & y=1 \\ 1-\alpha & y=-1 \end{cases}\\ pt={ p1−pif y=1otherwise,αt={ α1−αy=1y=−1
平衡正负例:
C E ( p t ) = − α t log p t CE(p_t)=-\alpha_t\log{p_t} CE(pt)=−αtlogpt
平衡难易例:
F L ( p t ) = − ( 1 − p t ) γ log p t FL(p_t)=-(1-p_t)^\gamma \log{p_t} FL(pt)=−(1−pt)γlogpt
总体公式:
F L ( p t ) = − α t ( 1 − p t ) γ log p t FL(p_t)=-\alpha_t(1-p_t)^\gamma \log{p_t} FL(pt)=−αt(1−pt)γlogpt
(论文中 γ = 2 , α = 0.25 \gamma=2, \alpha=0.25 γ=2,α=0.25效果最好)
二、bounding box regression
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t h b_x=\sigma(t_x)+c_x \\ b_y=\sigma(t_y)+c_y \\ b_w=p_w e^{t_w} \\ b_h=p_h e^{t_h} bx=σ(tx)+cxby=σ(ty)+cybw=pwetwbh=pheth
其中 t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th分别为网络的输出, c x , c y c_x, c_y cx,cy分别是锚框中心点的坐标, b x , b y , b w , b h b_x, b_y, b_w, b_h bx,by,bw,bh分别是最终得到锚框的中心点坐标和宽高, p w , p h p_w, p_h pw,ph是设定的锚框的宽高(在yolov3中设定了9组不同的宽高)
在yolov3中的候选框回归代码如下:
x = torch.sigmoid(prediction[..., 0]) # Center x
y = torch.sigmoid(prediction[..., 1]) # Center y
w = prediction[..., 2] # Width
h = prediction[..., 3] # Height
pred_boxes[..., 0] = x.data + self.grid_x
pred_boxes[..., 1] = y.data + self.grid_y
pred_boxes[..., 2] = torch.exp(w.data) * self.anchor_w
pred_boxes[..., 3] = torch.exp(h.data) * self.anchor_h
三、IoU计算
I o U = I n t e r s e t i o n _ a r e a / U n i o n _ a r e a IoU=Intersetion\_area/Union\_area IoU=Intersetion_area/Union_area
为了求解Intersetion_area也就是相交区域面积,需要知道相交区域的左上角和右下角的坐标。
计算方式如下:
# 左上角
inter_rec_x1 = torch.max(b1_x1, b2_x1)
inter_rec_y1 = torch.max(b1_y1, b2_y1)
# 右下角
inter_rec_x2 = torch.min(b1_x2, b2_x2)
inter_rec_y2 = torch.min(b1_y2, b2_y2)
之后再利用长乘宽的方式求面积即可。需要注意的是 宽 = x 2 − x 1 + 1 宽=x_2-x_1+1 宽=x2−x1+1,这个+1不能忘,最后那个相并区域因为是分母,为了防止出现分母为0的错误,需要加上1e-16。
总体代码如下:
def bbox_iou(box1, box2, x1y1x2y2 = True):
# xywh->xyxy
if not x1y1x2y2:
# 别忘了给w、h除2
b1_x1, b1_x2 = box1[:, 0]-box1[:, 2]/2, box1[:, 0]+box1[:, 2]/2
b1_y1, b1_y2 = box1[:, 1]-box1[:, 3]/2, box1[:, 1]+box1[:, 3]/2
b2_x1, b2_x2 = box2[:, 0] - box2[:, 2] / 2, box2[:, 0] + box2[:, 2] / 2
b2_y1, b2_y2 = box2[:, 1] - box2[:, 3] / 2, box2[:, 1] + box2[:, 3] / 2
else:
b1_x1, b1_y1, b1_x2, b1_y2 = box1[:, 0], box1[:, 1], box1[:, 2], box1[:, 3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[:, 0], box2[:, 1], box2[:, 2], box2[:, 3]
inter_rec_x1 = torch.max(b1_x1, b2_x1)
inter_rec_x2 = torch.min(b1_x2, b2_x2)
inter_rec_y1 = torch.max(b1_y1, b2_y1)
inter_rec_y2 = torch.min(b1_y2, b2_y2)
# 利用clamp函数将最小值设置为0,防止出现错误hanshu
inter_area = torch.clamp(inter_rec_x2-inter_rec_x1+1, min=0)* \
torch.clamp(inter_rec_y2-inter_rec_y1+1, min=0)
b1_area = (b1_x2-b1_x1+1)*(b1_y2-b1_y1+1)
b2_area = (b2_x2-b2_x1+1)*(b2_y2-b2_y1+1)
# 分母加上1e-16来避免分母为0的情况
# iou = 相交/相并
iou = inter_area/(b1_area+b2_area-inter_area+1e-16)
return iou
四、NMS(non-maximum suppression,非极大值抑制)
NMS的步骤如下:
- 将所有conf值不超过conf_thres的框删去
- 求得所有框的分数(conf值*最大的cls pred值)
- 将所有框按照框的分数由大到小排序
- 取出分数最大框,计算该框与所有框IoU,如果该框与某个框IoU大于nms_thres且该框与某个框的类别标签一致,那么就删去那个框,同时将分数最大框保留,放入keep_boxes中。
- 一直重复第4步,直到删除完毕所有框
- 如果keep_boxes不为空的话,那么将keep_boxes放入当前图片的输出结果output[image_i]中。
代码如下(代码是自己写的,所以如果有错误请指正)
def xywh2xyxy(box):
result = box.new(box.shape)
result[..., 0], result[..., 2] = box[:, 0] - box[:, 2] / 2, box[:, 0] + box[:, 2] / 2
result[..., 1], result[..., 3] = box[:, 1] - box[:, 3] / 2, box[:, 1] + box[:, 3] / 2
return result
def NMS(prediction, conf_thres=0.5, nms_thres=0.4):
prediction[..., :4] = xywh2xyxy(prediction[..., :4])
output = [None for _ in range(len(prediction))]
for image_i, image_pred in enumerate(prediction):
# conf < conf_thres的框全部删去
image_pred = image_pred[image_pred[:, 4] >= conf_thres]
if not image_pred.size(0):
continue
# 计算分数
score = image_pred[:, 4]*image_pred[:, 5:].max(1)[0]
# 根据分数排序
image_pred = image_pred[(-score).argsort()]
# 求出每个框的类别
class_preds =image_pred[:, 5:].max(1, keepdim=True)[1]
detections = torch.cat((image_pred, class_preds.float()), 1)
keep_boxes = []
while detections.size(0):
# unsqueeze(0)扩充出第0维,求iou,与当前框iou大于nms_thres的框位置为True
large_overlap = bbox_iou(detections[0, :4].unsqueeze(0), detections[:, :4]) > nms_thres
# 与当前框的label相同的框的位置为True
label_match = detections[0, -1] == detections[:, -1]
invalid = large_overlap&label_match
# 将当前最大score的框放入keep_boxes中
keep_boxes += [detections[0][:-1]]
# 删除所有invalid为True的框
detections = detections[~invalid]
if keep_boxes:
# 将keep_boxes放入当前图像的output[image_i]
output[image_i] = torch.stack(keep_boxes)
return output
五、yolov3的loss
1. conf和cls的bce loss(Binary cross-entropy loss)
# 计算conf和cls
pred_conf = torch.sigmoid(prediction[..., 4])
pred_cls = torch.sigmoid(prediction[..., 5:])
# 计算loss
self.bce_loss = nn.BCELoss()
loss_conf_obj = self.bce_loss(pred_conf[obj_mask], tconf[obj_mask])
loss_conf_noobj = self.bce_loss(pred_conf[noobj_mask], tconf[noobj_mask])
loss_conf = self.obj_scale * loss_conf_obj + self.noobj_scale * loss_conf_noobj
loss_cls = self.bce_loss(pred_cls[obj_mask], tcls[obj_mask])
公式:
l o s s ( X i , y i ) = − w i [ y i log x i + ( 1 − y i ) log ( 1 − x i ) ] loss(X_i, y_i)=-w_i[y_i\log{x_i}+(1-y_i)\log{(1-x_i)}] loss(Xi,yi)=−wi[yilogxi+(1−yi)log(1−xi)]
2. 候选框回归的MSE loss
在yolov3中,候选框回归的loss为mse loss,对应的代码为:
self.mse_loss = nn.MSELoss()
loss_x = self.mse_loss(x[obj_mask], tx[obj_mask])
loss_y = self.mse_loss(y[obj_mask], ty[obj_mask])
loss_w = self.mse_loss(w[obj_mask], tw[obj_mask])
loss_h = self.mse_loss(h[obj_mask], th[obj_mask])
MSE loss的公式为:
J = 1 2 ( y i − y i ^ ) 2 J=\frac{1}{2}(y_i-\hat{y_i})^2 J=21(yi−yi^)2
3. 最终loss
t o t a l l o s s = l o s s x + l o s s y + l o s s w + l o s s h + l o s s c o n f + l o s s c l s total_loss = loss_x + loss_y + loss_w + loss_h + loss_{conf} + loss_{cls} totalloss=lossx+lossy+lossw+lossh+lossconf+losscls
六、交叉熵损失函数(cross-entropy loss)
l o s s ( X i , y i ) = − w l a b e l log e x l a b e l ∑ j = 1 N e x j loss(X_i, y_i)=-w_{label}\log{\frac{e^{x_{label}}}{\sum_{j=1}^N{e^{x_j}}}} loss(Xi,yi)=−wlabellog∑j=1Nexjexlabel
七、Faster RCNN的loss
L ( p i , t i ) = 1 N c l s ∑ i L c l s ( p i , p i ∗ ) + λ 1 N r e g ∑ i p i ∗ L r e g ( t i , t i ∗ ) L({p_i},{t_i})=\frac{1}{N_{cls}}\sum_i{L_{cls}(p_i, p_i^*)}\\ +\lambda\frac{1}{N_{reg}}\sum_i{p_i^*L_{reg}(t_i, t_i^*)} L(pi,ti)=Ncls1i∑Lcls(pi,pi∗)+λNreg1i∑pi∗Lreg(ti,ti∗)
其中 p i p_i pi是第i个锚框为目标的网络输出概率, p i ∗ p_i^* pi∗是该锚框真值, t i t_i ti是网络输出的锚框的4个信息(参考本文第二部分), t i ∗ t_i^* ti∗是真值框的信息。 L c l s L_{cls} Lcls是log loss, L r e g L_{reg} Lreg是robust loss function(smooth L1), L r e g ( t i , t i ∗ ) = R ( t i − t i ∗ ) L_{reg}(t_i, t_i^*)=R(t_i-t_i^*) Lreg(ti,ti∗)=R(ti−ti∗)。 p i ∗ L r e g p_i^*L_{reg} pi∗Lreg代表着只有在锚框有物体时才会有第二部分的回归框loss。 N c l s , N r e g N_{cls}, N_{reg} Ncls,Nreg分别是mini-batch的大小和锚框位置的个数,用于归一化。 λ \lambda λ是平衡系数。
s m o o t h L 1 ( x ) = { 0.5 x 2 i f ∣ x ∣ < 1 ∣ x ∣ − 0.5 o t h e r w i s e , smooth_{L_1}(x)=\begin{cases} 0.5x^2 & if |x|<1 \\ |x|-0.5 & otherwise, \end{cases} smoothL1(x)={ 0.5x2∣x∣−0.5if∣x∣<1otherwise,
L c l s = − ( y log ( p ) + ( 1 − y ) log ( 1 − p ) ) L_{cls}=-(y\log{(p)}+(1-y)\log{(1-p)}) Lcls=−(ylog(p)+(1−y)log(1−p))
八、RoI Align和RoI Pool
参考Mask RCNN整体介绍及部分细节讲解一文的第三部分。
九、batch normalization批标准化
将每层数据转化为标准正态分布的偏移缩放来解决梯度消失的问题。
训练时:

此处的 μ B \mu_B μB和 σ B 2 \sigma_B^2 σB2为mini-batch的均值和方差。
测试时:
使用的 μ B \mu_B μB和 σ B 2 \sigma_B^2 σB2为训练集全局的均值和方差。