CNN改进：Drop an Octave Reducing Spatial Redundancy in CNN - Octave Convolution论文解析
1.Comprehensive narrative（综述部分）
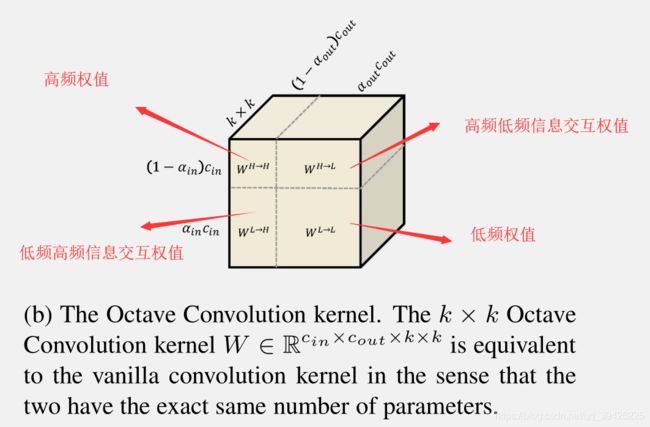
首先这篇paper主要是将普通的CNN卷积特征图分为两个部分 还有就是将convolution kernel分为4个部分
（1）首先卷积特征图被分为两个部分：如下图=-=
- 高空间频率部分卷积（也就是图像的边缘和轮廓）
- 低空间频率部分卷积（也就是强度综合部分）
（2）卷积核的四个部分：如下图=-=
（3）补充一下频率方面的知识 PS：=-= 其实都是现用现学啊哈~~
简单一点说，图像中的高频分量，指的是图像强度（亮度/灰度）变化剧烈的地方，也就是我们常说的边缘（轮廓）；图像中的低频分量，指的是图像强度（亮度/灰度）变换平缓的地方，也就是大片色块的地方。 人眼对图像中的高频信号更为敏感，举个例子，在一张白纸上有一行字，那么我们肯定直接聚焦在文字上，而不会太在意白纸本身，这里文字就是高频信号，而白纸就是低频信号。
如下图：啊哈，同学是不是找到了最上面两张图片的频率图 - Form:知 乎：Heinrich
咳咳。。。。。（一开说就飚不住自己）下面进入paper正文了 - _ -!!
2.Abstract (摘要部分)
在作者的paper里，他的Octave Convolution 有下面几条优点：
- 对混合特征图进行频率分解，设计了他的(OctConv)来存储和处理空间变化的特征图，对于较低在较低的空间分辨率通过对图片的缩放减少了内存和计算成本。
- OctConv被定义为一个单一的、通用的、即插即用的卷积单元，它可以作为(普通的)卷积的直接替换，而无需对网络体系结构进行任何调整。
原文如下-----------》
In this work, we propose to factorize the mixed feature maps by their frequencies, and design a novel Octave Convolution (OctConv) operation 1 to store and process feature maps that vary spatially “slower” at a lower spatial resolution reducing both memory and computation cost. Unlike existing multi-scale methods, OctConv is formulated as a single, generic, plug-and-play convolutional unit that can be used as a direct replacement of (vanilla) convolutions without any adjustments in the network architecture. It is also orthogonal and complementary to methods that suggest better topologiesor reduce channel-wise redundancy like group or depth-wise convolutions. We experimentally show that by simply replacing convolutions with OctConv.
最后当然实现了牛批的操作：
- 提高了图片和视频重建任务的精度。
- 减少了卷积核的占用内存和计算消耗。
3.Introduction（引言部分）
PS：前面的吧啦吧啦大家自己看吧，就说一说他们贡献
- 他们讲特征图分为高低频两个部分并用不同的卷积处理他们。so，低频图可以被咔嚓掉一部分，所以就减少了内存和计算成本。重点，重点，重点，这就可以理解为你增加了感受野的范围就可以捕捉到更多的神奇宝贝（上下文信息）。
- 第二就是他们的即插即用，单一的什么的吧啦吧啦
- 第三就是在很多领域取得了很大的效果和成就
4.Octave Feature Representation
let X ∈ R c × h × w R^{c×h×w} Rc×h×w denote the input feature tensor of a convolutional layer, where h and w denote the spatial dimensions and c the number of feature maps or channels. We explicitly factorize X along the channel dimension into X = { X H X^H XH, X L X^L XL }, where the high-frequency feature maps X H X^H XH∈ R ( 1 − α ) c × h × w R^{(1−α)c×h×w} R(1−α)c×h×w capture fine details and the low frequency maps X L ∈ R α c × h / 2 × w / 2 X^L ∈ R^{αc×h/2 × w/2} XL∈Rαc×h/2×w/2 vary slower in the spatial dimensions (w.r.t. the image locations). Here α ∈ [0,1] denotes the ratio of channels allocated to the low-frequency part and the low-frequency feature maps are defined an octave lower than the high frequency ones
解释一下就是他将输入卷积核的特征张量按照α 的比列分成两部分卷积
1、高频特征张量的维度是（1-α ）乘以 图片的高度 乘以 图片的宽度
2、低频特征张量的维度是 α 乘以 图片的高度 乘以 图片的宽度 ！ =-=如下图：
5.Octconv
1.下面是我们普通的卷积层计算公式：
Y p , q = ∑ i , j ∈ N K W i + ( k − 1 / 2 ) , j + ( k − 1 / 2 ) ⊺ X p + i , q + i ( 1 ) Y_{p,q}=\sum_{i,j\in N_K} W_{i+(k-1/2),j+(k-1/2)} \intercal X_{p+i,q+i} \quad\quad(1) Yp,q=i,j∈NK∑Wi+(k−1/2),j+(k−1/2)⊺Xp+i,q+i(1)
Vanilla Convolution. Let W ∈ R c × k × k R^{c×k×k} Rc×k×k denote a k × k convolution kernel and X,Y ∈ R c × h × w R ^{c×h×w} Rc×h×w denote the input and output tensors,respectively. Each featuremap in Y p , q Y_{p,q} Yp,q∈ R c R^c Rc can be computed by eq.(1)
where (p,q) denotes the location coordinate and N k N_k Nk =
{ ( i , j ) : i = { ( − k − 1 ) / 2 , . . . , ( k − 1 ) / 2 } , j = { ( − k − 1 ) / 2 , . . . , ( k − 1 ) / 2 } } \{(i,j) : i = \{(− k−1)/ 2 ,..., (k−1)/ 2 \},j = \{(− k−1)/ 2 ,..., (k−1)/ 2 \}\} { (i,j):i={ (−k−1)/2,...,(k−1)/2},j={ (−k−1)/2,...,(k−1)/2}}defines a local neighborhood. For simplicity, in all equations we omit the padding, we assume k is an odd number and that the input and output data have the same dimensionality, i.e. c in = c out = c.
解释：这就代表平常卷积核的计算 W吧啦吧啦是卷积核的权重矩阵， X吧啦吧啦代表是张量矩阵。怎么说呢， N k N_k Nk我感觉代表是卷积核卷积过程感受野除中心外周围旁边的权重小方块
2.OctConv的卷积计算公式：
很清晰，1.高频输出是低频与高频交互后的信息加上高频信息
2.低频输出是高频与低频交互后的信息加上低频信息
（1）高频输出：
解释：这么说吧， Y p , q H Y_{p,q}^H Yp,qH代表的就是高频p，q坐标位置的卷积输出等于高频本身的权重矩阵乘以他的高频特征张量矩阵 X H X^H XH加上低高频交互权重矩阵乘以低频特征张量矩阵 X L X^L XL
PS：因为低频特征图被咔嚓掉了一半，所以低频特征图对应坐标也会缩小一半才能指向意义相同的两个点，[ ]代表的是向下取整
（2）低频输出：
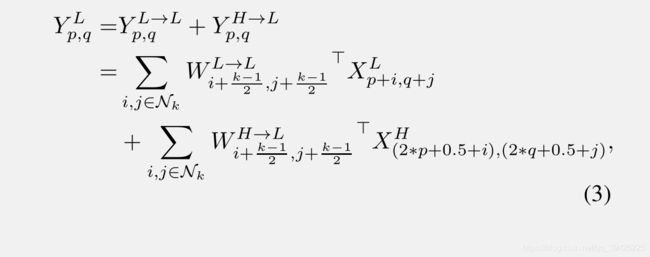
解释：这么说吧， Y p , q L Y_{p,q}^L Yp,qL代表的就是低频p，q坐标位置的卷积输出等于低频本身的权重矩阵乘以他的低频特征张量矩阵 X L X^L XL加上低高频交互权重矩阵乘以低频特征张量矩阵 X H X^H XH
PS：因为低频特征图被咔嚓掉了一半，所以高频特征图对应低频坐标必须扩大两倍才能指向意义相同的两个。至于那个0.5是为了防止misalignment,将2乘以位置(p, q)进行向下采样，并进一步将位置移动半步，以确保向下采样的映射与输入保持良好的对齐。然而，由于 X H X^{H} XH的索引只能是一个整数，我们可以将索引四舍五入到(2 * p+i, 2 * q+j)，或者通过对所有4个相邻位置求平均值来近似(2 * p+0.5+i, 2 * q+0.5+j)
6.Implementation Details（conv输出的实现）
这里其实很简单就是重采样和pooling，如下图：
这里展示了使用了高低频的效果，如下图：
