最小二乘法Python的实现

最小二乘法Python的实现

BY:Yang Liu
代码和解析：
import numpy as np ——载入numpy库，相当于增加矩阵数组容器
import scipy as sp ——载入scipy库，为科学计算算法库
import matplotlib.pyplot as plt ——载入matplotlib库，增加绘图库，若再载入Pandas库（相当于表格库），此时Python可实现MATLAB的功能
from scipy.optimize import leastsq ——从scipy中调用leastsq(最小二乘法算法)函数
Xi=np.array([7.66,2.71,8.29,7.91,5.67,2,5.98,1.5,9.8,4.7]) ——输入数据，转换成数组形式
Yi=np.array([5.33,2.88,10.41,6.1,5.31,4.26,6,1.4,10,5.3])
def func(p,x): ——定义函数func;p,x表示函数参数，此为确定最终拟合曲线的类型
k,b=p
return kx+b
def error(p,x,y): ——定义函数error,参数为p,x,y;此为偏差函数，为leastsq函数的输入值
return func(p,x)-y
p0=[1,20] ——此为函数参数的初始值，可为任意值
Para=leastsq(error,p0,args=(Xi,Yi)) ——error代表偏差函数；p0表示拟合函数的参数；第三个数据表示测得的原始数据值，为tuple元组形式，所以此处用args函数转换原始数据为元组形式
k,b=Para[0] ——leastsq函数的返回值第一项为函数参数
print(“k=”,k,“b=”,b) ——输出参数
print(“cost：”+str(Para[1])) ——输出leastsq函数的第二个参数
print(“求解的拟合直线为:”)
print(“y=”+str(round(k,2))+“x+”+str(round(b,2))) ——输出最终曲线函数
plt.figure(figsize=(8,6)) ——绘图，设置图形尺寸为4：3
plt.scatter(Xi,Yi,color=“green”,label=“样本数据”,linewidth=2) ——绘制散点图，scatter为绘制散点图函数，linewidth标定线宽
x=np.linspace(0,12,100) ——在0——12区间取100个点
y=kx+b
plt.plot(x,y,color=“red”,label=“拟合直线”,linewidth=2) ——绘制拟合曲线
plt.legend(loc=‘lower right’) ——设定图例说明位置
plt.show()
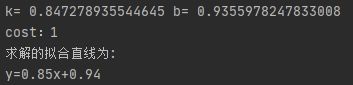
输出结果：