TensorFlow 2.0深度学习算法实战 第三章 分类问题

在人工智能上花一年时间，这足以让人相信上帝的存在。−艾伦·佩利

前面已经介绍了用于连续值预测的线性回归模型，现在我们来挑战分类问题。分类问题的一个典型应用就是教会机器如何去自动识别图片中物体的种类。考虑图片分类中最简单的任务之一：0~9 数字图片识别，它相对简单，而且也具有非常广泛的应用价值，比如邮政编码、快递单号、手机号码等都属于数字图片识别范畴。我们将以数字图片识别为例，探索如何用机器学习的方法去解决这个问题。

3.1 手写数字图片数据集

机器学习需要从数据中间学习，首先我们需要采集大量的真实样本数据。以手写的数字图片识别为例，如图 3.1 所示，我们需要收集大量的由真人书写的 0~9的数字图片，为了便于存储和计算，一般把收集的原始图片缩放到某个固定的大小(Size 或 Shape)，比如224 个像素的行和 224 个像素的列(224 × 224)，或者 96 个像素的行和 96 个像素的列(96 × 96)，这张图片将作为输入数据 x。

同时，我们需要给每一张图片标注一个标签(Label)，它将作为图片的真实值，这个标签表明这张图片属于哪一个具体的类别，一般通过映射方式将类别名一一对应到从 0 开始编号的数字，比如说硬币的正反面，我们可以用0 来表示硬币的反面，用 1 来表示硬币的正面，当然也可以反过来 1 表示硬币的反面，这种编码方式叫作数字编码(Number Encoding)。对于手写数字图片识别问题，编码更为直观，我们用数字的 0~9 来表示类别名字为 0~9 的图片。

如果希望模型能够在新样本上也能具有良好的表现，即模型泛化能力(GeneralizationAbility)较好，那么我们应该尽可能多地增加数据集的规模和多样性(Variance)，使得我们用于学习的训练数据集与真实的手写数字图片的分布(Ground-truth Distribution)尽可能的逼近，这样在训练数据集上面学到了模型能够很好的用于未见过的手写数字图片的预测。

为了方便业界统一测试和评估算法， (Lecun, Bottou, Bengio, & Haffner, 1998)发布了手写数字图片数据集，命名为 MNIST，它包含了 0~9 共 10 种数字的手写图片，每种数字一共有 7000 张图片，采集自不同书写风格的真实手写图片，一共 70000 张图片。其中 60000张图片作为训练train(Training Set)，用来训练模型，剩下 10000 张图片作为测试集test(Test Set)，用来预测或者测试，训练集和测试集共同组成了整个 MNIST 数据集。

考虑到手写数字图片包含的信息比较简单，每张图片均被缩放到28 × 28的大小，同时只保留了灰度信息，如图 3.2 所示。这些图片由真人书写，包含了如字体大小、书写风格、粗细等丰富的样式，确保这些图片的分布与真实的手写数字图片的分布尽可能的接近，从而保证了模型的泛化能力。

现在我们来看下图片的表示方法。一张图片包含了ℎ行(Height/Row)，列(Width/Column)，每个位置保存了像素(Pixel)值，像素值一般使用 0~255 的整形数值来表达颜色强度信息，例如 0 表示强度最低，255 表示强度最高。如果是彩色图片，则每个像素点包含了 R、G、B 三个通道的强度信息，分别代表红色通道、绿色通道、蓝色通道的颜色强度，所以与灰度图片不同，它的每个像素点使用一个 1 维、长度为 3 的向量(Vector)来表示，向量的 3 个元素依次代表了当前像素点上面的 R、G、B 颜色强值，因此彩色图片需要保存为形状是[ℎ, , 3]的张量(Tensor，可以通俗地理解为 3 维数组)。如果是灰度图片，则使用一个数值来表示灰度强度，例如 0 表示纯黑，255 表示纯白，因此它只需要一个形为[ℎ, ]的二维矩阵(Matrix)来表示一张图片信息(也可以保存为[ℎ, , 1]形状的张量)。

图 3.3 演示了内容为 8 的数字图片的矩阵内容，可以看到，图片中黑色的像素用 0 表示，灰度信息用 0~255 表示，图片中灰度越白的像素点，对应矩阵位置中数值也就越大。

目前常用的深度学习框架，如 TensorFlow，PyTorch 等，都可以非常方便的通过数行代码自动下载、管理和加载 MNIST 数据集，不需要我们额外编写代码，使用起来非常方便。我们这里利用TensorFlow 自动在线下载 MNIST 数据集，并转换为 Numpy 数组格式：

import os
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,optimizers,datasets

(x,y),(x_val,y_val)=datasets.mnist.load_data()#60000训练集/10000测试集
x=2*tf.convert_to_tensor(x,dtype=tf.float32)/255-1 #转换为张量，缩放到-1~1 60000*28*28
y=tf.one_hot(y,depth=10)#one-hot编码  60000,10
print(x.shape,y.shape)
train_dataset=tf.data.Dataset.from_tensor_slices((x,y))#构建数据集对象
train_dataset=train_dataset.batch(512)#批量训练

load_data()函数返回两个元组(tuple)对象，第一个是训练集，第二个是测试集，每个 tuple的第一个元素是多个训练图片数据$X$，第二个元素是训练图片对应的类别数字$Y$。其中训练集$X$的大小为(60000,28,28)，代表了 60000 个样本，每个样本由 28 行、28 列构成，由于是灰度图片，故没有 RGB 通道；训练集$Y$的大小为(60000, )，代表了这 60000 个样本的标签数字，每个样本标签用一个 0~9 的数字表示。测试集 $X$ 的大小为(10000,28,28)，代表了10000 张测试图片，$Y$ 的大小为(10000, )。

从 TensorFlow 中加载的 MNIST 数据图片，数值的范围在[0,255]之间。在机器学习中间，一般希望数据的范围在 0 周围小范围内分布。通过预处理步骤，我们把[0,255]像素范围归一化(Normalize)到[0,1.]区间，再缩放到[−1,1]区间，从而有利于模型的训练。

每一张图片的计算流程是通用的，我们在计算的过程中可以一次进行多张图片的计算，充分利用 CPU 或 GPU 的并行计算能力。一张图片我们用 shape 为[h, w]的矩阵来表示，对于多张图片来说，我们在前面添加一个数量维度(Dimension)，使用 shape 为[, ℎ, ]的张量来表示，其中的代表了 batch size(批量)；多张彩色图片可以使用 shape 为[, ℎ, , ]的张量来表示，其中的表示通道数量(Channel)，彩色图片 = 3。通过 TensorFlow 的Dataset 对象可以方便完成模型的批量训练，只需要调用 batch()函数即可构建带 batch 功能的数据集对象。

3.2 模型构建

回顾我们在回归问题讨论的生物神经元结构。我们把一组长度为$d_{in}$的输入向量 =[1, 2, … , ]简化为单输入标量 x，模型可以表达成 = ∗ + 。如果是多输入、单输出的模型结构的话，我们需要借助于向量形式：
$$y={\mathbf{w}}^T\mathbf{x}+b=\left[w_1,w_2,w_3,\dots ,w_{d_{in}}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ \dots \\ x_{d_{in}}\end{array}\right]+b$$
更一般地，通过组合多个多输入、单输出的神经元模型，可以拼成一个多输入、多输出的模型：
$$y=Wx+b$$
其中，$\mathbf{x}\in R^{d_{in}},\mathbf{b}\in R^{d_{out}},\mathbf{y}\in R^{d_{out}},W\in R^{d_{out}\times d_{in}}$

对于多输出节点、批量训练方式，我们将模型写成张量形式：
$$Y=X@W+b$$
其中$X\in R^{b\times d_{in}},\mathbf{b}\in R^{d_{out}},Y\in R^{b\times d_{out}},W\in R^{d_{in}\times d_{out}}$，$d_{in}$表示输入节点数，$d_{out}$表示输出节点数；$X$ shape 为[, $d_{in}$]，表示个样本的输入数据，每个样本的特征长度为；$W$的 shape 为[$d_{in}$,$d_{out}$]，共包含了$d_{in}$*$d_{out}$个网络参数；偏置向量 shape 为$d_{out}$，每个输出节点上均添加一个偏置值；@符号表示矩阵相乘(Matrix Multiplication，matmul)。

考虑 2 个样本，输入特征长度$d_{in}$= 3，输出特征长度$d_{out}$= 2的模型，公式展开为
$$\left[\begin{array}{cc}{o}_1^1& o_2^1\\ o_1^2& o_2^2\end{array}\right]=\left[\begin{array}{ccc}{x}_1^1& x_2^1& x_3^1\\ x_1^2& x_2^2& x_3^2\end{array}\right]\left[\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\\ w_{31}& w_{32}\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]$$
其中$x_1^1$, $o_0^0$等符号的上标表示样本索引号，下标表示样本向量的元素。对应模型结构图为

可以看到，通过张量形式表达网络结构，更加简洁清晰，同时也可充分利用张量计算的并行加速能力。那么怎么将图片识别任务的输入和输出转变为满足格式要求的张量形式呢?

考虑输入格式，一张图片使用矩阵方式存储，shape 为：[ℎ, ]，张图片使用 shape为[, ℎ, ]的张量 X 存储。而我们模型只能接受向量形式的输入特征向量，因此需要将[ℎ, ]的矩阵形式图片特征平铺成[ℎ ∗ ]长度的向量，如图 3.5 所示，其中输入特征的长度$d_{in}$ = ℎ ∗ 。

对于输出标签，前面我们已经介绍了数字编码，它可以用一个数字来表示便签信息，例如数字 1 表示猫，数字 3 表示鱼等。但是数字编码一个最大的问题是，数字之间存在天然的大小关系，比如1 < 2 < 3，如果 1、2、3 分别对应的标签是猫、狗、鱼，他们之间并没有大小关系，所以采用数字编码的时候会迫使模型去学习到这种不必要的约束。

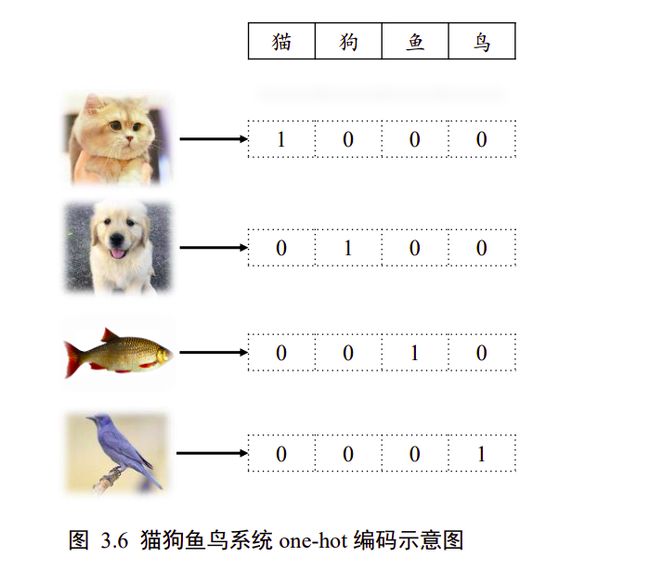
那么怎么解决这个问题呢？可以将输出设置为$d_{out}$个输出节点的向量，$d_{out}$与类别数相同，让第 ∈ [1, $d_{out}$]个输出值表示当前样本属于类别的概率(属于类别|)。我们只考虑输入图片只输入一个类别的情况，此时输入图片的真实的标注已经明确：如果物体属于第类的话，那么索引为的位置上设置为 1，其他位置设置为 0，我们把这种编码方式叫做 one-hot 编码(独热编码)。

以图 3.6 中的“猫狗鱼鸟”识别系统为例，所有的样本只属于“猫狗鱼鸟”4 个类别中其一，我们将第1,2,3,4号索引位置分别表示猫狗鱼鸟的类别，对于所有猫的图片，它的数字编码为 0，One-hot 编码为[1,0,0,0]；对于所有狗的图片，它的数字编码为 1，One-hot 编码为[0,1,0,0]，以此类推。

手写数字图片的总类别数有 10 种，即输出节点数$d_{out}$ = 10，那么对于某个样本，假设它属于类别，即图片的中数字为，只需要一个长度为 10 的向量，向量的索引号为的元素设置为 1，其他位为 0。

比如图片 0 的 One-hot 编码为[1,0,0,… ,0]，图片 2 的 Onehot 编码为[0,0,1,… ,0]，图片 9 的One-hot 编码为[0,0,0, … ,1]。One-hot 编码是非常稀疏(Sparse)的，相对于数字编码来说，占用较多的存储空间，所以一般在存储时还是采用数字编码，在计算时，根据需要来把数字编码转换成 One-hot 编码，通过 tf.one_hot即可实现

y=tf.constant([0,1,2,3])#数字编码
y=tf.one_hot(y,depth=10)#one-hot编码
print(y)

tf.Tensor(
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]], shape=(4, 10), dtype=float32)

现在我们回到手写数字图片识别任务，输入是一张打平后的图片向量 ∈ R${}^{28\ast 28}$，输出
是一个长度为 10 的向量 ∈ $R^{10}$，图片的真实标签 y 经过 one-hot 编码后变成长度为 10 的非 0 即 1 的稀疏向量$y\in \{0,1{\}}^{10}$。预测模型采用多输入、多输出的线性模型 $o=W^{\mathrm{T}}x+b$，其中模型的输出记为输入的预测值$o$ ，我们希望$o$越接近真实标签越好。我们一般把输入经过一次(线性)变换叫做一层网络。

3.3 误差计算

对于分类问题来说，我们的目标是最大化某个性能指标，比如准确度 acc，但是把准确度当做损失函数去优化时，会发现$\frac{\partial acc}{\partial \theta }$是不可导的，无法利用梯度下降算法优化网络参数。

一般的做法是，设立一个平滑可导的代理目标函数，比如优化模型的输出 与 Onehot 编码后的真实标签之间的距离(Distance)，通过优化代理目标函数得到的模型，一般在测试性能上也能有良好的表现。

因此，相对回归问题而言，分类问题的优化目标函数和评价目标函数是不一致的。模型的训练目标是通过优化损失函数ℒ来找到最优数值解$w^{\ast },b^{\ast }$:
$${\mathrm{W}}^{\ast },{\mathbf{b}}^{\ast }=\underset{W,\mathbf{b}}{\mathrm{argmin}}\mathcal{L}(\mathbf{o},\mathbf{y})$$
对于分类问题的误差计算来说，更常见的是采用交叉熵(Cross entropy)损失函数，而不是采用回归问题中介绍的均方差损失函数。我们将在后续章节介绍交叉熵损失函数，这里还是采用 MSE 损失函数来求解手写数字识别问题。对于个样本的均方差损失函数可以表达为：
$$\mathcal{L}(\mathbf{o},\mathbf{y})=\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^{10}{\left(o_j^i-y_j^i\right)}^2$$
现在我们只需要采用梯度下降算法来优化损失函数得到W, 的最优解，利用求得的模型去预测未知的手写数字图片 ∈ 。

3.4 真的解决了吗

按照上面的方案，手写数字图片识别问题真的得到了完美的解决吗？目前来看，至少存在两大问题：

❑ 线性模型 线性模型是机器学习中间最简单的数学模型之一，参数量少，计算简单，但是只能表达线性关系。即使是简单如数字图片识别任务，它也是属于图片识别的范畴，人类目前对于复杂大脑的感知和决策的研究尚处于初步探索阶段，如果只使用一个简单的线性模型去逼近复杂的人脑图片识别模型，很显然不能胜任

❑ 表达能力 上面的解决方案只使用了少量神经元组成的一层网络模型，相对于人脑中千亿级别的神经元互联结构，它的表达能力明显偏弱，其中表达能力体现为逼近复杂分布的能力

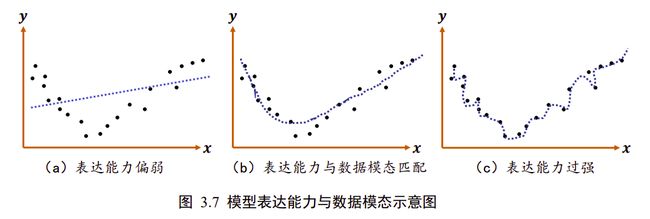
模型的表达能力与数据模态之间的示意图如图 3.7 所示，图中绘制了带观测误差的采样点的分布，人为推测数据的真实分布可能是某 2 次抛物线模型。

如图 3.7(a)所示，如果使用表达能力偏弱的线性模型去学习，很难学习到比较好的模型；如果使用合适的多项式函数模型去学习，则能学到比较合适的模型，如图 3.7(b)；但模型过于复杂，表达能力过强时，则很有可能会过拟合，伤害模型的泛化能力，如图 3.7©。

目前我们所采用的多神经元模型仍是线性模型，表达能力偏弱，接下来我们尝试解决这 2个问题。

3.5 非线性模型

既然线性模型不可行，我们可以给线性模型嵌套一个非线性函数，即可将其转换为非线性模型。我们把这个非线性函数称为激活函数(Activation function)，用表示：
$$\mathbf{o}=\sigma (\mathbf{W}\mathbf{x}+\mathbf{b})$$
这里的代表了某个具体的非线性激活函数，比如 Sigmoid 函数(图 3.8(a))，ReLU 函数(图3.8(b))。

ReLU 函数非常简单，仅仅是在 = 在基础上面截去了 < 0的部分，可以直观地理解为 ReLU 函数仅仅保留正的输入部分，清零负的输入。虽然简单，ReLU 函数却有优良的非线性特性，而且梯度计算简单，训练稳定，是深度学习模型使用最广泛的激活函数之一。我们这里通过嵌套 ReLU 函数将模型转换为非线性模型：
$$\mathbf{o}=\mathrm{ReLU}(\mathbf{W}\mathbf{x}+\mathbf{b})$$

3.6 表达能力

针对于模型的表达能力偏弱的问题，可以通过重复堆叠多次变换来增加其表达能力：
$${\mathbf{h}}_1=\mathrm{ReLU}\left({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1\right)$$
$${\mathbf{h}}_2=\mathrm{ReLU}\left({\mathbf{W}}_2{\mathbf{h}}_1+{\mathbf{b}}_2\right)$$
$$\mathbf{o}={\mathbf{W}}_3{\mathbf{h}}_2+{\mathbf{b}}_3$$

把第一层神经元的输出值作为第二层神经元模型的输入，把第二层神经元的输出作为第三层神经元的输入，最后一层神经元的输出作为模型的输出 。

从网络结构上看，如图 3.9 所示，函数的嵌套表现为网络层的前后相连，每堆叠一个(非)线性环节，网络层数增加一层。

我们把数据节点所在的层叫做输入层，每一个非线性模块的输出连同它的网络层参数和称为一层网络层，特别地，对于网络中间的层，叫做隐藏层，最后一层叫做输出层。这种由大量神经元模型连接形成的网络结构称为(前馈)神经网络(Neural Network)。

现在我们的网络模型已经升级为为 3 层的神经网络，具有较好的非线性表达能力，接下来我们讨论怎么优化网络。

3.7 优化方法

对于仅一层的网络模型，如线性回归的模型，我们可以直接推导出$\frac{\partial L}{\partial w}$和$\frac{\partial L}{\partial b}$的表达式，然后直接计算每一步的梯度，根据梯度更新法则循环更新, 参数即可。

但是，当网络层数增加、数据特征长度增大、添加复杂的非线性函数之后，模型的表达式将变得非常复杂，很难手动推导出梯度的计算公式；而且一旦网络结构发生变动，网络的函数模型也随之发生改变，依赖人工去计算梯度的方式显然不可行。

这个时候就是深度学习框架发明的意义所在，借助于自动求导(Autograd)技术，深度学习框架在计算函数的损失函数的过程中，会记录模型的计算图模型，并自动完成任意参数的偏导分$\frac{\partial L}{\partial \theta }$的计算，用户只需要搭建出网络结构，梯度将自动完成计算和更新，使用起来非常便捷高效。

3.8 手写数字图片识别体验

本节我们将在未介绍 TensorFlow 的情况下，先带大家体验一下神经网络的乐趣。本节的主要目的并不是教会每个细节，而是让读者对神经网络算法有全面、直观的感受，为接下来介绍 TensorFlow 基础和深度学习理论打下基础。让我们开始体验神奇的图片识别算法吧！

网络搭建 对于第一层模型来说，他接受的输入 ∈ $R^{784}$，输出 ∈ $R^{256}$设计为长度为 256的向量，我们不需要显式地编写${\mathbf{h}}_1=\mathrm{ReLU}\left({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1\right)$的计算逻辑，在 TensorFlow 中通过一行代码即可实现：

layers.Dense(256, activation='relu')

使用 TensorFlow 的 Sequential 容器可以非常方便地搭建多层的网络。对于 3 层网络，我们可以通过

keras.sequential([
    layers.Dense(256,activation='relu'),
    layers.Dense(128,activation='relu'),
    layers.Dense(10)])

快速完成 3 层网络的搭建，第 1 层的输出节点数设计为 256，第 2 层设计为 128，输出层节点数设计为 10。直接调用这个模型对象 model(x)就可以返回模型最后一层的输出 。

模型训练 得到模型输出$\mathbf{o}$后，通过 MSE 损失函数计算当前的误差ℒ：

with tf.GradientTape() as tape:#构建梯度记录环境
    #打平，[b,28,28] =>[b,784]
    x=tf.reshape(x,(-1,28*28))
    #step1. 得到模型输出 output
    # [b,784] =>[b,10]
    out=model(x)

再利用 TensorFlow 提供的自动求导函数 tape.gradient(loss, model.trainable_variables)求出模型中所有的梯度信息$\frac{\partial L}{\partial \theta }$ , ∈ {1, ,2, ,3, }：

# Step3. 计算参数的梯度 w1, w2, w3, b1, b2, b3
 grads = tape.gradient(loss, model.trainable_variables)

计算获得的梯度结果使用 grads 变量保存。再使用 optimizers 对象自动按着梯度更新法则
$${\theta }^{\prime }=\theta -\eta \ast \frac{\partial \mathcal{L}}{\partial \theta }$$
去更新模型的参数。

grads = tape.gradient(loss, model.trainable_variables)
 # w' = w - lr * grad，更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))

循环迭代多次后，就可以利用学好的模型去预测未知的图片的类别概率分布。模型的测试部分暂不讨论。

手写数字图片 MNIST 数据集的训练误差曲线如图 3.10 所示，由于 3 层的神经网络表达能力较强，手写数字图片识别任务简单，误差值可以较快速、稳定地下降，其中对数据集的所有图片迭代一遍叫做一个 Epoch，我们可以在间隔数个 Epoch 后测试模型的准确率等指标，方便监控模型的训练效果。

3.9 小结

本章我们通过将一层的线性回归模型类推到分类问题，提出了表达能力更强的三层非线性神经网络，去解决手写数字图片识别的问题。本章的内容以感受为主，学习完大家其实已经了解了(浅层)的神经网络算法，接下来我们将学习 TensorFlow 的一些基础知识，为后续正式学习、实现深度学习算法打下夯实的基石。

参考文献

• https://towardsdatascience.com/how-to-teach-a-computer-to-see-with-convolutional-neural-networks-96c120827cd1
• Y. Lecun, L. Bottou, Y. Bengio 和 P. Haffner, “Gradient-based learning applied to
  document recognition,” 出处 Proceedings of the IEEE, 1998.