北邮工程计算-知识点索引--十安辰
第二讲
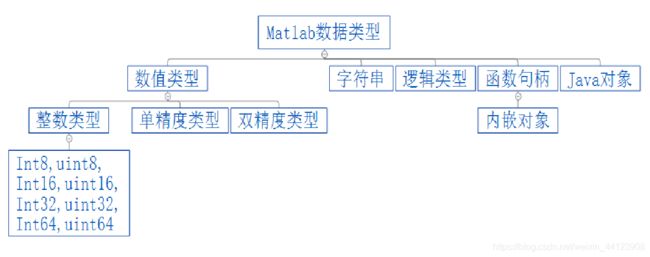
1、数据类型
整数、
浮点数与精度函数realmin、realmax 、eps、
intmax和intmin
字符型
逻辑型
complex()
复数的虚部和实部imag()、real()
复数的模、辐角和共轭复数abs()、angle ()、conj ()
2、数据结构
矩阵 、多维数组
字符串与字符串矩阵
单元数组 (cell array):cell(m, n)、按单元索引法、按内容索引法、celldisp()函数、 cellplot(b)、删除 、内容获取变维处理 reshape()
结构体 :struct()、查询、删除、调用成员变量
3、基本运算
关系运算 :小于(<)、小于或等于(< =)、大于(>)、大于或等于(> =)、等于(= =)和不等于(~ =)
逻辑运算:&、&&、|、|| 和~、逻辑“异或”,即“XOR
关系与逻辑函数 :
标点符号的使用
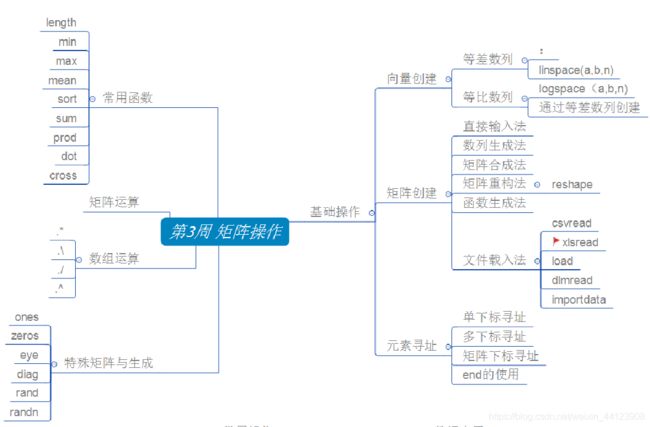
第三讲 向量、数组和矩阵
1 向量、数组与矩阵的创建
a=i:k:j、linspace()函数、logspace(a,b,n)
转置、点转置、适用于向量的常用函数
直接输入法、数列生成法、矩阵合成法、矩阵重构法、函数生成法(zeros,ones, eye,rand,randn,diag,triu,tril)、文件载入法(load, xlsread, csvread, …)
2 向量、数组和矩阵的寻址与赋值
下标索引 、双下标、冒号表达式选择行、列或数组元素、end关键字
矩阵元素的删除
创建任意数q为底的等比数列:
a=ones(n,1);
a(2:end)=q;
b=cumprod(a);
3 标准矩阵与特殊矩阵
全1矩阵 ones()、全0矩阵zeros()、随机矩阵 rand()、 randn()
随机整数序列的生成
单位矩阵eye()、对角矩阵diag(v,k)
4 基本的四则运算
向量与数的加法(减法)、乘法(除法)
矩阵的乘法、除法
5 向量、数组和矩阵的其他运算
向量、数组的乘方运算:power()函数c = a.^k= c = power(a,k)
矩阵的乘方与mpower()函数
求极小值与极大值
求和sum()、求积prod()、
第四讲 MATLAB程序设计
1 程序结构
顺序结构、分支结构和循环结构
2 循环程序
for循环:for variable = values commands end
键盘输入函数为input()
while 循环:
while expression
commands
end
break语句、 continue语句
3 分支结构
if…end、if…else…end、if…elseif…else…end
switch开关结构
switch expression
case expression_1
commands_1
case expression_2
commands_2
...
otherwise
commands
end
第五讲 M脚本与M函数
1 使用M文件编程
2 M函数
function f = fact(n)
#函数定义语句
% Compute a factorial value. H1行
% FACT(N) returns the factorial of N, 帮助文本
% usually denoted by N!
% Put simply, FACT(N) is PROD(1:N). 注释语句
f = prod(1:n); %函数体
块注释 :“%{”和“%}”符号进行块注释
代码元胞 :“%%”为开始标志
M文件的命名规则
局部变量
全局变量:global 变量名1 变量名2
永久变量:persistent 变量名1 变量名2
3 函数的调用与函数句柄
匿名函数:fhandle = @(arglist) expr
获取函数的输入、输出参量数目:nargin()和nargout()
4 函数编程的实例
第六讲 图形绘制
5.1 绘制二维图
绘制二维线性图plot()
stem()绘制离散图形
对数图loglog()、semilogx()、semilogy()
polar()绘制极坐标图
5.2 常用图形的绘制
绘制直线line()函数
绘制矩形rectangle()函数
绘制偏差条图形errorbar()函数
绘制直方图与其正态分布曲线:hist()函数、rose()函数极坐标系中绘制直方图
填充图与面积图:fill()函数、area()函数
5.3 三维图形绘制
plot3()函数绘制三维曲线
mesh():mesh()函数可以绘制出在某一区间内完整的网格曲面
surf()函数:surf()函数可以绘制三维曲面图
meshgrid()函数:为3D绘图生成X、Y矩阵
meshc()和meshz()函数:meshc()与mesh()函数的调用方式相同,只是该函数在mesh()的基础上又增加了绘制相应等高线的功能。
彗星图:comet()、comet3()可用来绘制2D和3D彗星图
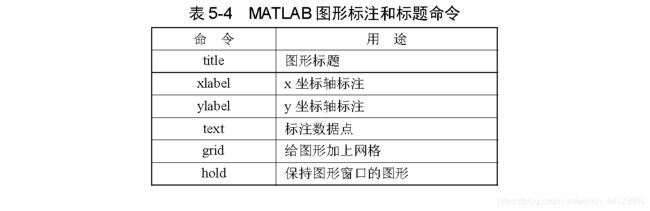
5.4 绘图控制
图形窗口的创建:figure
指定图像位置和大小
图形保持与多重线绘制: hold on,plot(x1,y1,x2,y2,…,xn,yn)
子图控制与subplot()函数:subplot(m,n,p)
使用legend命令或函数添加图例
坐标轴的控制函数axis()、xlim()、ylim()、zlim()函数
5.5 特殊图形的绘制
绘制二维柱状图:bar()和barh()
绘制三维柱状图:bar3()和bar3h()
绘制阶梯图形:stairs()
方向和速度矢量图形 :compass()
罗盘图的绘制 :compass()
羽状图的绘制 :feather()
矢量图的绘制:quiver()和quiver3()
饼形图:pie()函数和pie3()函数
第七讲-1特殊图形的绘制
1 柱状图绘制
2 结题图形绘制
3 方向和速度矢量图
4 等值线绘制
5 三位旋转图形绘制
第七讲-2误差理论
1 误差的来源
模型误差 、观测误差、截断误差、舍入误差
2 误差表示法
3 误差的积累与传播
4 工程计算中应注意的问题
5 MATLAB数据精度控制
第八讲 符 号 运 算
8.1 符号对象
符号变量、符号矩阵、符号表达式和符号方程
sym()和syms()函数建立符号表达式
8.2 数值与符号变量的相互转换
digits():digits(n):设置有效数字位数
vpa():vpa(f)将符号表达式f的结果精确到digits()所设定的有效数字的位数
double():double()是将符号表达式转换为浮点数数值变量类型的函数
**poly2sym()**函数与多项式的符号表达式
8.3 符号矩阵与运算
符号矩阵的索引和修改:
符号矩阵的索引:
符号矩阵的修改
8.4 符号表达式的化简
合并多项式:collect()
展开多项式:expand()
转换多项式:horner()
化简函数:simplify()
因式分解:factor()
分式通分:[B.A]=numden(F)、
符号替换:subs() 函数、subexpr() 函数
8.5 符号微积分
符号表达式求极限:limit()函数
符号导数、微分和偏微分:diff()函数
多元函数的导数与 jacobian() 函数
计算不定积分、定积分:int()函数
8.6 符号方程与求解
解代数方程:solve()
代数方程组的符号解法:solve()函数
常微分方程的解析解:使用dsolve()函数进行求解
微分方程组的求解:dsolve()函数
8.7 符号函数图形绘制
符号函数二维绘图函数 :fplot()
符号函数三维绘图函数 :fplot3()
符号函数曲面网格图及表面图的绘制:fmesh()、fsurf() 函数
第九讲 非线性方程(组)求解
9.1 二分法
9.2 简单迭代法
9.3 牛顿法
9.4 非线性方程组的求解
MATLAB优化工具箱提供了两个函数: fzero() 和 fsolve() 函数,分别用来求解非线性方程和非线性方程组的根。
1、fzero() 函数
作用:求解单变量非线性方程的根。
调用格式: [x, fval, exitflag, output] = fzero(fun,x0,options, p1,p2,…)
2、fsolve()作用:求解多变量非线性方程组的根。
调用格式: [x,fval, exitflag, output, jacobian] = fsolve(fun,x0,options, p1,p2,…)
第十讲 线性方程(组)求解
10.1 消去法
10.1.1 GAUSS 消去法
10.1.2 追赶法
10.2 矩阵分解法
10.2.1 LU 分解
MATLAB 提供了矩阵的 LU 分解函数 lu(),该函数的调用格式为
[L,U]=lu(A) %格式 1
[L,U,P]=lu(A) %格式 2
其中格式 1 的输入参数与输出参数的关系满足关系式 其中 为单位下三角阵, 为单位上三
角阵;
格式 2 中的 为单位矩阵的行变换矩阵(因为 MATLAB 提供的 lu()函数使用了部分选主元算法),这
里的输入参数和输出参数满足关系 L U = P A LU=PA LU=PA
10.2.2 Cholesky 分解
10.3 方程组的性态与误差分析
10.3.1 范数
MATLAB 提供了函数 **norm()**来求向量的范数,该函数的调用格式为:
norm(x,p)其中 x 为向量,p 为范数的类型,可以为任意实数或者 inf,表示求取向量 x 的 p-范数。
MATLAB 提供的求解矩阵范数仍是 norm()函数,不同在与 p 的取值限定为 1,2 和 inf, ‘fro’
10.3.2 矩阵的条件数
10.3.3 病态方程组的求解
MATLAB 中提供的实现矩阵的奇异值分解的函数时 svd(),该函数的调用格式为:
[U,S,V]=svd(A)
10.4 线性方程组的 MATLAB 函数求解
( 1 )恰定方程组
MATLAB 主要提供的求解指令主要有三个
1)逆矩阵法:x=inv(A)*b(或 x=A^(-1)*b)
- 伪逆法:x=pinv(A)*b
3)左除法:x=A\b 4) 符号矩阵:x=sym(A)\sym(b)
说明:
1)通常情况下,利用逆矩阵法和左除法求得的均是数值解,若要得到其解析解,则要将数值矩阵转化
为符号矩阵
2)左除法比逆矩阵法具有更好的数值稳定性,更快的运算速度,而且左除法还适合 不是方阵的情形
( 2 )欠定方程组
欠定方程组 的解由其对应的齐次方程 的通解和它本身的一个特解构成,记作
。MATLAB 求方程 通解的指令是 null(),其具体的使用方法为
z=null(sym(A)),该函数也同样可以用于数值解的问题,其中 z 的列数为 n-rank**(****A)**,其各列构成的
向量称为矩阵 的基础解系。求方程 的一个特解只需要左除法即可。
( 3 )超定(矛盾)方程组
因为超定方程组一般意义下无解析解,所以不能用符号矩阵出发来求解方程组,而只能求其最小二乘
解,这也可以通过左除法或伪逆法来实现。
function [x,e]=Linear_equation(A,b)
% 线性方程组的求解
% 输入参数:
% ‐‐‐A:方程组的系数矩阵
% ‐‐‐b:方程组的右端向量
% 输出参数:
% ‐‐‐x:方程组的解
% ‐‐‐e:解的误差
[m,n]=size(A);
r1=rank(A);
r2=rank([A b]);
if r1==r2
if r1==n
disp('方程组是恰定的,有唯一解!')
x=A\b;
e=norm(A*x‐b);
else
disp('方程组是欠定的,有无穷解!')
z=null(sym(A)); %解出规范化的化零空间
x0=sym(A)\sym(b); %求出一个特解
colnum = size(z,2);
k =[];
for i = 1:colnum
k = [k sym(['k' num2str(i)])];
end
x = z*k+x0;
e=norm(A*x‐b); %检验解的准确性
end
else
disp('方程组是超定的,只有最小二乘意义下的解!')
x=A\b;
e=norm(A*x‐b);
end
第十一讲 插 值
11.1 插值概述
11.2 Lagrange插值
11.3 Newton插值
11.4 Hermite插值
11.5 分段低次插值
11.5.1 分段线性插值
MATLAB提供了函数interp1()可以实现分段线性插值功能,调用方法如下:
y=interp1(x,y,xi,'linear')
11.5.2 分段插值
MATLAB提供了函数**pchip()**来求解分段三次Hermite插值,该函数的调用格式有以下两种:
yi=pchip(x,y,xi)%格式一
pp=pchip(x,y)%格式二
其中,输入参数的含义同interp1()函数,格式2中的返回值pp是一个结构体数组,需要调用ppval()函数来计算各因
变量的数值。
说明:
(1)语句“yi=ppval(pp,xi)"可以实现与格式一相同的功能;
(2)函数pchip()的效果等同于yi=interp1(x,y,xi,‘pchip’)或yi=interp1(x,y,xi,‘cubic’)。
11.6 三次样条插值
MATLAB提供函数spline()求解三次样条插值问题,该函数的一般调用格式有两种:
yi=spline(x,y,xi)%格式一
pp=spline(x,y)%格式二
其中各参数的含义同函数pchip()
说明:
(1)语句“yi=ppval(pp,xi)"可以实现与格式一相同的功能;
(2)函数spline()的 效果等同于yi=interp1(x,y,xi,‘spline’)。
11.7 二维插值
11.7.1 网格节点插值
对于网格节点的插值,MATLAB提供了函数**interp2()**求解,其具体调用格式如下:
zi=interp2(x,y,z,xi,yi,method)%格式一
zi=interp2(x,y,z,xi,yi,method,extrapval)%格式二
其中,x和y是长度分别为M和N的向量,对应着已知点 ( x i , y i ) (x_i,y_i) (xi,yi) ,z是一个矩阵,对应
于 Z i , j ( i = 0 , 1 , 2 , 3... , n ) Z_{i,j}(i=0,1,2,3...,n) Zi,j(i=0,1,2,3...,n),其他参数的含义基本同interp1()函数。
11.7.2 散乱节点插值
MATLAB提供函数**griddate()**来求解散乱节点插值问题,该函数的调用格式为:
zi=griddata(x,y,z,xi,yi,method)
其中,x,y和z是给定的节点数据,xi和yi通常是规则的网格点,method表示可供选择的插值法,包括以下几种:
⋅’linear‘—基于三角形的线性插值(默认值)
⋅’cubic’—基于三角形的三次插值;
⋅‘nearest’—最邻近插值;
⋅’v4’—MATLAB中的griddata算法。
第十二讲 函数逼近与数据拟合
12.1 函数的最佳平方逼近
12.2 数据的最小二乘拟合
12.2.1 最小二乘法
12.2.2 多元最小二乘拟合
12.2.3 数据拟合的MATLAB函数求解
**1.**线性拟合
MATLAB最优化工具箱提供了函数 lsqlin() 求解上述问题,下面用一个实例说明该函数的使用方法。
2. 多项式拟合
在最小二乘拟合中,当拟合基函数选取幂函数类 时,相应的拟合称为多项式拟合。
MATLAB提供的 polyfit() 函数是专门用来求解多项式拟合的函数,其调用格式为:
[p,S]=polyfit(x,y,n) %格式1
[p,S,mu]=polyfit(x,y,n) %格式2
其中格式1是一般的多项式拟合,格式2是对x归一化处理后的多项式拟合,等价格式为:
[p,S]=polyfit((x-mean(x))/std(x),y,n)
x,y是输入的实验数据;mean(x)返回向量x的平均值,std(x)返回向量x的标准差,n是拟合计算用到的多项式的阶数;返回值p是拟合多项式系数;S是用来估计误差和预测数据的结构体;mu是由均值和标准差构成的1x2向量,即mu=[mean(x),std(x)]。
与 polyfit() 函数配合使用的函数是 polyval(),这个函数是根据拟合出来的多项式系数p计算给定数据x处的y值。
其调用格式如下:
[Y,DELTA]=polyval(p,X,S)
[Y,DELTA]=polyval(p,X,S,mu)
其中X是给定的需要计算拟合值的向量;p,S,mu是polyfit()函数的返回值;返回值Y是根据p计算出来的X处的多
项式的值;DELTA是利用结构体S计算出来的误差估计,Y的95%置信区间为[Y-DELTA,Y+DELTA],当DELATA
缺省时,S可以为’[]’
3. 非线性拟合
在最小二乘拟合中,若要寻求的函数**f(x)**是任意的非线性函数,则称为非线性最小二乘拟合,由该定义可知多项
式拟合是一种特殊的非线性拟合。
MATLAB最优化工具箱中提供了 lsqcurvefit() 函数,可以解决非线性最小二乘拟合问题,该函数的调用格式为:
[x,resnorm,residual,exitflag,output,lambda,jacobian]=lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options,p1,p2,...)
其中,fun是非线性函数模型;x0是最优化的初始值;xdata,ydata是原始输入输出数据向量;返回值x为拟合输出
的未知参数,其他参数的含义可查询帮助文档。
**4.**多元非线性拟合
MATLAB统计工具箱中提供的求解多元非线性回归的函数nlinfit()可以满足要求,该函数的调用格式为;
[bata,r,J]=nlinfit(X,y,fun,beta0,options)
其中beta是返回的回归系数,这里也就是拟合系数,r是残差,J是Jacobian矩阵;输入数据x、y分别为mn矩阵
和n维列向量,对一元非线性回归x为n维列向量;fun是回归模型的数学表达式,beta0是预先设定的回归系数初
值,options是控制参数选项,它可以通过statset()函数来设置,至于相关的属性及属性名可参阅帮助文档。
第十三讲 数值积分
8.1 插值型求积方法
8.2 自适应步长求积方法
8.3 Gauss求积方法
8.4 特殊函数的积分
8.5 数值积分的MATLAB函数求解
8.5.1 trapz()函数
MATLAB中的trapz()函数是基于复化梯形公式设计编写的,其一般调用格式为:
I=trpaz(x,y,dim)
其中x,y是观测数据,x可以为行向量或列向量,y可以为向量或矩阵,y的行数应等于x向量的元素个数;
dim表示按维进行求积,若dim=1(默认值),则按行求积,若dm=2,则按列求积。
8.5.2 quad()函数
MATLAB提供的quad()函数也是基于自适应辛普森法设计的,该函数的调用格式为:
[q,fcnt] =quad(fun,a,b,tol,trace,p1,p2,…)
其中fun是被积函数,可以是字符表达式、内联函数、匿名函数和M函数;a,b是定积分的上限和下限;
tol为指定的误差限,默认值为;trace提供中间输出[fcnt ab-aq],若trace=[],则quad不提供中间输出;
pl,p2…是函数fun的附加参数。
q是返回的数值积分;fcnt是返回函数评估的次数
另外,MATLAB还提供了一个新的函数quadl(),其调用格式与quad()函数完全一致,使用的算法是自适应Lobatto算法,其精度和速度均远高于quad()函数,所以在追求高精度数值解时建议使用该函数。
8.5.3 quadgk()函数
quadgk()函数是MATLAB R2007b版本提供的基于Gauss-Kronrod算法实现的数值积分数,该函数可以用来求解振荡函数的积分、广义积分甚至是复数积分,其一般调用格式为:[q,errbnd]=quadgk(fun,a,b,param1,val1,param2,val2,…)
其中fun是被积函数,可以是字符表达式、内联函数、匿名函数和M函数;
a,b是积分的上限和下限,它们可以为-inf和inf;parami,vali是指相关属性名及其属性值。
8.5.4 dblquad()函数
对于长方形区域的双重积分,可以由MATLAB提供的dblquad()函数得出,该函数的调用格式为:
q=dblquad(fun,xmin,xmax,ymin,ymax,tol,@quadl,pl,p2,…),
其中,输入参数@quadl为具体求解一元积分的数值函数,也可以选择@quad甚至用户自己编写的数值积分求解函数,但要求其调用格式与quadl()函数完全一致,其余参数大致同函数quadl()。
文章仅供参考,请勿照搬照抄!转载请说明出处!
CSDN–十安辰 --链接:https://blog.csdn.net/weixin_44123908