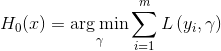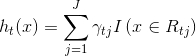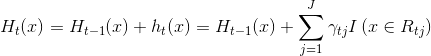【机器学习】深入剖析梯度提升决策树(GBDT)分类与回归
1. 梯度提升决策树概述
梯度提升决策树(Gradient Boosting Decision Tree,GBDT)是以决策树为基学习器的一种Boosting算法,它在每一轮迭代中建立一个决策树,使当前模型的残差在梯度方向上减少;然后将该决策树与当前模型进行线性组合得到新模型;不断重复,直到决策树数目达到指定的值,得到最终的强学习器。
上一篇博客【机器学习】集成学习——Boosting与AdaBoost原理详解与公式推导对AdaBoost算法做了总结,GBDT与AdaBoost的主要区别有:
1. 迭代策略不同:AdaBoost在每一轮迭代中都要更新样本分布;GBDT迭代学习上一轮得到的加法模型与真实值之间的残差,它并不显式改变样本分布,而是利用残差变相地增大错误样本的权重。
2. 组合策略不同:AdaBoost中误差率越低的基学习器在最终模型中所占比重越高,而GBDT每棵树的权值都相等。
3. 基学习器限定不同:AdaBoost的基学习器不限,使用最广泛的是决策树和神经网络;而GBDT的基学习器限定为决策树,且是回归树。
4. 损失函数不同:AdaBoost分类算法的损失函数限定为指数损失,而GBDT可以是指数损失函数和对数似然函数。
2. 提升树
在介绍梯度提升决策树之前,我们首先来介绍提升树。
介绍了提升方法本身是采用加法模型和前向分步算法的一种方法,而提升树(Boosting Tree)是以决策树为基学习器的一种提升方法,对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
提升树模型可以表示为决策树的加法模型:
其中,![]() 表示第
表示第![]() 棵决策树;
棵决策树;![]() 是的参数;
是的参数;![]() 是决策树个数。
是决策树个数。
根据前向分步算法,第![]() 步将要得到的提升树模型为:
步将要得到的提升树模型为:
![]() (2)
(2)
其中,![]() 为当前模型。那么第
为当前模型。那么第![]() 轮迭代的目标是得到能最小化
轮迭代的目标是得到能最小化![]() 的损失函数的第
的损失函数的第![]() 棵决策树
棵决策树![]() 的参数,即:
的参数,即:
对于二类分类问题,只要把AdaBoost中的基分类器限定为二类分类树即可。可以说这时的提升树是AdaBoost的特殊情况。
对于回归问题,当采用平方误差损失函数![]() 时,第
时,第![]() 次迭代的损失是:
次迭代的损失是:
当![]() 时,损失最小。也就是说,第
时,损失最小。也就是说,第![]() 次迭代的优化目标是拟合当前模型的残差。
次迭代的优化目标是拟合当前模型的残差。
3. 梯度提升决策树原理
在提升方法中,每次迭代的优化问题可以分为两部分:一、求叶结点区域;二、给定叶结点区域,求区域内最优拟合值。
对于第二个问题,它是一个简单的“定位”估计,最优解很容易得到;但对于第一个问题,当损失函数不是平方误差和指数损失,而是一般损失函数时,求解区域是困难的,最小化损失函数问题的简单、快速求解算法是不存在的。
针对这一问题,梯度提升决策树利用最速下降法来近似求解加法模型中的每一颗决策树,具体来说,就是在每次迭代中,使新建的决策树都沿损失函数减少最快的方向——负梯度方向减少损失函数。
当前模型的负梯度为:
当损失函数是平方误差时,当前模型的负梯度就等于残差,沿负梯度方向减少损失函数就相当于拟合残差。
但当损失函数不是平方误差时,负梯度就是残差的近似值,称为“广义残差或伪残差”。例如,当损失函数是绝对误差时,负梯度是残差的符号函数,因此在每次迭代时,决策树将拟合当前残差的符号。
总之,GBDT利用广义残差来拟合每一轮迭代中的回归树。
一些广泛应用的损失函数的梯度如下表:
4. GBDT回归算法
下面介绍GBDT回归算法,也可以当做GBDT的通用算法。必须声明的是,无论是GBDT分类算法还是回归算法,弱学习器都是回归树,这是由残差本质决定的。
输入:训练集![]() ,其中
,其中![]() ,
,![]() ;损失函数
;损失函数![]() 。
。
过程:
(1)初始化模型![]() ,估计使损失函数最小化的常数值
,估计使损失函数最小化的常数值![]() ,初始模型是只有一个根结点的树。
,初始模型是只有一个根结点的树。
(2)对迭代轮次![]()
(a)对样本![]() ,计算当前模型的广义残差:
,计算当前模型的广义残差:
(b)利用![]() 拟合一棵回归树,得到第
拟合一棵回归树,得到第![]() 棵树的叶结点区域
棵树的叶结点区域![]() ;
;
(c)对每个叶结点区域![]() ,计算能使区域
,计算能使区域![]() 损失函数最小化的最佳预测值
损失函数最小化的最佳预测值![]() :
:
(d)得到本轮迭代最佳拟合回归树:
(e)更新本轮迭代的加法模型:
(3)得到最终的强学习器:
输出:回归树![]() 。
。
5. 二元GBDT分类算法
在分类任务中,由于样本输出是离散值,无法从输出类别拟合残差,因此使用类别的预测概率值和真实概率值的差来当做残差。
GBDT分类算法的损失函数可以取指数损失函数和对数似然函数,如果选择指数损失函数,则GBDT退化为AdaBoost。因此我们这里只讨论对数似然损失函数。
二元分类的对数似然损失函数是:
![]() (6)
(6)
负梯度为:
利用![]() 拟合一棵回归树,得到第
拟合一棵回归树,得到第![]() 棵树的叶结点区域
棵树的叶结点区域![]() ;
;
每个叶结点区域![]() 的最佳预测值
的最佳预测值![]() 为:
为:
由于上式比较难优化,我们用近似值代替:
除了负梯度计算和叶子节点最佳预测值计算不同,其他都与回归算法一致。
6. GBDT优缺点
优点:
1. 可以灵活处理混合型数据(异构特征);
2. 强大的预测能力;
3. 在输出空间中对异常点的鲁棒性(通过具有鲁棒性的损失函数实现,如Huber损失函数和分位数损失函数)。
缺点:
1. 在更大规模的数据集或复杂度更高的模型上的可扩展性差;
2. 由于提升算法的有序性,因此很难做到并行。
参考文献:
1. 《统计学习方法》第八章提升方法——李航
2. 《统计学习基础》第十章提升和加法树——Trevor Hastie等
3. 论文《Greedy Function Approximation: A Gradient Boosting Machine》——Jerome H. Friedman
4. 梯度提升树(GBDT)原理小结
5. GBDT原理详解
6. Scikit-learn 0.19.x 中文文档 Gradient Tree Boosting(梯度树提升)
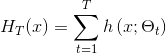
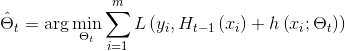
![\begin{array}{l} L\left( {y,{H_t}(x)} \right) = L\left( {y,{H_{t - 1}}(x) + h\left( {x;{\Theta _t}} \right)} \right)\\ {\rm{ = }}{\left[ {y - {H_{t - 1}}(x) - h\left( {x;{\Theta _t}} \right)} \right]^2}\\ {\rm{ = }}{\left[ {{r_t} - h\left( {x;{\Theta _t}} \right)} \right]^2} \end{array}](http://img.e-com-net.com/image/info8/60f0356a18954d2f8cf798d37b606bc3.gif)