控制教程 —— 介绍篇：2.系统分析

承接上一篇(控制教程 —— 介绍篇：1.建模)。
一旦获得了系统的状态空间或传递函数形式的数学模型，我们便可以分析这些模型来预测系统在时域和频域中的动态响应。通常将控制系统设计为高稳定性，高响应速度，低稳态误差，以及减小振荡。也就是“稳准快”。在本节中，我们将展示如何从系统模型中确定这些动态属性。
本教程中使用的主要MATLAB命令是：

时域响应概述

时域响应表示动态系统的状态在受到特定输入时随时间的变化。由于我们得出的模型由微分方程组成，因此必须执行一些积分以确定系统的时域响应，对于某些简单的系统，可以使用闭区间的形式分析解决。但是，对于大多数系统，尤其是非线性系统或需要复杂输入的系统，此积分必须以数字方式进行，幸运的是，MATLAB提供了许多有用的资源来计算多种类型的输入来获得时域响应。
线性动态系统的时域响应又瞬态响应和稳态响应组成，瞬态响应取决于初始条件，稳态响应取决于系统输入，这些分别对应于齐次微分方程的特定解。

频域响应概述

本教程中介绍的所有示例均通过线性常数系数微分方程建模，因此均为线性不变(LTI)。LTI系统具有极其重要的特性，如果系统的输入为正弦波，则稳态输出也将是相同频率的正弦波，但通常具有不同的幅度和相位。这些幅度和相位差表示为频率的函数，即组成了系统的频率响应。
可以通过以下方式从系统的传递函数中找到系统的频域响应：创建频率向量(从0到无穷大之间变化)，并计算在这些频率下的传递函数的值。如果 $G(s)$是系统的开环传递函数，而$\omega$是频率矢量，则可以绘制 $G(j\omega )$ 与 $\omega$的关系图。由于$G(j\omega )$是复数，因此我们可以绘制其幅值和相位(伯德图)，也可以绘制其在复平面上的位置(奈奎施特图)，两种方法显示相同的信息，但方式不同。

稳定性

出于我们的目的，我们将使用“有界输入有界输出”**(BIBO)**的稳定性定义，该定义指出如果输出对所有输入保持有界，则系统是稳定的。实际上，这意味着系统在运行时不会“发散”。
传递函数表示法在分析系统稳定性时特别有用，如果传递函数的所有极点(分母等于0的$s$的值)都为负实部，则系统是稳定的。如果任一极点具有正实部，则系统不稳定。如果我们查看复数s平面上的极点，则所有极点都必须在左半平面(LHP)中来确保稳定性。如果在虚轴上有任何一对对偶极点，则系统在一定程度上是稳定的，并且系统将趋于振荡，具有纯虚数极点的系统不被认为是BIBO稳定的，对于这样的系统，将存在无界响应的有界输入。LTI系统模型的极点可以使用pole，其示例如下所示：

s = tf('s');
G = 1/(s^2+2*s+5)
pole(G)

可以看出极点的实部均为负值，因此系统是稳定的。系统的稳定性也可以从状态空间表示中找到，实际上，传递函数的极点是系统矩阵$A$的特征值，我们可以使用eig命令，表达形式是eig(G)，来计算系统矩阵的特征值，如下所示：

[A,B,C,D] = ssdata(G);
eig(A)

系统的阶

动态系统的阶是其微分方程的最高导数的阶，同样，它是传递函数分母中$s$的最高次幂。一、二阶和高阶系统的重要特性将在下面进行回顾。

一阶系统

一阶系统是最简单的动态系统，一些常见的示例包括质量块阻尼系统和RC电路。
一阶微分方程的一般形式如下
$$\dot{y}+ay=bu\text{or}\tau \dot{y}+y=k_{dc}u$$，一阶传递函数的形式是：
$$G(s)=\frac{b}{s+a}=\frac{k_{dc}}{\tau s+1}$$其中参数$k_{dc}$ 和 $\tau$ 表征了一阶系统的行为
直流增益
直流增益$k_{dc}$是稳态阶跃响应的幅度与阶跃输入的幅度之比。对于稳定的传递函数，终值定理证明直流增益是在 $s$ = 0时的值。对于所示的一姐系统，直流增益为 $k_{dc}=b/a$。
时间常数
一阶系统的时间常数为 $T_c=\tau =1/a$，是系统对于阶跃输入的响应达到其稳态值的63%所需的时间(从零初始值开始)，或降低至系统响应初始值的37%，更一般而言，它代表了系统动态变化的时间尺度。
零极点
一阶系统只有一个极点，在这种情况下 $s=-a$，因此，如果$a$为正，则系统稳定；如果$a$为负，则系统不稳定，标准一阶系统没有零点。
阶跃响应
我们可以使用以下MATLAB命令计算对节约输入$u$的系统时间响应：

k_dc = 5;
Tc = 10;
u = 2;

s = tf('s');
G = k_dc/(Tc*s+1)

step(u*G)

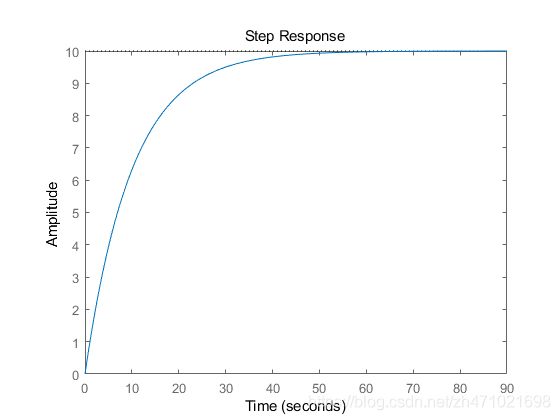
注意：MATLAB还提供了一个强大的图形用户界面来分析LTI系统，可以使用语法LinearSystemAnalyzer(‘step’,G)进行访问。
如果在阶跃响应图上单击鼠标右键，然后选择"Characteristics"，则可以选择在响应曲线上叠加几个系统指标，峰值响应，建立时间，上升时间和稳态值。

建立时间
建立时间$T_s$是系统输出与阶跃输入的稳态值之间的差下降到与在稳态值特定百分比(如2%)以内所需的时间，下表提供了最常见一阶系统的建立时间。可以看到差值越小，意味着建立时间越长

10%	5%	2%	1%
$Ts=2.3/a=2.3T_c$	$Ts=3/a=3T_c$	$Ts=3.9/a=3.9T_c$	$Ts=4.6/a=4.6T_c$

上升时间
上升时间$T_r$是系统输出从最终稳态的某个较低水平$x\%$上升至某个较高水平$y\%$所需的时间，对于一姐系统，典型范围是$10\%$ ~ $90\%$。
伯德图
伯德图显示了系统频率响应 $G(j\omega )$的大小和相位，相对于频率 $\omega$绘制。我们可以使用语法bode(G)在MATLAB中生成系统$G$的bode图，如下所示：

bode(G)

再次使用线性系统分析GUI，linearSystemAnalyzer(‘bode’,G)可以获得相同的结果。
伯德图采用对数频率标度，因此可以看到更大的频率范围。同样，使用对数分贝单位(dB)表示幅度，定义为：
$$M_{dB}=20{\log }_{10}(M)$$与频率轴一样，分贝标度使我们可以再单个图上查看更大范围的幅度。同样，正如我们将在后续教程中看到的那样，当模块与控制器串联放置时，整个系统的传递函数是各个传递函数的乘积，使用dB标度，整个系统的幅度图就是各个传递函数的幅度图的总和。整个系统的相位图也是各个相位图的总和。
一阶伯德图的低频幅度为$20\log (k_{dc})$，幅度图在等于极点绝对值的频率处有一个弯曲(即 $\omega =a$)，然后每增加10倍频率便会降低20dB(斜率=$-20$dB/十倍频)，在低频时，相位图渐进0度，而在高频时，渐进到$-90$度。在频率$0.1a$和$10a$之间，频率每增加十倍，相位变化约$-45$度($-45$/十倍频)。
在后续控制器设计的频率方法部分，我们将看到如何使用伯德图来计算闭环稳定性和反馈系统的性能。

二阶系统

二阶系统在实践中经常会遇到，并且是显示振荡的最简单的动态系统类型。例如包括质量块弹簧阻尼器系统和RLC电路，实际上，许多真实的高阶系统可以近似为二阶以便于分析。
二阶微分方程的规范形式如下
$$m\ddot{y}+b\dot{y}+ky=f(t)\text{or}\ddot{y}+2\zeta {\omega }_n\dot{y}+{\omega }_n^{2}y=k_{dc}{\omega }_n^{2}u$$规范的二阶函数具有以下形式，其中具有两个极点且没有零点。
$$G(s)=\frac{1}{m{s}^2+bs+k}=\frac{k_{dc}{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$参数 $k_{dc}$, $\zeta$, 和${\omega }_n$ 表征了典型二阶系统的行为。
直流增益
直流增益$k_{dc}$同样也是稳态阶跃响应的幅度与阶跃输入的幅度之比，对于稳定的系统，它是$s$=0时传递函数的值，对于给定的形式：
$$k_{dc}=\frac{1}{k}$$
阻尼比
阻尼比$\zeta$是一个无量纲的量，表征了系统响应的振动，由于诸如粘性摩擦或电阻之类的影响而衰减速率，根据以上定义：
$$\zeta =\frac{b}{2\sqrt{km}}$$
自然频率
自然频率 ${\omega }_n$ 是在没有阻尼的情况下($\zeta$=0)系统将振荡的频率(以rad/s为单位)：
$${\omega }_n=\sqrt{\frac{k}{m}}$$
零极点
规范的二阶传递函数有两个极点：
$$s_p=-\zeta {\omega }_n\pm j{\omega }_n\sqrt{1-{\zeta }^2}$$
欠阻尼系统
如果$\zeta <1$，则系统阻尼不足，在这种情况下，两个极点都具有负实数的复值，因此，系统是稳定的，但在接近稳态值时会震荡，具体而言，响应随着阻尼和自然频率而变化，即 ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$ (单位为rad/s)

k_dc = 1;
w_n = 10;
zeta = 0.2;

s = tf('s');
G1 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G1)
axis([-3 1 -15 15])

step(G1)
axis([0 3 0 2])

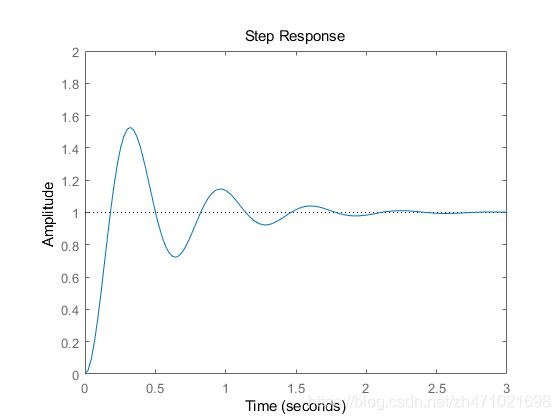
建立时间
建立时间 $T_s$ 是系统输出落入阶跃输入的稳态值的一定百分比内所需的时间，对于典型的二阶欠阻尼系统，建立时间可以通过以下公式估算：
$$T_s=\frac{-\ln (\mathrm{t}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n})}{\zeta {\omega }_n}$$下表列出了最常见范围的建立时间：

10%	5%	2%	1%
$T_s=2.3/(\zeta \ast w_n)$	$T_s=3/(\zeta \ast w_n)$	$T_s=3.9(\zeta \ast w_n)$	$T_s=4.6/(\zeta \ast w_n)$

超调
超调百分比是系统的阶跃响应超出最终稳态值得百分比，对于二阶欠阻尼系统，超调百分比 $Mp$ 通过以下公式与阻尼比直接相关，在此，$Mp$ 是一个十进制数，其中1对应于100%的超调。
$$Mp=e^{\left(\frac{-\zeta \pi }{\sqrt{1-{\zeta }^2}}\right)}$$对于二阶欠阻尼系统，1%对应的建立时间 $T_s$ ，10%~90%对应的上升时间 $T_r$ ，超调对应的 $Mp$ ,与阻尼比和自然频率相关，表示如下：
$$T_s\approx \frac{4.6}{\zeta {\omega }_n}$$$$T_r\approx \frac{1.8}{{\omega }_n}$$$$\zeta =\frac{-\ln (Mp)}{\sqrt{{\pi }^2+{\ln }^2(Mp)}}$$
过阻尼系统
如果 $\zeta >1$ ，则系统属于过阻尼系统，两个极点的实部都是负数，因此，系统是稳定的，不会振荡。过阻尼系统的阶跃响应和零极点图如下所示：

zeta = 1.2;

G2 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G2)
axis([-20 1 -1 1])

step(G2)
axis([0 1.5 0 1.5])

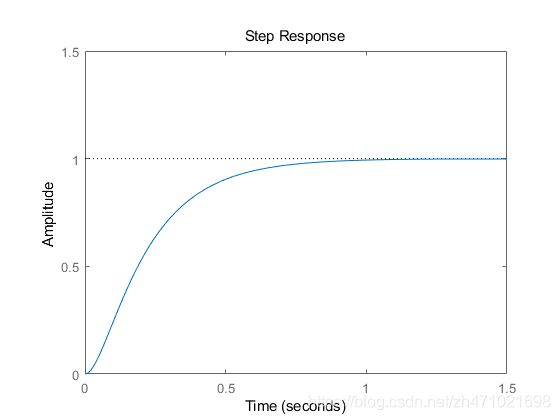
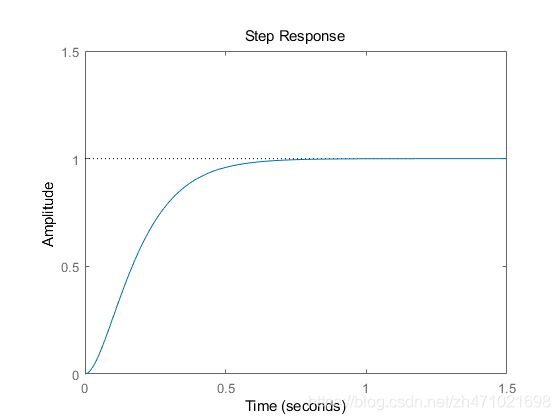
临界阻尼系统
如果 $\zeta =1$ ，则系统是临界阻尼系统，两个极点相等并都在实轴上， $s_p=-\zeta {\omega }_n$，对于规范的二阶系统，当系统处在临界阻尼时，可实现最快的建立时间。现在，将阻尼比设置为1，然后重新绘制阶跃响应曲线和零极点图：

zeta = 1;

G3 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G3)
axis([-11 1 -1 1])

step(G3)
axis([0 1.5 0 1.5])

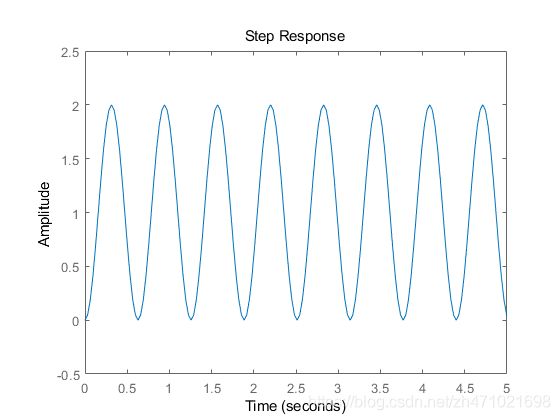
无阻尼系统
如果 $\zeta =0$，则系统是无阻尼系统，在这种情况下，极点都在虚轴上，因此，系统是稳定的，阶跃响应会无限振荡。

zeta = 0;

G4 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G4)
axis([-1 1 -15 15])

step(G4)
axis([0 5 -0.5 2.5])

伯德图
我们在下面显示了二阶系统所有阻尼条件的伯德幅值图和相位图：

bode(G1,G2,G3,G4)
legend('underdamped: zeta < 1','overdamped: zeta > 1','critically-damped: zeta = 1','undamped: zeta = 0')

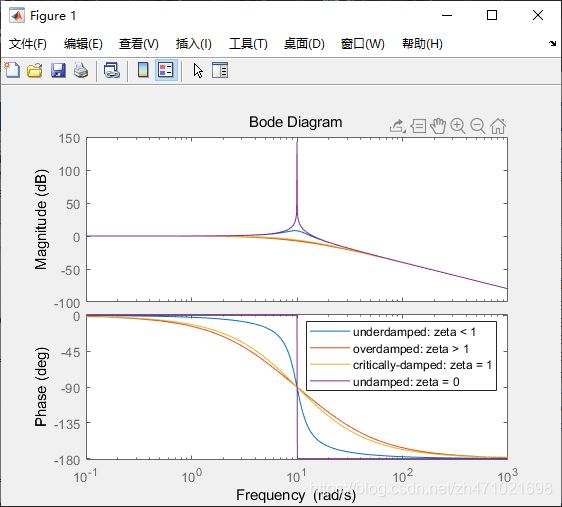
二阶系统的伯德图的幅值在范围内是以-40dB的速度下降，而相对的相位从0到-180度变化，对于阻尼不足的系统，我们还会在自然频率附近看到一个共振峰， ${\omega }_n$ = 10 rad/s，峰的大小和锐度取决于系统中的阻尼，并通过以下定义的品质因数(即Q因子)来表征。Q因子是信号处理中的重要属性。
$$Q=\frac{1}{2\zeta }$$