pytorch学习笔记3 求导
注：本文是笔者结合自己阅读和使用pytorch的经验，又系统学习了一遍https://github.com/chenyuntc/pytorch-book的过程中，将自己认为有必要掌握和记住的知识整理成的学习笔记，并非系统的教程，主要目的是为了方便自己梳理、记忆知识，以及方便有相同需求的读者查阅某些知识。
计算图
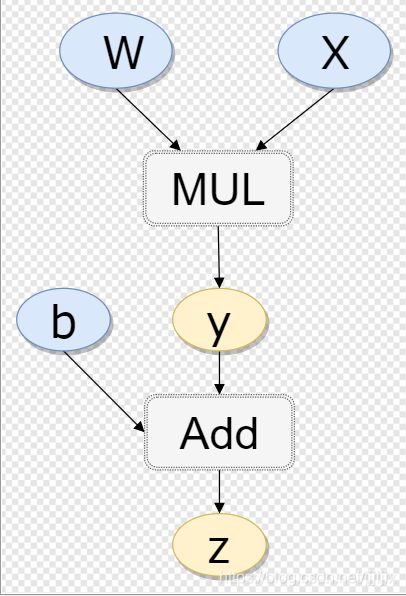
对于
，其计算图表示如下
关于计算图，有以下两点：
(1)计算图中有两种节点，变量（椭圆形）和操作（矩形），计算图必须要求与“变量”相连的一定是“操作”，与“操作”相连的一定是“变量”。假如例子里没有
，直接定义成
，计算图还是长现在这样子，只是被一个虚拟节点代替了。这样比较严格地定义计算图的形式，是为了后面好理解。
(2)计算图本质上是个树结构，因此后面我们会用根、叶子、子节点等用词进行描述
tensor.requires_grad
对于pytorch中的变量（也就是tensor），可以用requires_grad来表示其是否可以计算对它的梯度。有两点需要注意：
1、tensor的requires_grad属性默认为False
2、对于计算图中的存在父子关系的一对变量（先不考虑他们之间的“操作”节点）节点，比如例子里的y和w，如果父节点的requires_grad为False，子节点的requires_grad为True，那么因为子节点的梯度计算依赖于父节点，此时父节点的requires_grad会被自动设置为True
tensor.grad
反向传播之后tensor的梯度。注意三点：
1、求得的某个tensor x的梯度，一定与x是同形状的
2、pytorch中，只有requires_grad为True的叶子节点上的变量可以输出其梯度，非叶节点变量不能直接查看.grad属性
3、计算图建好之后叶子节点的梯度不会自动被求出来，此时访问x.grad得到的是None；只有对根节点调用.backward()方法后才能得到叶子节点的梯度
In [1]: x = t.randn(1, requires_grad=False)
In [2]: w = t.randn(1, requires_grad=True)
In [3]: b = t.randn(1, requires_grad=True)
In [4]: x, w, b
Out[4]: (tensor([-0.8750]), tensor([0.9619], requires_grad=True), tensor([0.3967], requires_grad=True))
In [5]: z.backward()
In [6]: w.grad, b.grad, x.grad, y.grad
Out[6]: (tensor([-0.8750]), tensor([1.]), None, None)tensor.grad_fn
返回的是一个函数的地址。那么这个函数是什么？
假如是tensor x调用的该属性，若x是非叶节点，返回的是x向叶节点方向操作的反向传播函数，比如例子里y节点对应的函数就是MulBackward，即乘法操作的反向函数；若x是叶节点且x的requires_grad为True，则这个函数是None
#接上一段
In [7]: z.grad_fn, y.grad_fn
Out[7]: (, )
In [8]: w.grad_fn, x.grad_fn, b.grad_fn
Out[8]: (None, None, None) tensor.grad_fn.next_functions
1、.next_functions属性的所有者不是“变量”节点（tensor），而是计算图中的“操作”节点。因此，对于tensor.grad_fn这个函数的地址，也就是“操作”节点，我们可以调用它的.next_functions属性。
2、"操作"节点的.next_functions属性，是一个二维的tuple，形式为( (函数1， int数1)，(函数2，int数2), ..., (函数N，int数N) )。我们以例子中的ADD节点为例（也就是z.grad_fn）对函数1到函数N是什么进行说明：对于一个“操作”节点（z.grad_fn为例），其所有的N个“变量”子节点（b节点、y节点）对应的反向传播时的操作节点（AccumulateGrad、MulBackward，注意，在.next_functions中，叶子节点如果requires_grad为True，该节点会有一个叫做AccumulateGrad的反向传播节点；如果叶子节点requires_grad为False，则该节点的反向传播节点为None）
# 接上一段
In [9]: z.grad_fn.next_functions
Out[9]: ((, 0), (, 0))
In [10]: y.grad_fn.next_functions
Out[10]: ((, 0), (None, 0)) tensor.backward()
对tensor x调用.backward()方法后，将以x作为计算图的根节点，对整个计算图进行反向传播，得到图中“变量”节点的梯度。.backward()方法有很多注意点：
1、grad_tensors参数：如果调用.backward()方法的tensor x是一个标量，grad_tensors参数可以不指定；但是如果x不是标量，需要传入一个全1的向量说明形状。先放一个例子，然后说明为什么要这样。
In [1]: tensor1 = t.randn(1, requires_grad=True)
In [2]: tensor2 = t.randn(1, requires_grad=True)
In [3]: tensor3 = tensor1 + tensor2
In [4]: tensor3.backward() # 调用后完成反向传播
In [5]: tensor4 = t.randn(2, 2, requires_grad=True)
In [5]: tensor5 = t.randn(2, 2, requires_grad=True)
In [6]: tensor6 = tensor4 + tensor5
In [7]: tensor6.backward() # 报错
In [8]: tensor6.backward(t.ones(2, 2)) # 调用后完成反向传播计入调用.backward()的节点为tensor x，其实grad_tensors参数表示的是
，当x是标量时，就是自己对自己求导值为1；但是x是个多维tensor时，的定义是不知道的（数学上没有 矩阵对矩阵 求导的严格定义），我们需要传入一个全1的tensor给grad_tensors参数作为，告诉程序我希望如何定义。在上面的例子里，我定义了形状为(2,2)的tensor6对自己求导的结果依然是(2,2)的全1矩阵，即对应位置上的元素对自己求导。事实上，我们也可以认为tensor6对自己求导的结果形状是(4, 4)，即每个位置对所有位置求导的结果一共4*4个，全部被记录下来；类似的，我们可以对求导的结果又非常多种的定义。
2、retain_graph参数：
（1）当计算图构建时（即前向传播时），会将“变量”子节点中的值存到buffer中，供其父节点对应的“操作”节点反向传播时使用。比如例子中，w和x的值都将放入buffer中，因为MUL操作在反向传播的过程中需要w和x的值。
（2）retain_graph默认为False，也就是在默认情况下，调用.backward()方法时，在反向传播求出所有梯度后，会将buffer清空。没有了buffer中的数据，此时不能再次求梯度。也就是说，当retain_graph为False时，建好计算图后，一个tensor只能调用一次.backward()方法。
（3）如果retain_graph为True，那么调用.backward()反向传播时不会清空buffer，此时就可以再次调用.backward()，多次调用.backward()后，叶子节点的梯度是每一次求得的梯度之和。
torch.no_grad()
上面说过，在计算图建立的同时，为了方便后续反向传播时梯度的计算，“变量”节点的值会被存到buffer中。这会带来一个问题就是，每一个变量都会存在两份，占用内存/显存的大小也会是不存储这些值时的两倍。在一些情况下，不需要进行反向传播（比如预测，以及一些特殊的任务），此时如果在torch.no_grad()的域中建立计算图，就不会把值存储在buffer中，当然此时也不能使用反向传播。
with t.no_grad():
x = t.ones(1)
w = t.rand(1, requires_grad = True)
y = x * w