hdu-1003 or 最大子序列和(四种解题方法)

首先，自己的第一想法是 找出两个相邻元素和最大的两元素，然后分别从左右再计算。
后来才知道错了= = ||。
（下面算法只是找到了最大和，未找元素下标）

1. 复杂度为O(N * N * N)的算法，也是最暴力的解法

int maxsubseqsum(int *list,int n)
{
	int i,j,k;
	int thissum,maxsum=0;
	for(i=0;imaxsum)
			{
				maxsum=thissum;
			}
		}
	}
	return maxsum;
}

2. 在上述算法进行优化。上面有许多无用计算，我们可以把计算过的保存起来。复杂度为O(N*N)

int maxsubseqsum(int *list,int n)
{
	int i,j,k;
	int thissum,maxsum=0;
	for(i=0;imaxsum)
		{
			maxsum=thissum;
		}
	}
	return maxsum;
}

3. 分治算法，复杂度
   记总的的为T(N)=2T(N/2)(两个递归)+O(N)(跨界求和的循环)，然后展开，为2^
   kT(N/2^k)+kO(N),
   直到2^k=N,所以有T（N）=NT(1)+lgN(就是lnN)o(N)=O(NlgN);

这个递归我理解了很长时间，哎。

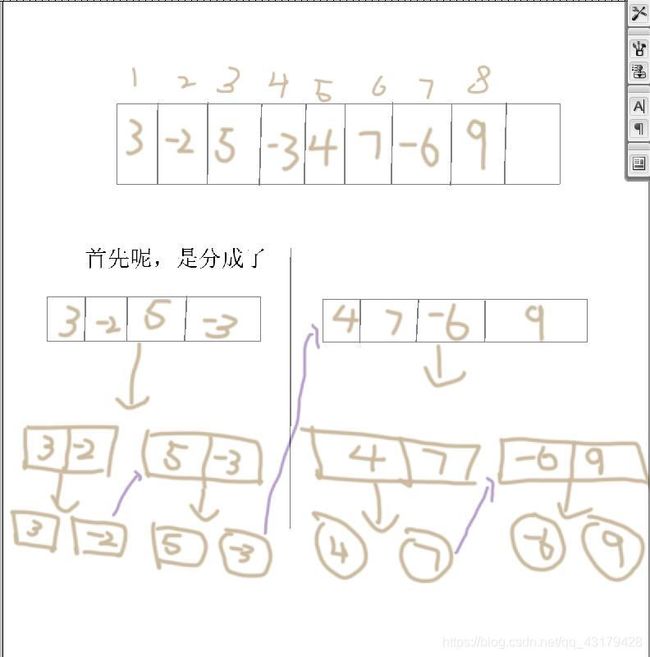
就用这个例子吧
首先center=4;

(list,1,4)=8
{
		(list,1,2)=3
		{
			(list,1,1)=3;
			(list,2,2)=0;本是-2
		}

	(list,3,4)=5
	{
		(list,3,3)=5;
		(list,4,4)=0;本是-3
	}
}


(list,5,8)=14
{
	(list,5,6)=11
	{
		(list,5,5)=4;
		(list,6,6)=7;本是-2
	}
	(list,7,8)=9
	{
		(list,7,7)=0,本是-6;
		(list,8,8)=9;
	}
}
接下来就是跨段和
从4 3 2 1 和 5 6 7 8分别计算，所得maxleft+maxright=17;
用max(8,14,17),故为17

int max3(int a,int b,int c)
{
	return a>b?a>c?a:c:b>c?b:c;
	/*
		if a>b
		{
			if a>c
				max=a
			else
				max=c
		}
		else
		{
			if b>c
				max=b
			else
				max=c
		}
	
	*/ 
}
int divid_and_conquer(int *list,int left,int right)
{
	int max_left_sum,max_right_sum;
	int max_left_border_sum,max_right_border_sum;
	int left_border_sum,right_border_sum;
	int center,i;
	if(left==right)
	{
		if(list[left]>0) return list[left];
		else return 0;
	}
	max_left_sum=divid_and_conquer(list,left,center);
	max_right_sum=divid_and_conquer(list,center+1,right);
	
	分段求和 
	max_left_border_sum=left_border_sum=0;
	for(i=center;i>=left;i--)
	{
		left_border_sum+=list[i];
		if(left_border_sum>max_left_border_sum)
			max_left_border_sum=left_border_sum;
	}
	
	扫描右边 
	max_right_border_sum=right_border_sum=0;
	for(i=center+1;i<=right;i++)
	{
		right_border_sum+=list[i];
		if(right_border_sum>max_right_border_sum)
			max_right_border_sum=right_border_sum;
	}
	return max3(max_left_sum,max_right_sum,max_right_border_sum+max_left_border_sum);
}

4. 在线算法，复杂度为O(N),我们可以简单证明为最快的算法：所有数据必须要处理一遍，所以O(N)的算法最快，即只处理一遍数据。

int maxsubseqsum(int *list,int n)
{
	int thissum,maxsum;
	thissum=maxsum=0;
	for(int i=0;imaxsum)
			maxsum=thissum;
		else if(thissum<0)
			thissum=0;//一旦出现负的，我们就不需要在往下加了
		
	}
	return maxsum;
	
}