介绍
Kmeans聚类算法:K均值聚类
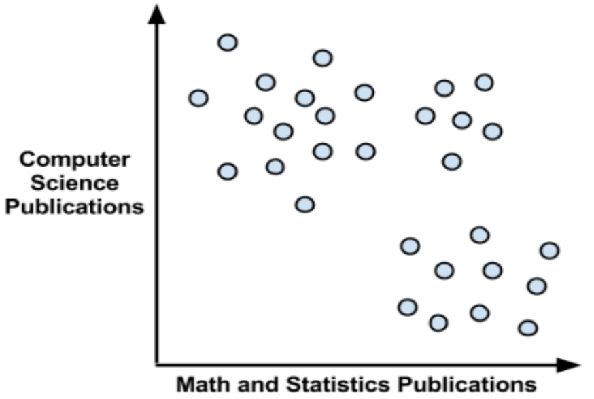
聚类:给事物打标签,寻找同一组内的个体之间的一些潜在的相似模式。力图找到数据的自然分组kmeans
学完Kmeans算法后,你将理解:
Kmeans算法的基本原理
如何将聚类应用到现实世界的市场细分任务,例如青少年社交媒体用户的市场细分
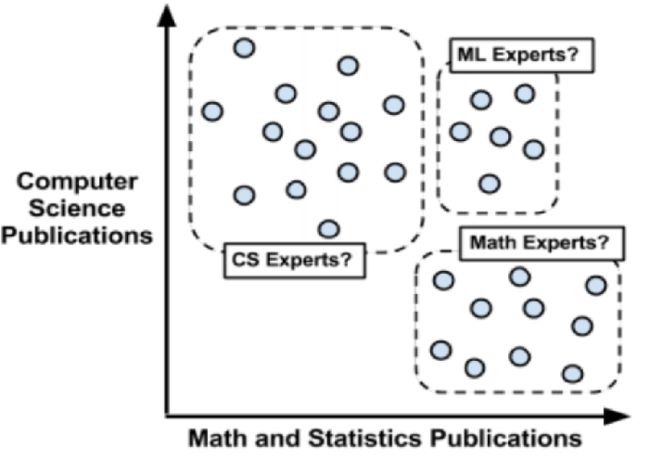
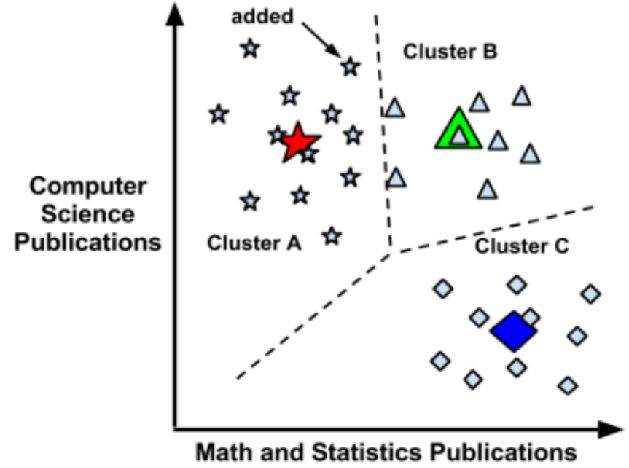
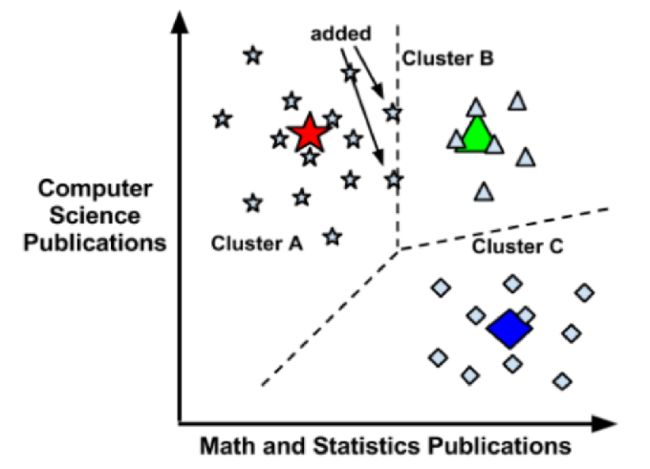
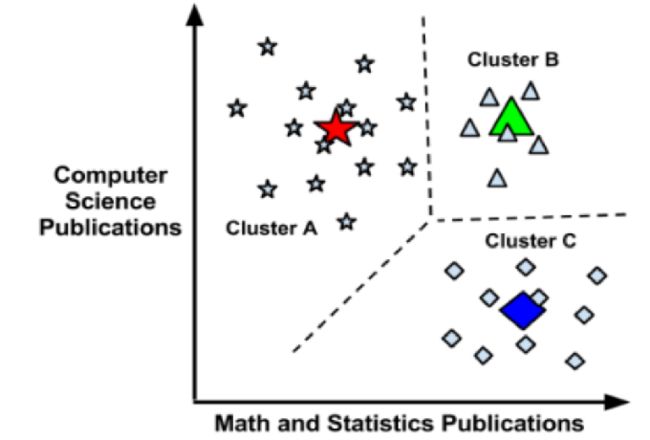
聚类是一种无监督的机器学习任务,它可以自动将数据划分成类cluster。因此聚类分组不需要提前被告知所划分的组应该是什么样的。因为我们甚至可能都不知道我们再寻找什么,所以聚类是用于知识发现而不是预测
聚类原则是一个组内的记录彼此必须非常相似,而与该组之外的记录截然不同。所有聚类做的就是遍历所有数据然后找到这些相似性
使用距离来分配和更新类
使用距离来分配和更新类
探究距离测度
欧氏距离测度(EuclideanDistanceMeasure)
平方欧氏距离测度(SquaredEuclideanDistanceMeasure)
曼哈顿距离测度(ManhattanDistanceMeasure)
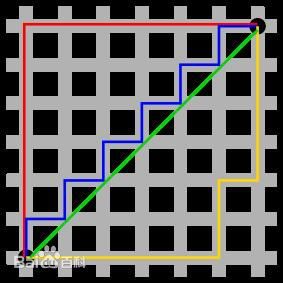
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离
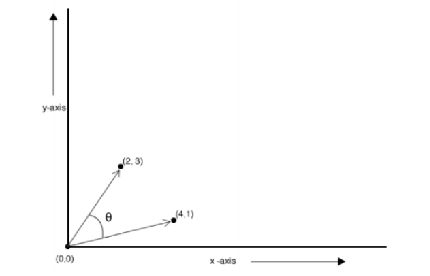
余弦距离测度(CosineDistanceMeasure)
谷本距离测度(TanimotoDistanceMeasure)
同时表现夹角和距离的距离测度
加权距离测度(WeightedDistanceMeasure)
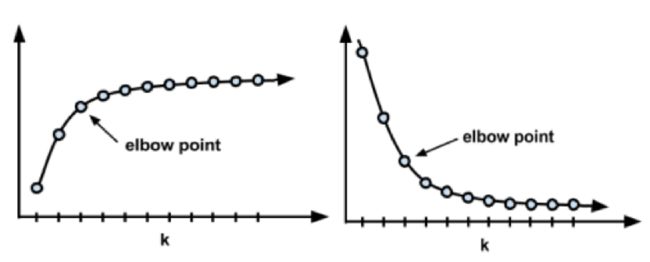
选择适当的聚类数
Kmeans算法思想以总结
算法思想:
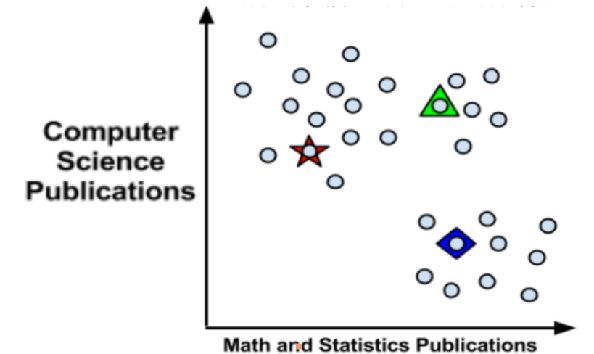
以空间中K个点为中心进行聚类,对最靠近他们的对象归类,通过迭代的方法,逐次更新各聚类中心的值,直到得到最好的聚类结果
算法流程总结:
1、适当选择k个类的初始中心
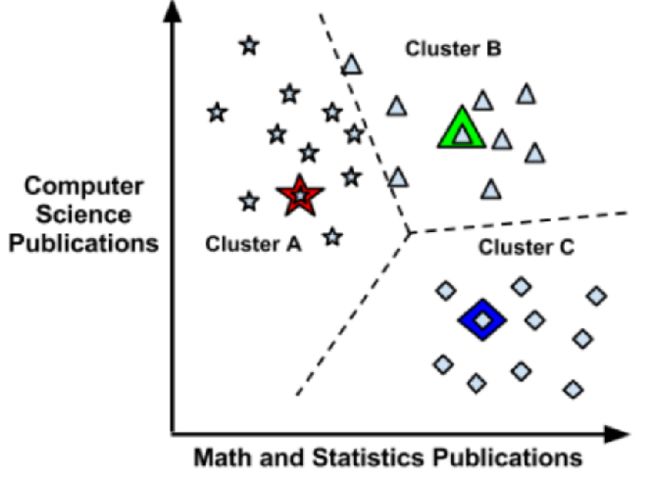
2、对任意一个样本,求其到各类中心的距离,将该样本归到距离最短的中心所在的类
3、利用均值等方法更新每个聚类的中心值
4、重复2,3的迭代,直到k个中心点值保持不变,则迭代结束,否则继续迭代
Kmeans算法的缺陷
聚类中心的个数K 需要事先给定,但在实际中这个 K 值的选定是非常难以估计的,很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适
Kmeans需要人为地确定初始聚类中心,不同的初始聚类中心可能导致完全不同的聚类结果。(可以使用Kmeans++算法来解决)
Kmeans++算法的介绍
从输入的数据点集合中随机选择一个点作为第一个聚类中心
对于数据集中的每一个点x,计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大
重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法
数据实验:
代码
# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 建立12*12英寸 新的图像
plt.figure(figsize=(12, 12))
n_samples = 150
random_state = 170
'''
make_blobs函数是为聚类产生数据集 , 产生一个数据集和相应的标签
n_samples:表示数据样本点个数,默认值100
n_features:表示数据的维度,特征,默认值是2
centers:产生数据的中心点,默认值3个
shuffle :洗乱,默认值是True
random_state:官网解释是随机生成器的种子
'''
# x返回的是向量化的数据点,y返回的是对应数据的类别号
x, y = make_blobs(n_samples=n_samples, random_state=random_state)
print('x=', x, type(x), 'y=', y, type(y))
# 使用KMeans去聚类,返回聚好的类别集合, n_clusters聚合成几类
y_pred = KMeans(n_clusters=3).fit_predict(x)
print("y_pred : ", y_pred)
# subplot 绘制多个子图,221 等价于2,2,1 表示两行两列的子图中的第一个
plt.subplot(221)
# scatter 绘制散点图 ,c 指定颜色
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.title("kmeans01")
transformation = [[0.60834549, -0.63667341],
[-
0.40887718, 0.85253229]]
# numpy.dot 矩阵相乘
# a1= [[1,2]
# [3,4]
# [5,6]]
# a2= [[10,20]
# [30,40]]
# a1*a2 = [[1*10+2*30,1*20+2*40]
# [3*10+4*30,3*20+4*40]
# [5*10+5*30,6*20+6*40]
# ]
X_aniso = np.dot(x, transformation)
y_pred = KMeans(n_clusters=3).fit_predict(X_aniso)
plt.subplot(222)
# # s 设置点的大小,s=8
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("kmeans02")
# vstack 是合并矩阵,将y=0类别的取出500行,y=1类别的取出100行,y=2类别的取出10行
X_filtered = np.vstack((x[y == 0][:500], x[y == 1][:100], x[y == 2][:200]))
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
plt.subplot(223)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("kmeans03")
dataMat = []
fr = open("testSet.txt", "rb")
for line in fr.readlines():
if line.decode("utf-8").strip() != "":
curLine = line.decode("utf-8").strip().split('\t')
fltLine = list(map(float, curLine))
dataMat.append(fltLine)
dataArray = np.array(dataMat)
print("dataArray type = %s"% type(dataArray))
# 调用Scikitlearn中的KMeans
# KMeans 中参数 init='k-means++' 默认就是k-means++ 如果设置为'random'是随机找中心点
y_pred = KMeans(n_clusters=5).fit_predict(dataArray)
plt.subplot(224)
plt.scatter(dataArray[:, 0], dataArray[:, 1], c=y_pred)
plt.title("kmeans04")
plt.savefig("./kmeans.png")
plt.show()
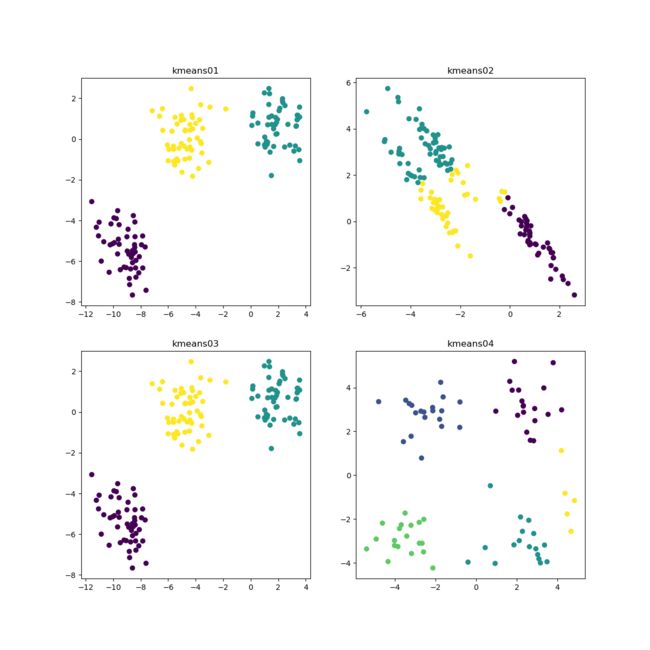
我们做了四组数据
第一组数据,第二像限(左上角),是原始数据,通过make_blobs生成150个数据,默认产生有三个中心点。然后通过使用KMeans去聚类,返回聚好的类别集合, n_clusters聚合成几类,我们手工设置成3。 将聚合的结果打印在第二像限, 得出的结果也是十分靓仔。
第二组数据,第一像限(右上角)的数据是通过上一组数据来矩阵相乘得来的。我们看到把数据拉“长”后, 分布预测似乎有点不尽人意。
第三组数据,第三像限(左下角)。vstack 是合并矩阵,将y=0类别的取出500行,y=1类别的取出100行,y=2类别的取出10行。最后得出的结果也是尽如人意。
第四组数据, 第四像限(右下角图)。这是我们之前的随机数据,比刚才的测试数据要零散, 最后我们通过肉眼分析出5类, 得出的结果也是我们想要的结果。
总结
KMeans这个方法基本上可以很好地帮我们分出类来, 但对于一些分布较为奇特, 想第二组数据的椭圆形时,这个方法就显得不太理想。