基于FPGA的FFT

    在MATLAB中进行波束形成的程序设计和仿真之前，要合理的选择参数，并根据仿真的结果对所设置的参数进行调整，例如滤波器的系数，滤波器滚降系数，FFT变换长度等，从而使得系统的仿真结果达到较优的性能。

  ·接收阵参数：

    接收阵的基元数为64，基元间距（为信号的波长），为2.4mm；

  ·混频信号参数与正余弦混频信号的产生：

    混频信号的中心频率为1.2MHz，混频信号的中心频率越接近输入信号的中心频率，则对采样率的要求越低，而且低通滤波器的截止频率也更小，从而更好的抑制噪声。产生的正弦余弦混频信号的长度为40点。通过混频信号将各个阵元接收的时间序列与混频信号对应点相乘。

  ·低通滤波器参数：

    低通滤波器的阶数为16，通带截止频率为58kHz，阻带截止频率为140kHz。通过matlab中自带的firpm函数进行滤波器的设计，最后得到的滤波器系数为：

    0，

    -0.0052，

    0，

    0.0231，

    0，

   -0.0758，

    0，

    0.3066，

    0.4991，

    0.3066，

    0，

   -0.0758，

    0，0.0231，

    0，

   -0.0052，

   0

其波形如下图所示：

 

图1 低通滤波器系数

  ·采样频率参数

    采样频率为960kHz，在确定输入信号和混频信号的频率的条件下，得到的复移位边带信号的中心频率为65kHz，理论上要求的采样频率大于65kHz。但是考虑到要在信号脉宽的时间范围之内采集到足够的数据完成至少一次波束形成，采样率不可以选取过小的值。而且为了减少噪声的干扰，通常要取几组输出的平均作为最终的波束输出，因此，需要进一步提高输入的数据量。如果每个CW脉冲最终得到两组波束图，而每组波束图是取十组中间结果的平均值得话，在低通滤波器阶数为15的情况下，则至少每路信号在脉宽时间内采集35个点，所有采样率最小为525kHz。取采样频率为960kHz，是混频信号频率的0.8倍，通过混频信号采样之后，大大简化了乘法运算。

    在本文下一章节，将对算法的系统性能进行仿真分析。

X.2.1 系统的角度分辨率分析

    波束形成系统的角度分辨率分析，即算法对不同角度的分辨精度的分析，在本章节，我们通过设计如下仿真参数进行仿真分析，通过MATLAB仿真分析移相波束形成的角度分辨率。

表1角度分辨率分析仿真参数

	参数名称	参数值
1	入射角度	[0.1:0.1:45]
2	中心频率	1.25MHz
3	脉宽	66.7us
4	阵元数	64
5	滤波器的阶数	16
6	通带截止频率	58kHz
7	阻带截止频率	140kHz
8	信噪比	24db

    将入射角的角度从1度抓紧变化到60度，通过系统得到每个入射角度对应的角度计算值，然后分析理论值和实际值得差作为角度分辨率的精度。通过仿真，得到如下的仿真结果：

    从图2的仿真结果可知，当入射角的角度从0.01逐渐增加到45度的时候，理论值和计算角度的误差均在0~0.2度之间，这说明本文所设计的相移波束形成算法具有较好的性能，符合实际的工作需求。

X.2.2 噪声对算法精度的影响分析

    本节，我们主要分析噪声对波形形成算法精度的影响，这里，我们分别设置信噪比SNR为-30db，-25db，...，20db，入射角设置为30度（其余参数和上一节做相同的设置）依次对着几组SNR值进行仿真分析。

    通过仿真，可以得到如下的仿真结果：

 

图3角度分辨率误差仿真图

    从图3的仿真结果可知，随着信噪比SNR值得增加，理论值和实际计算值得误差越来越小，当SNR小于-15的时候，系统的误差较大，当SNR逐渐增加直到达到-7左右的时候，计算值误差快速降低，当SNR达到20的时候，系统的误差将在0.1以内，满足实际的需求。

    进一步，我们来分析一下不同的FFT变换长度，其对应的误差变换曲线。分别设置FFT变换长度为16，32，64，128，通过仿真，得到如下的误差变换曲线。

 

图4不同FFT变换长度的角度分辨率误差仿真图

    从图4的仿真结果可知，当FFT变换长度越长的时候，系统的计算误差越小，从上图的结论可知，当SNR为0的时候，当FFT长度为16，角度误差值为1.0188度，当FFT长度为32，角度误差值为0.4550度，当FFT长度为64，角度误差值为0.1975度，当FFT长度为128，角度误差值为0.0613度。而当FFT长度为256的时候，系统的性能得到显著的提升，在SNR为-10的时候，其性能已经达到0.01以内。由此可见，选择合适的FFT变换长度，可以有效提升系统的性能。

    在本课题中，综合考虑算法的仿真速度需求以及性能需求，我们选择FFT变换的长度为256。

X.2.3系统的的角度范围分析

    本节，我们主要对系统的角度分辨范围进行仿真分析，将信号入射角从0度逐渐增加到80度，信噪比SNR设置为10db，FFT变换长度设置为64，然后分析各个入射角对应的计算误差，从而分析出其中误差较小的入射角范围，即为算法的角度分辨范围。

    从图5的仿真结果可知，当入射角度逐渐增加的时候，对应的算法误差逐渐增加，当入射角度大于70度的时候，误差快速增加，因此从图5的仿真结果可知，算法有效的计算角度为0~70度，考虑到算法的对称性，实际算法的有效计算角度为-70~70之间，当在这个角度范围之外的时候，系统的误差较大。

    通过上面几个章节的分析，我们大致对本系统的性能有了初步的了解，在本章的后面几个小节，我们将对FPGA系统进行资源分析和性能分析。

X.2.4 基于FPGA的系统硬件资源占用分析

     根据系统的基本结构图，我们进行系统的FPGA实现。

    从图6的基本构架可知，移相波束形成FPGA系统，其主要包括控制模块，混频器，LPF低通滤波器，RAM存储器，MUX选择器，FFT傅里叶变换模块以及模计算模块。

  ·控制模块

    控制模块其主要功能是控制各个模块的时序和RAM模块的读写地址。

  ·混频器

    混频模块，产生正弦信号和余弦信号，然后将正弦和余弦信号同输入信号进行相乘，完成输入信号的混频功能，这个模块的资源占用如下图所示：

图7 混频模块资源占用情况

    从图7的综合结果可知，混频模块共使用3298个逻辑单元以及200个乘法器模块。

  ·LPF低通滤波器

    低通滤波器的设计，主要通过一个移位寄存器和乘法器，将延迟后的输入数据和系数相乘累加，然后输出滤波结果。在FPGA系统中，滤波器系数需要通过量化后才能使用。这个模块的资源占用如下图所示：

图8 低通滤波器模块资源占用情况

    从图8的综合结果可知，低通滤波器模块共使用144个逻辑单元。

  ·RAM存储器

    在本系统中，通过两个RAM模块实现乒乓RAM结构，对滤波结果进行缓存，由于FFT是对所有基元在同一时刻的信号进行计算的，所以要等所有基元的信号进行混频，滤波后才能进行FFT变换。因此，缓存模块式一个十分重要的模块。采用乒乓结构进行缓存，能够使系统形成流水线结构，并使得运算不间断。每个RAM均为双口RAM，双口RAM将RAM的空间分为两个部分，保存信号的实部和虚部。这个模块的资源占用如下图所示：

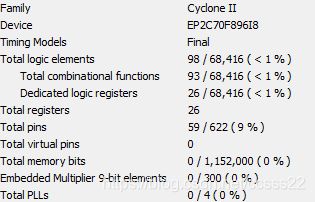
图9 RAM模块资源占用情况

    从图9的综合结果可知，RAM模块共使用26个逻辑单元。

  ·FFT傅里叶变换模块

    根据前面的分析，FFT长度选择256，整个FFT模块，基于基2蝶形运算单元进行设计，FFT模块的管脚有CLK（系统时钟信号），RST（复位信号），ED（FFT模块使能信号），START（FFT起始信号），SHIFT（转移信号），DR（输入实部），DI（输入虚

部），RDY（计算开始信号），OVF1（溢出信号1），OVF2（溢出信号2），ADDR（输出地址），DOR（输出实部），DOI（输出虚部）。这个模块的资源占用如下图所示：

图10 FFT模块资源占用情况

    从图10的综合结果可知，RAM模块共使用5127个逻辑单元，8个乘法单元。整个移相波束形成系统的资源占用情况如图11所示：

图11 移相波束形成系统资源占用情况

    从上面的综合结果可知，当使用EP2C70F896I8芯片的时候，其资源占用情况如下：

  ·总体逻辑使用15270个，占总的资源的22%；

  ·寄存器使用8521个，占总的资源的12%；

  ·外部IO口使用178个，占总IO口的29%；

  ·总体bit存储器使用42464bits，占总的4%；

  ·嵌入式乘法器使用112个，占总体的37%。

    从图11的综合结果可知，本系统采用的设计方法，最后资源整体占用率在20%左右，所以资源占用较少，符合系统设计的时候低逻辑消耗的需求。

X.2.5 基于FPGA的系统仿真分析

    本节，我们将对FPGA系统进行详细的仿真分析，首先对移相波束形成系统的几个主要模块进行仿真分析。然后对FPGA系统的整体系统进行分析。

    混频器的正弦和余弦输出仿真结果如下图所示：

图12混频器输出仿真

    从图12可知，混频器的输出正弦和余弦信号，其每个周期包含16个采样点，即时钟每过16个采样周期后输出一个周期的正弦和余弦。混频器的输出的载波和输入相乘完成混频，其中余弦输出和输入信号相乘得到实部，正弦输出和输入信号相乘得到虚部。然后将这两个数据用于系统后一级的滤波处理。

    低通滤波器的仿真结果如下下图所示：

图13低通滤波器的输出仿真

    从图13的仿真结果可知，FPGA的低通滤波器输出基本和MATLAB的输出一致，信号通过低通滤波器之后，输出边缘带滚降的滤波效果，本系统低通滤波器的滚降系数为0.5。低通滤波器的输出信号将进入双口RAM进行FFT变换准备。

    FFT的仿真结果如下图所示：

 

图14 FFT变换的输出仿真

    从上图的仿真结果可知，与MATLAB中计算结果基本一致。图14中O_I_fft为FFT变换后的实部输出，O_Q_fft为FFT变换后的虚部输出。

    将FFT的实部和虚部取模后得到图15的仿真结果：

 

图15 取模的输出仿真

    上图的仿真是以5度入射的正弦信号作为仿真激励进行仿真的，它与MATLAB中的计算结果基本一致。

    将上述的仿真结果放大，可以看到：

 

图16 整体仿真结果图

    将上面的仿真结果和实际的MATLAB输出进行对比，两者的误差在0.03度左右，对于入射角度为5度的情况下，这个误差在0.6%左右。由此可见，FPGA系统基本达到实际的指标需求，其中存在的误差是由于位宽截取，定点仿真过程所导致的误差。

X.3本章总结

    本章，我们根据所设置的参数对相移波束形成进行性能的仿真，首先通过MATLAB仿真，分别对系统的角度分辨率，噪声对算法精度的影响以及系统的角度分辨范围进行了分析。通过仿真可知系统的角度分辨误差在在0~0.2度之间，随着信噪比SNR值得增加，理论值和实际计算值得误差越来越小，当FFT变换长度越长的时候，系统的计算误差越小。最后通过仿真得到，当入射角度范围在-70~70之间的时候，计算的误差较小，在这个范围之外的时候，系统的误差较大。然后对FPGA的系统进行了资源占用分析和性能分析，通过分析可知，通过FPGA设计的移相波束形成系统达到了MATLAB仿真效果。