图像水波纹特效原理分析和实现

 　　前段时间注意到一些软件上有图像的水波纹特效，似乎很炫，想深入了解下该效果的具体原理与实现方式，上网搜了不少些资料，都讲得不清不楚，没办法只能靠自己了。花了一整个下午先去复习了高中物理的波的知识，试着自己来推导原理并实现了下。下面的推导是我根据一些资料以及自己分析出的，如有错误，望请指出。上张效果图先：

 

基本原理 

---

　　水波效果反映到图像上，则是像素点的偏移。因此对图像的处理就如同图像缩放一样，对于输出图像的每个点，计算其对应于原始输入图像的像素点，通过插值的方法即可计算其颜色值。 

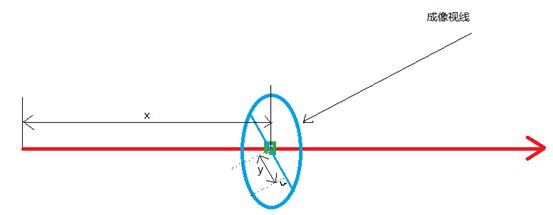
　　先说下关于水波的基础知识。波的传播方向与质点振动方向垂直的为横波，相同则为纵波，水波是横波和纵波的叠加，因此水波在传播时，每个质点存在水平运动和上下运动，合起来就是一个椭圆的圆周运动，如下图的蓝色椭圆。 

　　如图，红轴表示水面，对于图像来讲，只有在垂直于成像视线的方向（图中蓝色线段）产生的运动才会引起像素的偏移，而平行于实现方向则可以忽略。那么对于某个点x，其运动轨迹上的每个点都可以分解为与视线平行和垂直的2个方向上的位移，我们只要计算出垂直视线的位移y即可计算出水波导致像素点的偏移位移。 

 　　假定水波是平面简谐波，则能得到其波动方程

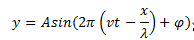 　　式中，A是振幅，v是波速，t是时间，lamda是波长， x为距离波源的距离，phi为初始相位。但是随着时间的推移和波的传播，其能量会衰减，即其振幅会随着时间和位置衰减，则上面的公式需修改为：

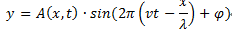 　　函数表征了水波能量的衰减情况，因此该函数必须是关于x和t的单调递减函数，实际水波的递减是什么规律我不清楚，但这里自行设定一个即可，一般的衰减函数有线性衰减和指数衰减，具体好坏只要实验结果才具有说服力。 

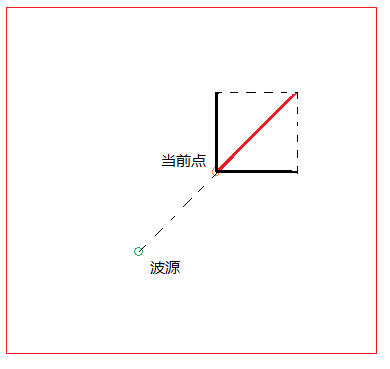
　　一个波源可以由波长，波速，初始相位和振幅唯一确定，因此对于某个时刻的某个点，我们可以计算出其位移。另一方面，水波是向四面八分同时传播的，对图像坐标系来看，每个点的位移都可以分解为水平与垂直位移，从而就可以确定像素点的精确偏移了。当然，对于多个波源，可以分别考虑，每个点的位移是所有波源引起的位移和。

 

水波纹特效具体实现 

---

 下面就是具体实现了，这个效果实现应该比较简单的。首先有一个波源对象。

 1 typedef unsigned char BYTE;

 2 #define PI 3.1415926

 3 //一个波源

 4 class CWaveSource

 5 {

 6 public:

 7     CWaveSource(float f32Cx = 100.0f, float f32Cy = 100.0f, 

 8                 float f32MaxAmp = 20.0f, float f32Phase = -PI/2,

 9                 float f32WaveLen = 10.0f, float f32V = 1.0f);

10     ~CWaveSource();

11 

12     //该波源在当前时刻，x，y位置处的振幅

13     void GetAmplitude(int x, int y, float &f32ax, float &f32ay);

14 

15     //波传播到下一时刻，需修改相应的波的状态

16     bool Propagate();

17 

18 private:

19     float m_f32Cx;        //波源中心点坐标

20     float m_f32Cy;

21     float m_f32MaxAmp;    //t时刻中心点最大振幅，t=0最大

22     float m_f32InitPhase; //初始相位

23     float m_f32WaveLen;   //波长

24     float m_f32Velocity;  //波速

25     int   m_nTime;        //时间

26 

27     bool  m_bDisappear;   //该波源是否可以消失，随着时间变化，其能量衰减到很小的时候可以认为其消失了

28     float m_f32CurRadius; //当前时刻波的半径,用于节约计算量的变量

29 };

CWaveSource

这里面注释比较清楚，就不多说了。该对象对应的实现为：

 1 CWaveSource::CWaveSource(float f32Cx, float f32Cy, 

 2                          float f32MaxAmp, float f32Phase, 

 3                          float f32WaveLen, float f32V)

 4 {

 5     m_f32Cx = f32Cx;

 6     m_f32Cy = f32Cy;

 7     m_f32MaxAmp = f32MaxAmp;

 8     m_f32InitPhase = f32Phase;

 9     m_f32WaveLen = f32WaveLen;

10     m_f32Velocity = f32V;

11     m_nTime = 0;

12     m_bDisappear = false;

13     m_f32CurRadius = 1e-12;

14 }

15 CWaveSource::~CWaveSource()

16 {

17 

18 }

19 

20 bool CWaveSource::Propagate()

21 {

22     //下一个时刻

23     m_nTime++;

24     m_f32CurRadius += m_f32Velocity;

25     //考虑最大振幅随时间的衰减,这里的衰减函数可以自己设定

26     //只要振幅随着时间递减即可，最好能做到比较自然

27     m_f32MaxAmp /= 1.01f;

28 

29     //能量衰减到一定程度后，可以认为该波源已消失，通过返回让外面把它删掉

30     if(m_f32MaxAmp < 1e-3)

31     {

32         m_bDisappear = true;

33     }

34     return m_bDisappear;

35 }

36 

37 void CWaveSource::GetAmplitude(int x, int y, float &f32ax, float &f32ay)

38 {

39     f32ax = f32ay = 0.0f;

40     //波源已消失，防止上层未删掉，耗计算量

41     if(m_bDisappear) return;

42     //注：这里可以建一个表，图像区域每个点相对波源中心点位置是固定的，即是f32Dist固定

43     //那么位置对应的衰减系数就应该是固定的

44     //这样对于一个波源只需计算一次f32Dist和衰减系数r了

45     //此处为了代码的可读性，暂时不那样实现    

46     float f32Radius = m_f32CurRadius;

47     float f32Dx = (m_f32Cx - x);

48     float f32Dy = (m_f32Cy - y);

49 

50     float f32Dist = f32Dx * f32Dx + f32Dy * f32Dy;

51     if(f32Dist > f32Radius * f32Radius) return;

52 

53     f32Dist = sqrt(f32Dist);

54     //考虑当前点最大振幅随位置的衰减,这里的衰减函数也可以自己设定

55     float r = 1 - f32Dist / 1000.0f;//exp(-f32Dist/10);

56     float f32MaxAmp = m_f32MaxAmp * r;

57 

58     //计算当前点的振幅,每个点的相位在不停变化的 y = Acos(2*pi*(vt-x)/wavelen + phase)

59     float f32Temp = 2 * PI * (m_f32Velocity * m_nTime - f32Dist) / m_f32WaveLen + m_f32InitPhase;

60     float f32CurAmp = f32MaxAmp * sin(f32Temp);

61 

62     f32ax = f32CurAmp * ABS(f32Dx)/f32Dist;

63     f32ax = f32CurAmp * ABS(f32Dy)/f32Dist;

64 }

View Code

好了，这样一个波源就已经构造好了。对图像的水波特效处理对象如下：

  1 class CRippling

  2 {

  3 public:

  4     CRippling();

  5     ~CRippling();

  6     

  7     //增加一个波源，该函数最好能重载一个直接输波源参数的，这里暂时忽略

  8     void AddSource(CWaveSource &WaveSource);

  9     

 10     //当前已有的波源对图像进行处理

 11     void Process(BYTE *pu8Dst, BYTE *pu8Src, int nWidth, int nHeight, int nChannels = 1);

 12     

 13     //所有波源传播

 14     void Propagate();

 15 

 16 private:

 17     //获取当前时刻所有波源作用下，像素点x，y对应于原始图像的像素位置，返回到x，y中

 18     void GetPos(float &x, float &y);

 19 

 20     //获取图像亚像素值，采用双线性插值

 21     void GetSubPixel(BYTE *pu8Dst, BYTE *pu8Src, int nWidth, int nHeight, int nChannels, float x, float y);

 22 

 23     //波源相关信息,因为需要插入和删除故采用list管理，也可以使用数组或者其他数据结构

 24     list<CWaveSource> m_lWaveSrc;

 25 };

 26 

 27 CRippling::CRippling()

 28 {

 29 }

 30 

 31 CRippling::~CRippling()

 32 {

 33 }

 34 

 35 void CRippling::AddSource(CWaveSource &WaveSource)

 36 {

 37     m_lWaveSrc.push_back(WaveSource);

 38 }

 39 

 40 void CRippling::Process(BYTE *pu8Dst, BYTE *pu8Src, int nWidth, int nHeight, int nChannels)

 41 {

 42     int nRow, nCol;

 43     float x,y;

 44     for(nRow = 0; nRow < nHeight; nRow++)

 45     {

 46         for(nCol = 0; nCol < nWidth; nCol++)

 47         {

 48             x = nCol;

 49             y = nRow;

 50             GetPos(x, y);

 51             GetSubPixel(pu8Dst, pu8Src, nWidth, nHeight, nChannels, x, y);

 52             pu8Dst += nChannels;

 53         }

 54     }

 55 }

 56 

 57 void CRippling::Propagate()

 58 {

 59     //每个波源都需要传播

 60     list<CWaveSource>::iterator It = m_lWaveSrc.begin();

 61     while(It != m_lWaveSrc.end())

 62     {

 63         bool bDisappear = It->Propagate();

 64         //波源可以消失，则删掉

 65         if(bDisappear) It = m_lWaveSrc.erase(It); 

 66         else It++;

 67     }

 68 }

 69 

 70 void CRippling::GetPos(float &x, float &y)

 71 {

 72     //根据平面简谐波的特性，某个点的位移是所有波位移和

 73     float f32AmpX = 0;

 74     float f32AmpY = 0;

 75     list<CWaveSource>::iterator It = m_lWaveSrc.begin();

 76     while(It != m_lWaveSrc.end())

 77     {

 78         It->GetAmplitude(x, y, f32AmpX, f32AmpY);

 79         x += f32AmpX;

 80         y += f32AmpY;

 81         It++;

 82     }

 83 }

 84 

 85 void CRippling::GetSubPixel(BYTE *pu8Dst, BYTE *pu8Src, int nWidth, int nHeight, int nChannels, float x, float y)

 86 {

 87     //采用双线性插值，就实际效果来看，最近邻插值也可以的

 88     int x0 = x;

 89     int y0 = y;

 90     int x1 = x0 + 1;

 91     int y1 = y0 + 1;

 92 

 93     float wx1 = x - x0;

 94     float wy1 = y - y0;

 95     float wx0 = 1.0f - wx1;

 96     float wy0 = 1.0f - wy1;

 97 

 98     x0 = MAX(x0, 0);

 99     x1 = MAX(x1, 0);

100     y0 = MAX(y0, 0);

101     y1 = MAX(y1, 0);

102 

103     x0 = MIN(x0, nWidth-1);

104     x1 = MIN(x1, nWidth-1);

105     y0 = MIN(y0, nHeight-1);

106     y1 = MIN(y1, nHeight-1);

107     for(int i = 0; i < nChannels; i++)

108     {

109         u8 * pu8Y0 = pu8Src + y0 * nWidth * nChannels;

110         u8 * pu8Y1 = pu8Src + y1 * nWidth * nChannels;

111 

112         float sum_y0 = (pu8Y0[x0 * nChannels + i] * wx0 + pu8Y0[x1 * nChannels + i] * wx1);

113         float sum_y1 = (pu8Y1[x0 * nChannels + i] * wx0 + pu8Y1[x1 * nChannels + i] * wx1);

114         pu8Dst[i] = (BYTE)(sum_y0 * wy0 + sum_y1 * wy1);

115     }

116 }

View Code

测试代码采用隔一定时间增加一个波源，可以产生动态效果。其中调用了opencv读写和显示图像，相关的头文件和库自己加上即可。

 1 void test_rippling()

 2 {    

 3     Mat mImg = imread("C:/test2.jpg");

 4     imshow("org", mImg);

 5     CRippling rippling;

 6     for(int t = 0; t < 10000; t++)

 7     {

 8         if(t % 20 == 0)

 9         {

10             CWaveSource wavesource(50 + rand() % 800, 50 + rand() % 300);

11             rippling.AddSource(wavesource);

12         }

13 

14         printf("\rtimes: %d", t);

15         Mat mSrc = mImg.clone();

16         Mat mDst = mImg.clone();

17 

18         rippling.Process(mDst.data, mSrc.data, mSrc.cols, mSrc.rows, 3);

19         rippling.Propagate();

20         imshow("pro", mDst);

21         waitKey(1);

22     }

23     waitKey(0);

24 }

View Code

这样基本就完成了，可以实现最开始那张图的效果了。

 

总结 

---

　　上面的分析与实现只是按照原始的产生与传播过程来做的，可以想象，随着波源数的增加，算法的耗时会不断增加，当然在代码注释中也在有的地方说明了可以优化的点。另外，如果我们仅仅是实现这样一个效果，很多波源参数给固定下来，那么可以在算法上进一步推导，从而简化运算。比如，固定波速与波长，让波的周期是4个或2个单位之间，那么应该可以推导出后一时刻位移为前面几个时刻位移的关系，这样就不用每次计算sin函数了。

　　当然上面的推导只考虑了简单情况，特别地，成像一般会近大远小，因此在图像上下方波的扩张速度和质点偏移都是不一样的，对于完整的模型这些都是应该要考虑的因素。

 

 

---