R语言动量交易策略分析调整后的数据

原文链接：http://tecdat.cn/?p=18686

 

用于动量策略中所谓的动量（Momentum），是指某一对象所具有的一种倾向于保持其原有属性或特征的性质，也可以简单理解成一种惰性（Inertia）。股票的动量，简单地说就是涨的还会接着涨，跌的还会接着跌；过去涨得越猛，未来涨的也就越猛；过去跌得越狠，未来也会跌的越狠。

下面，本文将尝试将动量策略应用于调整后的数据（历史价格，股息和拆分数据，以预测公司的未来或获得市场见解）：

#*****************************************************************
# 加载一天结束时的历史数据
#*****************************************************************

# 股票代码
tickers = '
AGG  
DBC  
EEM  
EFA  
'
 


getSymbols.extra(tickers, src = 'yahoo', from = '1970-01-01', env = data, set.symbolnames = T, auto.assign = T)

#*****************************************************************
# 构建另一个不含股利的价格调整后的回测环境


#*****************************************************************

  for(i in data$symbolnames) data.price[[i]] = adjustOHLC(data[[i]], symbol.name=i, adjust='split', use.Adjusted=F)


#*****************************************************************
# 调整价格
#*****************************************************************
for(i in data$symbolnames) data[[i]] = adjustOHLC(data[[i]], use.Adjusted=T)
prep(data, align='keep.all')

我们构建了两个环境：

• 包含拆分和股息调整后的价格
• 仅包含调整后的价格

#*****************************************************************
# 排名60天变化率

#******************************************************************
return = prices / mlag(prices,60) - 1
position.score = iif(return < 0, NA, return)
data$weight[period.ends0,] = ntop(position.score[period.ends1,], 1)



#*****************************************************************
# 60/120天的排名变化率
#******************************************************************
return = prices / mlag(prices,60) - 1 + prices / mlag(prices,120) - 1
position.score = iif(return < 0, NA, return)


  data$weight[period.ends0,] = ntop(position.score[period.ends1, , 1)


#*****************************************************************
# 创建报表
#*****************************************************************
plot(models)

 

 

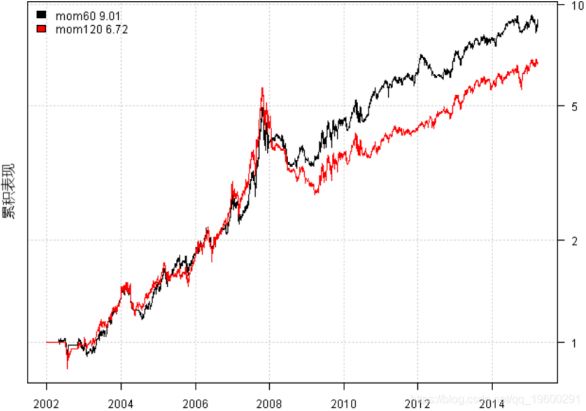
	mom60	mom120
Period	Jan2002 - Mar2015	Jan2002 - Mar2015
Cagr	18.05	15.47
Sharpe	0.89	0.76
DVR	0.85	0.7
R2	0.95	0.92
Volatility	21.26	22.21
MaxDD	-33.49	-51.75
Exposure	94.36	94.36
Win.Percent	63.76	62.42
Avg.Trade	1.69	1.49
Profit.Factor	2.24	2
Num.Trades	149	149

 

models$mom60	weight	entry.date	exit.date	nhold	entry.price	exit.price	return
SPY	100	2013-06-28	2013-07-31	33	155.04	163.06	5.17
XLV	100	2013-07-31	2013-08-30	30	49.88	48.12	-3.53
XLV	100	2013-08-30	2013-09-30	31	48.12	49.66	3.20
FXI	100	2013-09-30	2013-10-31	31	35.92	36.40	1.34
EEM	100	2013-10-31	2013-11-29	29	41.16	41.05	-0.27
XLV	100	2013-11-29	2013-12-31	32	54.24	54.64	0.75
SPY	100	2013-12-31	2014-01-31	31	180.35	173.99	-3.53
XLV	100	2014-01-31	2014-02-28	28	55.16	58.59	6.22
IYR	100	2014-02-28	2014-03-31	31	65.72	65.81	0.14
IYR	100	2014-03-31	2014-04-30	30	65.81	67.81	3.04
EEM	100	2014-04-30	2014-05-30	30	40.42	41.62	2.97
EEM	100	2014-05-30	2014-06-30	31	41.62	42.62	2.40
IYR	100	2014-06-30	2014-07-31	31	70.41	70.33	-0.11
FXI	100	2014-07-31	2014-09-30	61	39.96	37.80	-5.41
UUP	100	2014-09-30	2014-10-31	31	22.87	23.09	0.96
XLV	100	2014-10-31	2014-11-28	28	67.02	69.35	3.48
XLV	100	2014-11-28	2014-12-31	33	69.35	68.38	-1.40
IYR	100	2014-12-31	2015-01-30	30	76.84	81.23	5.71
IYR	100	2015-01-30	2015-02-27	28	81.23	79.12	-2.60
FXI	100	2015-02-27	2015-03-30	31	43.76	44.74	2.24

接下来，我们考虑以下3种设置：

• “已调整”-拆分和股息调整后的价格数据。信号和损益仅从调整后的数据时间序列中得出。
• “实际”-仅使用拆分后的调整数据，尚未对股息进行调整。信号和损益仅从唯一的拆分调整后的数据时间序列中得出。
• “混合”-使用“实际”时间序列生成信号，使用“调整”时间序列进行损益计算。

#*****************************************************************
# 辅助函数
#******************************************************************


    
  return = prices / mlag(prices,60) - 1
  position.score = iif(return < 0, NA, return)


  return = prices / mlag(prices,60) - 1 + prices / mlag(prices,120) - 1
  position.score = iif(return < 0, NA, return)


  models[[paste0('mom120',name)]] =run(data, clean.signal=F, commission = commission, trade.summary=T, silent=T)
  
  models

#*****************************************************************
# 安装
#******************************************************************

all.models = c(all.models, strategy(prices.adj, data, 'Adjusted'))


#*****************************************************************
# 创建报表
#*****************************************************************

plot(models

 

print(plotbt.strateg(models, make.plot=F,

 

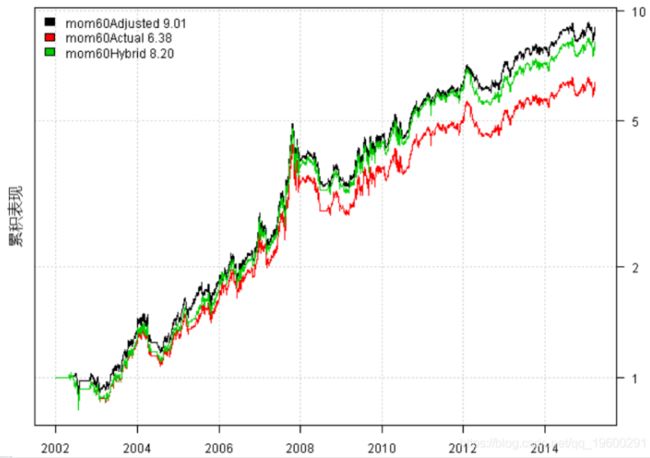
	mom60Adjusted	mom60Actual	mom60Hybrid
Period	Jan2002 - Mar2015	Jan2002 - Mar2015	Jan2002 - Mar2015
Cagr	18.05	15.02	17.22
Sharpe	0.89	0.76	0.85
DVR	0.85	0.73	0.82
R2	0.95	0.96	0.96
Volatility	21.26	21.33	21.33
MaxDD	-33.49	-35.99	-33.74
Exposure	94.36	92.44	92.44
Win.Percent	63.76	62.33	63.01
Avg.Trade	1.69	1.49	1.67
Profit.Factor	2.24	1.98	2.15
Num.Trades	149	146	146

plotbt(models, plotX = T, log = 'y'

 

print(plotstrategy)

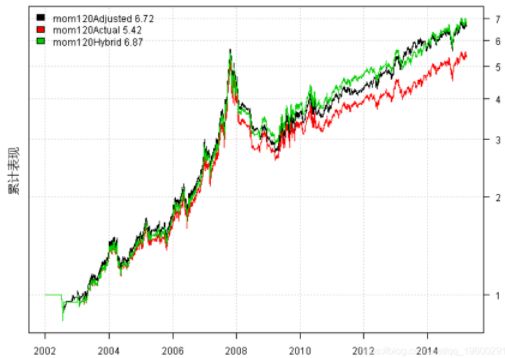
	mom120Adjusted	mom120Actual	mom120Hybrid
Period	Jan2002 - Mar2015	Jan2002 - Mar2015	Jan2002 - Mar2015
Cagr	15.47	13.61	15.66
Sharpe	0.76	0.69	0.77
DVR	0.7	0.64	0.73
R2	0.92	0.92	0.94
Volatility	22.21	22.08	22.07
MaxDD	-51.75	-49.93	-47.15
Exposure	94.36	92.47	92.47
Win.Percent	62.42	60.96	61.64
Avg.Trade	1.49	1.37	1.54
Profit.Factor	2	1.9	2.02
Num.Trades	149	146	146

经调整后的数据表现优于实际数据和混合数据。

---

最受欢迎的见解

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用

2.R语言GARCH-DCC模型和DCC（MVT）建模估计

3.R语言实现 Copula 算法建模依赖性案例分析报告

4.R语言COPULAS和金融时间序列数据VaR分析

5.R语言多元COPULA GARCH 模型时间序列预测

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model

9.matlab使用Copula仿真优化市场风险