多元统计分析及R语言建模（第五版）——第2章 多元数据的数字表达课后习题
第2章 多元数据的数字表达
文章会用到的数据请在这个网址下下载多元统计分析及R语言建模（第五版）数据
练习题
1）对下面的相关系数矩阵，试用R语言求其逆矩阵，特征根和特征向量…，要求写出R语言计算函数
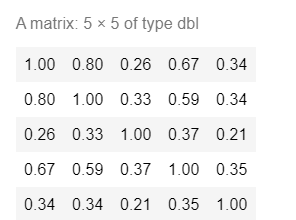
R=
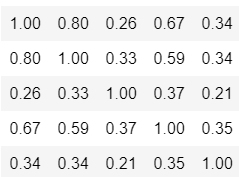
要求写出R语言计算函数。
A = matrix(c(1.00,0.80,0.26,0.67,0.34,0.80,1.00,0.33,0.59,0.34,0.26,0.33,1.00,0.37,0.21,
0.67,0.59,0.37,1.00,0.35,0.34,0.34,0.21,0.35,1.00),nrow = 5,ncol = 5) #生成矩阵A
A
#矩阵求逆运用函数solve()
solve(A) #求A矩阵的逆矩阵
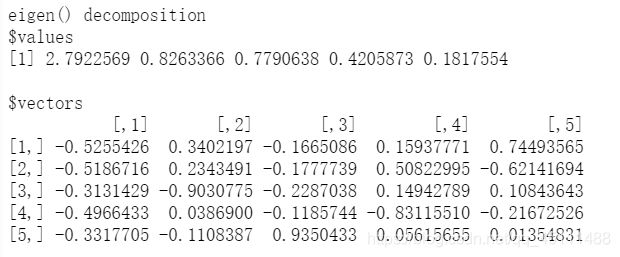
#求矩阵的特征值和特征向量运用函数eigen()函数
A.e = eigen(A,symmetric = T) #求A矩阵的特征值
A.e
A.e $ vectors%*%diag(A.e $ values)%*%t(A.e $ vectors) #求A矩阵的特征向量
2）某厂对50个计件工人某月份工资进行登记，获得以下原始资料（单位：元）…试按组距为300编制频数表，计算频数、频率和累积频率，并绘制直方图。
(1)写出R语言统计
library(openxlsx)
d2.2 = read.xlsx('mvexer5.xlsx',sheet ='E2.2')
head(d2.2)
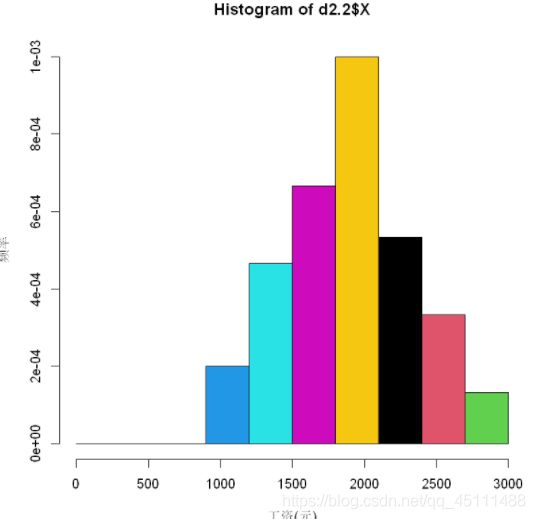
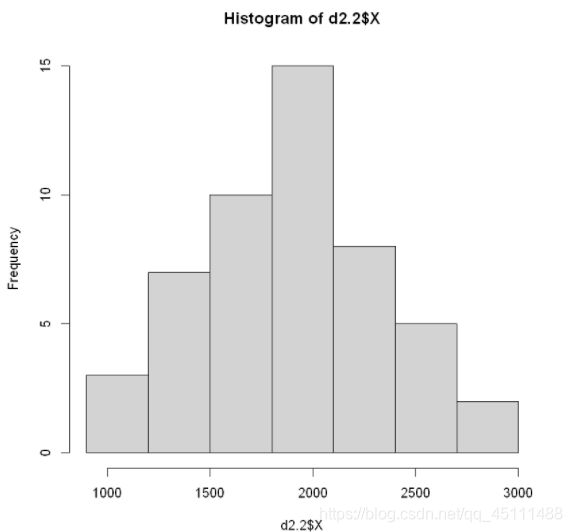
hist(d2.2 $ X,breaks = seq(0,3000,by = 300),col = 1:7,xlab = "工资(元)",ylab = "频数") #绘制频数直方图
hist(d2.2 $ X ,m,freq = F,col = 1:7,xlab = "工资(元)",ylab = "频率") #绘制频率直方图
Cumsum <- cumsum(d2.2 $ X)
M <- seq(0,96000,by = 3000)
hist(Cumsum,M,freq = F,col = 1:12,las = 3,xlab = "工资(元)",ylab = "累积频率") #绘制累积频率直方图
（2）用R语言进行基本统计分析
min(d2.2)
max(d2.2)
可以得到某月份最低工资为1000，最高工资为2980
H1 = hist(d2.2 $ X,breaks = seq(900,3000,300)) #以组距为300画直方图
编制频数表，列出频数、频率、和累积频率
names(H1)
data.frame('组中距' = H1 $ mids,'频数' = H1 $ counts,'频率' = H1 $ density*300,'累积频率' = cumsum(H1 $ density*300))
（3）用R语言作正态概率图并分析之
qqnorm(d2.2 $ X)
qqline(d2.2 $ X)
由正态概率图可以看出数据点基本是一条直线，因此数据可以近似看作正态分布。
3)以下是一份关学生是否抽烟与每天学习时间长短关系的调查数据，试用R语言对其进行基本统计分析。
d2.3 = read.xlsx('mvexer5.xlsx',sheet = 'E2.3')
d2.3
对数据进行简单的统计分析
dim(d2.3 )
names(d2.3 )
str(d2.3)
summary(d2.3 )
可以看到抽取的学生中4位不抽烟，6位抽烟，每天学习时间小于5小时的有3位，5-10小时的有4位，超过10小时的有3位，抽烟情况和学习时间分别的分布比较均匀。
4)试编制进行计量数据频数表分析的R语言函数
ch = function(X){
H = hist(X)
n = H $ breaks[2] - H $ breaks[1]
c = data.frame('组中值' = H $ mids,'频数' = H $ counts,'频率' = H $ density*n,
'累积频率' = cumsum(H $ density*n))
c
}
ch(d2.2 $ X )
