1.2 状态空间描述

输入输出描述

我们建立了一个描述线性系统零状态响应的数学方程。假设初始状态为零，输出只由输入决定。考虑一个SISO线性系统。

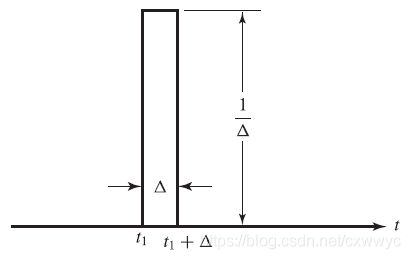
如图所示的单位脉冲信号表达式为$u(t)={\delta }_{\Delta }(t-t_1)$。

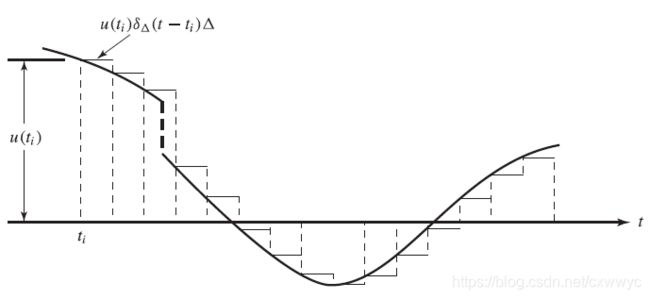
然后，每个输入$u(t)$都可以用如图所示的一系列脉冲来近似。因此，输入$u(t)$可以近似表示为
$$u\left(t\right)\approx \sum _{i}u\left(t_i\right){\delta }_{\Delta }\left(t-t_i\right)\Delta$$
设$g_{\Delta }(t,t_i)$为施加于$t$时刻的脉冲$u(t)={\delta }_{\Delta }(t-t_i)$在$t_i$的输出。于是

$${\delta }_{\Delta }\left(t-t_i\right)\to g_{\Delta }\left(t-t_i\right)$$
$${\delta }_{\Delta }\left(t-t_i\right)u\left(t_i\right)\Delta \to g_{\Delta }\left(t-t_i\right)u\left(t_i\right)\Delta （齐次性）$$
$$\sum _i{\delta }_{\Delta }\left(t-t_i\right)u\left(t_i\right)\Delta \to \sum _i{g}_{\Delta }\left(t-t_i\right)u\left(t_i\right)\Delta （可加性）$$
因此输入$u(t)$激发的输出$y(t)$可以近似为
$$y\left(t\right)\approx \sum _{i}u\left(t_i\right)g_{\Delta }\left(t-t_i\right)\Delta$$
现在，令$\Delta$接近于零，则脉冲${\delta }_{\Delta }(t-t_i)$变为理想脉冲$t_i$，表示为$\delta (t-t_i)$，相应的输出将表示为$g(t,t_i)$。当$\Delta$接近于零时，上面公式中约等号中的变成等号，求和变成积分，离散的时间变成连续时间，可以用$\tau$代替，并且$\Delta$可以写为$d\tau$。因此
$$y\left(t\right)={\int }_{-\infty }^{\infty }g\left(t,\tau \right)u\left(\tau \right)\text{d}\tau$$
注意，$g(t,\tau )$是两变量的函数。第二个变量表示施加脉冲输入的时间；第一个变量表示产生输出的时间。因为$g(t,\tau )$是由脉冲激励的响应，所以它被称为脉冲响应。
如果系统是因果系统，则在输入之前不会有输出。这样就有
$$\text{系统是因果的}⟺g\left(t,\tau \right)=0,t<\tau$$
如果系统在$t_0$处的初始状态为$0$，则称该系统在$t_0$处松弛。在这种情况下，$t\ge t_0$的输出$y(t)$只由$t\ge t_0$的输入$u(t)$激励。因此，可以用$t_0$代替积分下限。如果系统是因果的，则对于$t<\tau ,g(t,\tau )=0$。因此，积分上限可以用$t$代替。总而言之，每个在$t_0$处松弛的因果线性系统都可以用下面的公式来描述
$$y\left(t\right)={\int }_{t_0}^{t}g\left(t,\tau \right)u\left(\tau \right)\text{d}\tau$$
如果线性系统有$p$个输入和$q$个输出，则方程可以扩展到
$$\mathbf{y}\left(t\right)={\int }_{t_0}^t\mathbf{G}\left(t,\tau \right)\mathbf{u}\left(\tau \right)\text{d}\tau$$
其中
$$\mathbf{G}\left(t,\tau \right)=\left[\begin{array}{cccc}{g}_{11}\left(t,\tau \right)& g_{12}\left(t,\tau \right)& \cdots & g_{1p}\left(t,\tau \right)\\ g_{21}\left(t,\tau \right)& g_{22}\left(t,\tau \right)& \cdots & g_{2p}\left(t,\tau \right)\\ ⋮& ⋮& \ddots & ⋮\\ g_{q1}\left(t,\tau \right)& g_{q2}\left(t,\tau \right)& \cdots & g_{qp}\left(t,\tau \right)\end{array}\right]$$
而$g_{ij}(t,\tau )$是在时间$t$处的第$i$个输出端处的响应，这是由于在时间$t$处施加在第$j$个输入端处的脉冲，在其他输入端处的输入为零。也就是说，$g_{ij}(t,\tau )$是第$j$个输入端和第$i$个输出端之间的脉冲响应。因此，$\mathbf{G}$称为系统的脉冲响应矩阵。再次强调，这种情况下系统是线性的，在$t_0$处是松弛的，并且是因果的。

状态空间描述

每个线性集总参数系统都可以用以下形式的一组方程来描述
$$\begin{array}{c}\dot{\mathbf{x}}\left(t\right)=\mathbf{A}\left(t\right)\mathbf{x}\left(t\right)+\mathbf{B}\left(t\right)\mathbf{u}\left(t\right)\\ \mathbf{y}\left(t\right)=\mathbf{C}\left(t\right)\mathbf{x}\left(t\right)+\mathbf{D}\left(t\right)\mathbf{u}\left(t\right)\end{array}$$
对于$p$输入$q$输出系统，$\mathbf{u}$是$p\times 1$矢量，$\mathbf{y}$是$q\times 1$矢量。如果系统有$n$个状态变量，则$\mathbf{x}$是一个$n\times 1$的向量。为了使方程两侧矩阵兼容，$\mathbf{A}$、$\mathbf{B}$、$\mathbf{C}$和$\mathbf{D}$必须是$n\times n$、$n\times p$、$q\times n$和$q\times p$矩阵。这四个矩阵都是时间$t$的函数。这两个方程描述的是$n$维状态空间方程，或者简称为状态方程。对于分布式系统，维数为无穷大，不使用这两个方程描述。