离散数学精简笔记 ——《图论》
一.图的基本概念
图(graph) G:G=(V,E,γ)由顶点(vertex)集V和边(edge)集E,γ组成
无特殊说明n表示图G的定点数,m表示图G的边数,一边数为m的n阶图可简化为(n,m)-图
顶点(vertex) V :或结点 ,|V|为G的阶,X阶图指的顶点个数
边(edge) E :平常写作{e1,e2……}
函数(γ) :为E到V的一个函数,有γ(e)={v1,v2},表示v1,v2顶点间的关系,γ通常表示线。即顶点间使用线(γ)来联系
邻接:若两个顶点之间有边存在,则称这两个顶点邻接
关联:若边的无序对(有序对)包含该节点,则称该顶点与这条边相关联。
度(degree):节点的度指的是与节点v邻接的节点数。记作:deg(v)。(自环在计度时为2)
孤立点:度为0的节点。
端节点:度为1的节点(也叫做:叶子)
简单图:任意两个节点之间最多只能有一条边存在。
多重图:允许指定的两个节点之间存在两条及两条以上的边。
正则图:图中所有的节点有相同的度数。(r-正则图表示所有节点的度都是r)
无向图:边没有方向性。
有向图:边具有方向性。
完全图:完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
加权图:是一种赋予了边值的图,这些值称为权重或者成本。
入度:以顶点v为终点的边的数目,称为v的入度。
出度:以顶点v为始点的边的数目,称为v的出度。
度(有向):有向图中的度为出度和入度之和。
最大度:所有节点的最大度数。
最小度:所有节点的最小度数。
欧拉定理(握手定理): 图论基本定理,在任何图中,所有顶点度数的和等于边数的两倍。
推论:在任何图中,节点度的总和是一个非负偶数。
图的同构:
存在对图G1,G2中,V(顶点)与E(边)的双射。下面两图具有相同的性质,可看作左上红点拉入中间得到右图,各个颜色相同的点性质相同
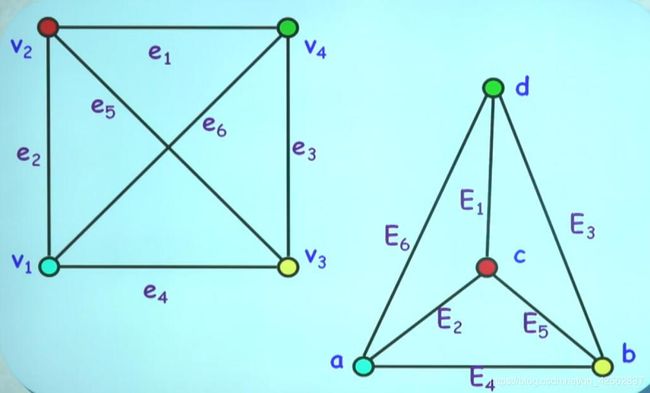
子图:指节点集和边集分别是某一图的节点集的子集和边集的子集的图(原图删去一些边和节点)
真子图:这个节点子集或边子集是真子集(不允许什么都不删)
生成子图或称支撑子图:图G的每一个节点也是它的子图H的节点(保留全部节点,只删边)
导出子图:
(1)顶点导出子图:若V1⊆V(G),则以V1为顶点集,以两个顶点均在V1中的边集组成的图,称为图G的顶点导出子图,记为G(V1)。
(2)边的导出子图:若E1⊆E(G),则以E1为边集,以E1中所有边的顶点为顶点集组成的图,称为图G的边的导出子图,记为G(E1)。
补图:图G的补图,通俗的来讲就是完全图Kn去除G的边集后得到的图Kn-G。
连通性
道路:两点之间可达的路径
回路:能回到起点的道路
简单路径(初级道路或初级回路):其上的所有顶点都是互异的,但第一个顶点和最后一个顶点可能相同
定理:若简单图G中的每个顶点的度数都大于1,则G中存在回路
连通图:
(1)设图为无向图,如果图中任意两相异点之间都存在道路,则称为连通图
(2)设图为有向图,如果图中任意两相顶点之间都是可达的,则称为强连通。任意两顶点u和v,只有u到v或v到u则称为单向连通
桥(割边):如果删除一边,使得图不再连通,则称该边为桥或割边
图的矩阵表示
- A中第i行元素之和为顶点vi的出度
- A中第i列元素之和为顶点vi的入度
- A是对称矩阵
- A中的第i行元素之和等于第i列元素之和,为顶点vi的度数


