CatBoost论文笔记
CatBoost: gradient boosting with categorical features support(有类别属性支持的梯度提升)
→原文链接
Abstract
- 我们提出的Catboost算法很6,开源,处理类别属性比现有的梯度提升都厉害(用的一些主流的开源数据集)
CatBoost, a new open-sourced gradient boosting library that successfully handles categorical features and outperforms existing publicly available implementations of gradient boosting in terms of quality on a set of popular publicly available datasets.
- 我们的算法速度很快,我们有算法的GPU实现以及CPU实现的评分算法,比现在其他的梯度提升算法都快,嗯,快还不大。
The library has a GPU implementation of learning algorithm and a CPU implementation of scoring algorithm, which are significantly faster than other gradient boosting libraries on ensembles of similar sizes.
Introduction
- 介绍部分前两段先夸了现有的梯度提升算法很厉害,并指出现在的此类算法都用的是决策树作为基学习器,顺便也夸了一下决策树也肯厉害,但是指出了决策树存在的问题:类别特征不能直接进入训练,需要预处理。
Gradient boosting is a powerful machine-learning technique that achieves state-of-the-art results in a variety of practical tasks. For a number of years, it has remained the primary method for learning problems with heterogeneous features(异质特征), noisy data, and complex dependencies: web search, recommendation systems, weather forecasting, and many others(举例说明梯度提升可以处理的问题). It is backed by strong theoretical results that explain how strong predictors can be built by iterative combining weaker models (base predictors) via a greedy procedure that corresponds to gradient descent in a function space.
Most popular implementations of gradient boosting use decision trees as base predictors. It is convenient to use decision trees for numerical features, but, in practice, many datasets include categorical features, which are also important for prediction. Categorical feature is a feature having a discrete set of values that are not necessary comparable with each other (e.g., user ID or name of a city). The most commonly used practice for dealing with categorical features in gradient boosting is converting them to numbers before training.(指出在梯度提升方法中对类别特征的方法大多是在训练之前转化这些特征)
- 三四段指出了catboost的不同之处:1.在训练期间处理类别特征。2.提出了一个新的选择树结构的方式,可以减少过拟合。然后又夸了一遍自己的算法比现有的xgb,lgb,h2o2啥的都优秀,叫Catboost的原因是categorical boosting
In this paper we present a new gradient boosting algorithm that successfully handles categorical features and takes advantage of dealing with them during training(在训练期间处理类别特征) as opposed to preprocessing time. Another advantage of the algorithm is that it uses a new schema for calculating leaf values when selecting the tree structure(提出了一个新的选择树结构的方式), which helps to reduce overfitting.
As a result, the new algorithm outperforms the existing state-of-the-art implementations of gradient boosted decision trees (GBDTs) XGBoost [4], LightGBM1 and H2O2 , on a diverse set of popular tasks (Sec. 6). The algorithm is called CatBoost (for “categorical boosting”) and is released in open source.3
Categorical features
Categorical features这一部分主要讲解了如何把离散特征的处理与标签(label值,y值)关联起来。
这个公式加上了超参数,变成了![\frac{\sum_{j=1}^{p-1}[x_{\sigma_{j,k}}=x_{\sigma_{p,k}}]Y_{\sigma_j}+a\cdot P}{\sum_{j=1}^{p-1}[x_{\sigma_{j,k}}=x_{\sigma_{p,k}}]+a}](http://img.e-com-net.com/image/info8/0d1828ed08e0436b825b4fa3b17e9335.gif) (计算相同类别值的样本的平均标签值,加上a和P防止过拟合)
(计算相同类别值的样本的平均标签值,加上a和P防止过拟合)
- 第一段先说了类别特征不需要互相比较,因此不能直接用于决策树,一个通用的处理方式是在训练之前将类别特征转化为数字类型,每个样本的每个类别都对应一个或几个数值。
- 第二段指出了最常用的类别特征转化方法:one-hot encoding,并表示catboost采用了在训练之中使用one-hot编码,这样可以更加高效。
Categorical features have a discrete set of values called categories which are not necessary comparable with each other; thus, such features cannot be used in binary decision trees directly. A common practice for dealing with categorical features is converting them to numbers at the preprocessing time, i.e., each category for each example is substituted with one or several numerical values.
The most widely used technique which is usually applied to low-cardinality categorical features is one-hot encoding: the original feature is removed and a new binary variable is added for each category [14]. One-hot encoding can be done during the preprocessing phase or during training(onehot编码在训练前和训练中处理都可以), the latter can be implemented more efficiently in terms of training time and is implemented in CatBoost(指出Catboost使用的是后一种,在训练中处理的,因为这样可以更高效).
- 另一种处理类别特征的方式通过样本的标签来计算一些统计信息,最简单的是用整个训练集上的标签平均值替换该类别,但是这样显然容易过拟合(文中举了一个例子:假如整个训练集中只有这一个样本的情况),解决办法是分成训练集和验证集
Another way to deal with categorical features is to compute some statistics using the label values of the examples. Namely, assume that we are given a dataset of observations
, where
is a vector of m features, some numerical, some categorical, and
is a label value. The simplest way is to substitute the category with the average label value on the whole train dataset.(用整个训练集上的标签平均值替换该类别) So,
is substituted with
, where [·] denotes Iverson brackets(艾弗森括号:括号内的条件满足则为1,不满足则为0), i.e.,
equals 1 if
and 0 otherwise. This procedure, obviously, leads to overfitting. For example, if there is a single example from the category
in the whole dataset then the new numeric feature value will be equal to the label value on this example.(过拟合反例) A straightforward way to overcome the problem is to partition the dataset into two parts and use one part only to calculate the statistics and the second part to perform training. This reduces overfitting but it also reduces the amount of data used to train the model and to calculate the statistics.
- CatBoost使用了一种更有效的可以减少过拟合的策略,并可以使用整个数据集进行训练。计算样本标签均值的方式。
CatBoost uses a more efficient strategy which reduces overfitting and allows to use the whole dataset for training. Namely, we perform a random permutation of the dataset and for each example we compute average label value for the example with the same category value placed before the given one in the permutation.(计算相同类别值的样本的平均标签值) Let
be the permutation(组合方式), then
is substituted with
,
where we also add a prior value P and a parameter a > 0, which is the weight of the prior.(加上了先验值P和先验值的权重参数a) Adding prior is a common practice and it helps to reduce the noise obtained from low-frequency categories.(加上P的目的是减少从低频类别特征得来的噪声) For regression tasks standard technique for calculating prior is to take the average label value in the dataset. For binary classification task a prior is usually an a priori probability of encountering a positive class(计算P的方式:回归任务取数据集中标签平均值;二分类任务取遇到正例的先验概率). It is also efficient to use several permutations. However, one can see that a straightforward usage of statistics computed for several permutations would lead to overfitting. As we discuss in the next section, CatBoost uses a novel schema for calculating leaf values which allows to use several permutations without this problem.(引出catboost使用的新的计算叶值的模型)
Feature combinations
- 特征结合方式,
Note that any combination of several categorical features could be considered as a new one.(任意几个类别特征的组合都可以被看做一个新的特征) For example,assume that the task is music recommendation and we have two categorical features: user ID and musical genre. Some user prefers, say, rock music. When we convert user ID and musical genre to numerical features according to (1), we loose this information. (当我们用公式1转化userID和musical genre时,我们释放了这一信息)A combination of two features solves this problem and gives a new powerful feature.(两个特征组合成的特征变成了一个新的强特) However, the number of combinations grows exponentially with the number of categorical features in dataset and it is not possible to consider all of them in the algorithm. (然而组合特征的数量会随着特征数量变多而指数级增长,所以不可能在算法中把所有的特征都用上)When constructing a new split for the current tree, CatBoost considers combinations in a greedy way.(当我们分割当前树的时候,catboost是以贪心的方式进行) No combinations are considered for the first split in the tree.(树的第一次分割时,不考虑组合特征) For the next splits CatBoost combines all combinations and categorical features present in current tree with all categorical features in dataset. (在下一次分割时catboost将所有当前树种的类别特征和所有数据集中的类别特征组合)Combination values are converted to numbers on the fly. (组合值在fly上转化为数值特征)CatBoost also generates combinations of numerical and categorical features in the following way(catboost也以一下方式生成数字和类别特征组合): all the splits selected in the tree are considered as categorical with two values and used in combinations in the same way as categorical ones. (树中选择的所有拆分都被视为二分类,在组合特征中也用相同的方式。)
Important implementation details
- 用类别在数据集出现的次数替换类别特征
Another way of substituting category with a number is calculating number of appearances of this category in the dataset.(另一种用数字替换类别的方式是用这个类别在数据集出现的次数替换) This is a simple but powerful technique and it is implemented in CatBoost. (这种方式在catboost中也用到了)This type of statistic is also calculated for feature combinations.(这种类型的统计也针对特征组合进行计算) In order to fit the optimal prior at each step of CatBoost algorithm,(为了在CatBoost每步中确定最佳先验) we consider several priors and construct a feature for each of them(我们考虑了几个先验,并为每个先验构造了一个特征), which is more efficient in terms of quality than standard techniques mentioned above.
Fighting Gradient Bias
这部分要解决一个问题:噪声点问题。
- 第一段提出了导致过拟合的噪声点问题,
CatBoost, as well as all standard gradient boosting implementations, builds each new tree to approximate the gradients of the current model(catboost和其他梯度提升模型一样,建立新的树去拟合当前模型的梯度). However, all classical boosting algorithms suffer from overfitting caused by the problem of biased pointwise gradient estimates.(然而,所有经典的梯度提升算法都面临着由于biased pointwise梯度估计引起的过拟合问题,这个biased pointwise说白了就是噪声点引起的过拟合问题) Gradients used at each step are estimated using the same data points the current model was built on.(在每步中使用的梯度都是使用当前模型基于一个数据点估计的) This leads to a shift of the distribution of estimated gradients in any domain of feature space in comparison with the true distribution of gradients in this domain(这导致在特征空间任意区域的梯度估计的分布与空间上真实梯度的分布相比发生了变化), which leads to overfitting(导致过拟合). The idea of biased gradients was discussed in previous literature [1] [9]. We have provided a formal analysis of this problem in the paper [5]. The paper also contains modifications of classical gradient boosting algorithm that try to solve this problem.(还对经典的梯度提升算法进行改进) CatBoost implements one of those modifications, briefly described below. (catboost实现了其中一种)
-
阐述gbdt模型建造树的过程和catboost对树模型的改进,第一阶段确定树结构时提出了新方法,第二阶段向叶子结点填值的时候还是采用传统方式(梯度或牛顿过程)
In many GBDTs (e.g., XGBoost, LightGBM) building next tree comprises two steps: choosing the tree structure and setting values in leafs after the tree structure is fixed. (其他GBDT模型新建一棵树包含两步:1,确定树结构2,向叶子结点填值)To choose the best tree structure, the algorithm enumerates through different splits, builds trees with these splits, sets values in the obtained leafs, scores the trees and selects the best split.(为了选择最佳的树结构,gbdt类的算法通过不同的拆分进行枚举,用这些拆分构建树,在获得的叶子节点中填值,对树进行评分并选择最佳的拆分。) Leaf values in both phases are calculated as approximations for gradients [8] or for Newton steps.(两步的叶值计算为梯度或Newton steps的近似值。) In CatBoost the second phase is performed using traditional GBDT scheme and for the first phase we use the modified version. (在CatBoost中,第二步使用传统的GBDT方法进行,第一步使用改进后的方法。)
-
catboost对建树过程的改进:这段说的比较难懂,我理解的意思是:训练第i轮第k次的时候,不使用第k次的训练数据
 ,那么如何做到不用这个
,那么如何做到不用这个 还能保证能训练的呢?文中说用一个分离的模型
还能保证能训练的呢?文中说用一个分离的模型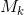 ,这个模型只用来估计
,这个模型只用来估计 上的梯度。说到这还是有些不明白是怎么做到的,看一下伪代码:
上的梯度。说到这还是有些不明白是怎么做到的,看一下伪代码:
- 最内层for循环:对于前
 条数据,依次计算
条数据,依次计算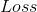 的梯度
的梯度 ,然后将前
,然后将前 条数据和其对应的
条数据和其对应的 个梯度值
个梯度值 传入函数LearnOneTree得到残差树
传入函数LearnOneTree得到残差树
- 第二层for循环:更新
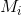 ,向上一个
,向上一个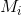 添加
添加 得到新的
得到新的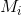
- 最外层循环:最后生成n个
 ,
,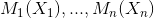
意思就是,利用所有训练集(除第i条)建立模型![]() ,然后使用第1条到第i-1条数据来建一个修正树
,然后使用第1条到第i-1条数据来建一个修正树![]() ,累加到原来模型
,累加到原来模型![]() 上
上
According to intuition obtained from our empirical results and our theoretical analysis in [5], it is highly desirable to use unbiased estimates of the gradient step. (根据我们的经验和分析,最好使用梯度阶跃的无偏估计)Let
be the model constructed after building first i trees,
be the gradient value on k-th training sample after building i trees.(
是前
颗树建成后的模型,
是建立 i 颗树后第k次训练样本的梯度值)To make the gradient
unbiased w.r.t. the model
, we need to have
trained without the observation
. (为了使梯度值关于模型无偏,我们需要训练
时不观测
)Since we need unbiased gradients for all training examples, no observations may be used for training
, which at first glance makes the training process impossible. (因为我们需要所有训练样本的无偏梯度,然而在训练
时不能观测,这看起来不太可能)We consider the following trick to deal with this problem: for each example
, we train a separate model
that is never updated using a gradient estimate for this example.(如何解决:训练一个分离的模型
,这个模型从来不用梯度估计进行更新) With
, we estimate the gradient on
and use this estimate to score the resulting tree.(我们用
来估计
上的梯度,然后用这个估计对树进行评分) Let us present the pseudo-code that explains how this trick can be performed.(介绍这部分的伪代码) Let Loss
be the optimizing loss function, where y is the label value and a is the formula value. (设损失
是优化损失函数,y是标签值,a是公式值)
Note that
is trained without using the example
. CatBoost implementation uses the following relaxation of this idea: all
share the same tree structures.(
是在不使用样本
训练的,catboost实现:所有的
共用相同的树结构)
In CatBoost we generate
random permutations of our training dataset. (在catboost中我们对数据集进行了
次随机排序)We use several permutations to enhance the robustness of the algorithm: we sample a random permutation and obtain gradients on its basis. (我们使用了几种排序来增强算法的鲁棒性:对一个随机排序进行抽样然后通过他获得梯度)These are the same permutations as ones used for calculating statistics for categorical features. (这些和计算类别特征的统计信息用的是相同的排序)We use different permutations for training distinct models, thus using several permutations does not lead to overfitting. (我们使用不同的排序来训练不同的模型,因此使用几个排序不会导致过拟合。)For each permutation
, we train
different models
, as shown above. (对每个排序
,训练n个不同的模型
)That means that for building one tree we need to store and recalculate
approximations for each permutation σ: (这意味着对于每一棵树的构建,我们需要存储和重新计算
次每个排序的近似值σ)for each model
, we have to update
.(对于每个模型
,我们需要更新
) Thus, the resulting complexity of this operation is
.(所以最后这个操作的复杂度是
) In our practical implementation, we use one important trick which reduces the complexity of one tree construction to
(在实现中用了一个技巧将构造一棵树的复杂度降低到了
): for each permutation, instead of storing and updating
values
, we maintain values
, where
is the approximation for the sample
based on the first
samples.(对于每个排序,保留M_{i}^{'}(X_j),i=1,...,[log_2(n)],j<2^{i+1}的值,而不是储存并更新
个
的值,其中
是基于前
个样本的样本
的近似值) Then, the number of predictions
is not larger than
. The gradient on the example
used for choosing a tree structure is estimated on the basis of the approximation
, where
.(根据近似值
估计用于选择树结构的样本
的梯度)
Fast scorer
Fast training on GPU
