最大公约数问题
[The Euclidean algorithm] is the granddaddy of all algorithm that has survived to the present day. -- Donald Knuth |
解法一 Euclidean Algorithm 递归实现
欧几里得算法(Euclidean Algorithm)(Euclid‘s 算法)就是通常所说的求最大公因数的辗转相除法。算法描述如下：
- 如果 a 除以 b 能整除，则最大公约数是 b；
- 否则，最大公约数等于 b 和 a % b的公约数。
可以写为 [gcd(a, b) = gcd(b, a mod b)]
代码实现如下：
#include <stdio.h>
int Euclidean(int parA, int parB)
{
if (parB == 0) {
return parA;
} else {
return Euclidean(parB, parA % parB);
}
}
int
main(void)
{
int intA, intB;
printf("Enter two number to calculate its GCD:\n");
scanf("%d %d", &intA, &intB);
printf("The GCD of %d and %d is %d\n", intA, intB, Euclidean(intA, intB));
return 0;
}
#include <stdio.h>
int Euclidean(int parA, int parB)
{
return (!parB)?parA : Euclidean(parB, parA % parB);
}
int
main(void)
{
int intA, intB;
printf("Enter two number to calculate its GCD:\n");
scanf("%d %d", &intA, &intB);
printf("The GCD of %d and %d is %d\n", intA, intB, Euclidean(intA, intB));
return 0;
}
解法二 Euclidean Algorithm 循环实现
递归和循环是等价的，下面使用循环的方式实现 Euclid's 算法。
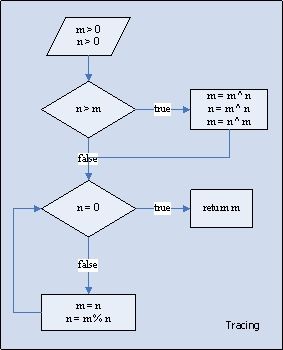
代码如下：
/*
求解正整数的 GCD
*/
#include <stdio.h>
int
EuclideanLoop(int parA, int parB)
{
int tmp = 0;
while (1) {
if (parB == 0) {
return parA;
}
if (parA < parB) {
parA = parA ^ parB;
parB = parA ^ parB;
parA = parB ^ parA;
}
tmp = parA;
parA = parB;
parB = tmp % parB;
}
}
int
main(void)
{
int intA, intB;
printf("Enter two numbers to calculate its GCD \n");
scanf("%d %d", &intA, &intB);
printf("The GCD of %d and %d is %d\n", intA, intB, EuclideanLoop(intA, intB));
return 0;
}
/*
求解正整数的 GCD
*/
#include <stdio.h>
int
EuclideanLoop(int parA, int parB)
{
int tmp = 0;
if (parA < parB) {
parA = parA ^ parB;
parB = parA ^ parB;
parA = parB ^ parA;
}
while (1) {
if (parB == 0) {
return parA;
}
tmp = parA % parB;
parA = parB;
parB = tmp;
}
}
int
main(void)
{
int intA, intB;
printf("Enter two numbers to calculate its GCD \n");
scanf("%d %d", &intA, &intB);
printf("The GCD of %d and %d is %d\n", intA, intB, EuclideanLoop(intA, intB));
return 0;
}
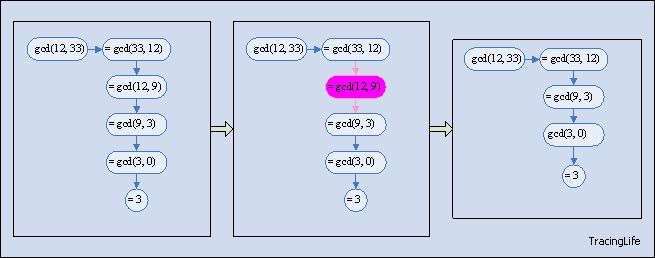
改进后的算法，简化了求解步骤。因为 Euclid 算法中，对于数 m 和 n 的取值都进过了取模运算，所以可以简化求解。如下图：
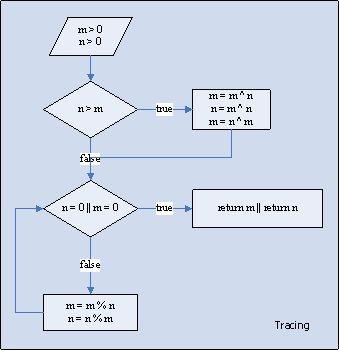其改进的效果如下：
代码实现如下：
/*
求解正整数的 GCD 。
改进上面的算法，使其用更少的步骤实现 Euclid 算法。
*/
#include <stdio.h>
int
EuclideanLoop(int parA, int parB)
{
if (!parA || !parB) {
return 0;
}
if (parA < parB) {
parA = parA ^ parB;
parB = parA ^ parB;
parA = parB ^ parA;
}
while(1) {
if (!(parA = parA % parB)) return parB;
if (!(parB = parB % parA)) return parA;
}
}
int
main(void)
{
int intA, intB;
printf("Enter the two numbers to calculate its GCD\n");
scanf("%d %d", &intA, &intB);
printf("The GCD of number %d and %d is %d\n", intA, intB, EuclideanLoop(intA, intB));
return 0;
}
上面的程序都只解决求解正整数 GCD 的问题，这也是数学上规定的。而对于存在负数的情况则要在求解之前规定成立的条件，一般情况下，算绝对值的最大公约数，而至于 0 ，最大公约数没有意义。
下面的程序给出了求解任意整数最大公约数的方法，规定求解负数绝对值的 GCD。
代码如下：
/*
求解任意整数的 GCD
*/
#include <stdio.h>
int
Euclidean(int parA, int parB)
{
if (!parA || !parB) {
return 0;
}
if (parA < 0) {
return Euclidean(-parA, parB);
}
if (parB < 0) {
return Euclidean(parA, -parB);
}
if (parA < parB) {
return Euclidean(parB, parA);
}
if (parA % parB) {
return Euclidean(parB, parA % parB);
} else {
// 算法求解到最后的形式为 gcd(m, n) = gcd(p, 0)
return parB;
}
}
int
main(void)
{
int intA, intB;
puts("Welcome to the Greatest Common Divisor Program\n\n"
"Enter the first number: ");
scanf("%d", &intA);
puts("Enter the second number: ");
scanf("%d", &intB);
printf("gcd(%d, %d) = %d\n", intA, intB, Euclidean(intA, intB));
return 0;
}
最大公因数，又称最大公约数。是指 [n(≧2)个自然数 a1, a2, ..., an] 的最大公因数。通常有两种表示方式 ● 它们的所有公因数中最大的那一个； ● 如果自然数 m 是这 n 个自然数的公因数，且这 n 个数的任意公因数都是 m 的因数，就称 m 是这 n 个数的最大用因数。 通常国内的记述方式为 [(a1, a2, ..., an)] ，国际通用的记号为 [g.c.d.(a1, a2, ..., an)] |