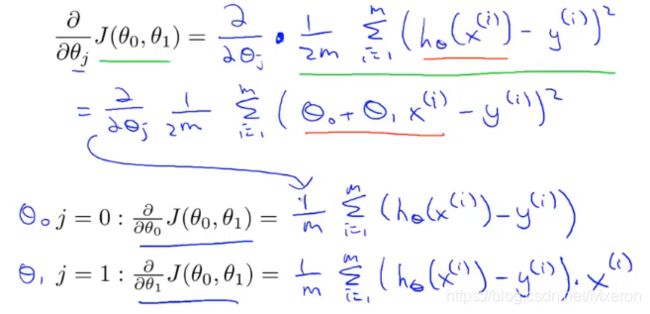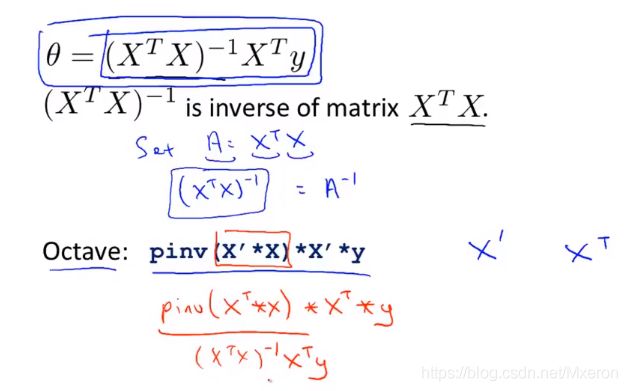吴恩达机器学习学习笔记一：监督与无监督学习、代价函数、梯度下降算法、正规方程算法

一、监督学习（supervised learning）与无监督学习（unsupervised learning）

最常用的两类机器学习算法（Machine learning algorithms）：
1、supervised learning：我们教会计算机做某件事情
2、unsupervised learning：我们让计算机自己学习

学了之后要知道怎么使用这些工具！

Supervised Learning（监督学习）

我们给算法一个数据集，其中包含了正确答案，算法的目的就是给出更多的正确答案。
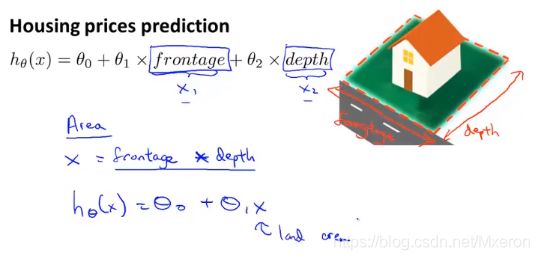
例：出售房价估价？

回归问题

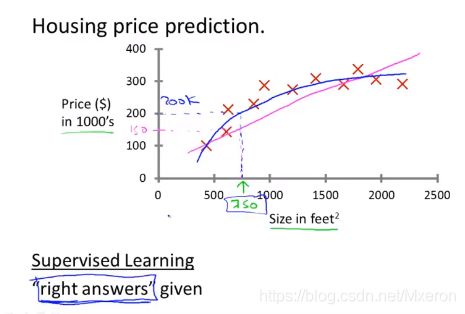
上述问题也被称为：回归问题（Regression Problem），我们想要预测连续的数值输出，也就是估价。

分类问题

例：是否为恶性肿瘤？

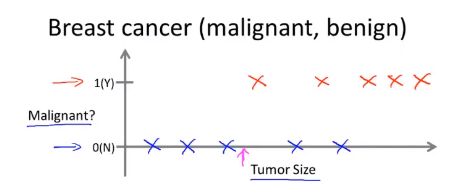
上述问题也被称为：分类问题（Classification Problem），我们设法预测一个离散值（0，1，2，3）输出（即图中的0或1，恶性或良性），这里我们只用了一个特征（属性）来预测，但我们可能会有多个特征！

（两个特征（Age and Tumor Size））

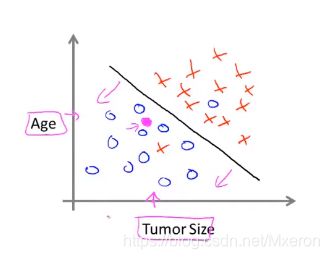
如何处理无穷多个特征？？？

Unsupervised Learning（无监督学习）

我们得到一个数据集，我们不知道要拿它来做什么，也不知道每个数据点究竟是什么，我们只被告知这里有数据集，你能从中找到某种结构吗？

聚类算法

对于给定的数据集，无监督学习算法可以将数据分为两个不同的簇（团）（clusters），如下图：

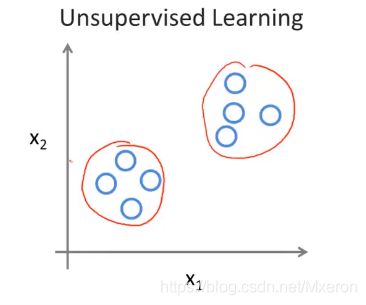
这就是聚类算法（Clustering Algorithm），用于很多地方，例如谷歌新闻，它从网络上收集几十万份新闻数据，然后自动地将他们分簇（聚类），同一主题的新闻被显示在一起。

鸡尾酒会算法

鸡尾酒会算法：给它一个音频，它会分析出有几个音源，并试图将他们逐一呈现。（处理音频、分离音频）

使用Octave学习如何实现之后将要学习的算法，在硅谷，很多的机器学习算法，都会先用Octave建立软件模型，因为在Octave中实现这些学习算法的速度很快！之后才将其迁移到C++、Java或其他编译环境。
（你也可以在C++、Java、Python中实现，只是会更加复杂而已）

这里：
1、使用小写字母m表示训练样本的数量
2、使用小写字母x来代表输入变量（variable）（或者说是特征（features））
3、使用小写字母y来代表输出变量（目标变量）
4、使用（x,y）来表示一个训练样本
5、使用（x^(i),y(i))来表示特定的（第i个）训练样本，i用于索引而不是指数

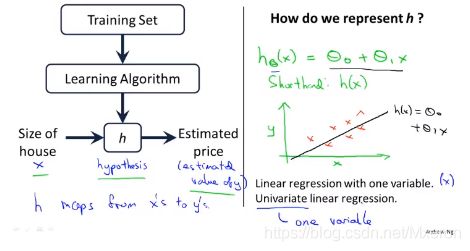
h代表假设函数（hypothesis），作用是把房子的大小作为输入变量（作为x值），而h会输出相应房子的预测y值，即：h是一个引导从x得到y的函数。

怎么样表示h？

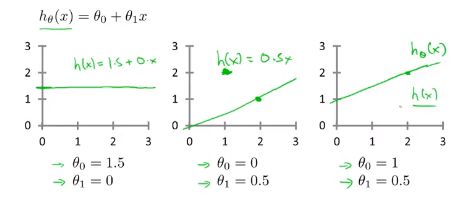
我们会先从**拟合线性函数（线性回归（Linear Regression））**开始，之后拟合更加复杂的。

思想：

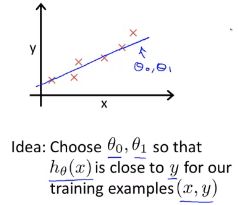
我们需要尽量选择参数值seita0 seita1 使得在训练集中，给出训练集中的x值，我们能合理准确地预测y的值。

目的：minimize J(seita0,seita1）

上述函数也被称作代价函数（cost function），也被称为均方误差函数。
m为训练集的样本容量
预测值和实际值的差的平方除以2m最小
因为对于大多数问题，特别是回归问题，均方误差函数都是一个合理的选择，还有其他代价函数也可以使用，但均方误差函数可能是解决回归问题最常用的手段了。

二、代价函数（Cost Function）

Goal即：优化目标

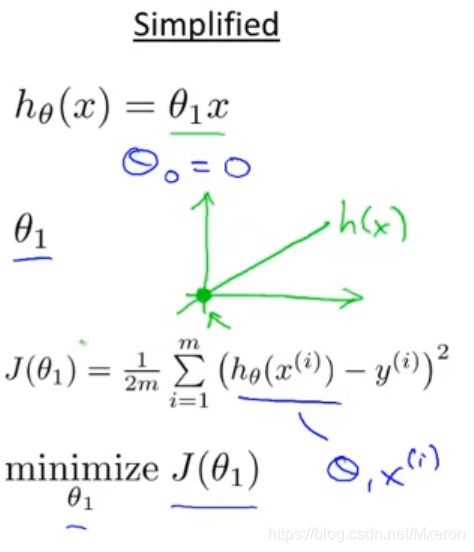
简化后的代价函数：
让seita0=0，只有seita1一个参数

三、用梯度下降算法（Gradient Descent Algorithm）最小化任意函数J

梯度下降算法思路：
1、给两个参数赋两个值开始
2、一点点改变这两个值，来使J(seita0,seita1)减小
3、直到达到我们希望达到的最小值

梯度下降算法可应用于更一般的函数（即多参数下的函数，讲解中只用两个参数）

梯度下降算法的定义：

（Simultaneous update：同时更新）
在这个算法中需要对seita0、seita1进行同步更新

↑没有做到同步更新！

α：学习率（learning rate），用于控制，当梯度下降时，我们迈出多大的步子（以多大的步伐逼近最小值）。（越大梯度下降就越快）

在梯度下降算法中，当我们接近局部最低点时，梯度下降算法会自动采取更小的幅度（学习率不会变），这是因为越接近最低点时，斜率越接近于0，导数值会自动变得越来越小。（所以也就不需要在过程中多次改变学习率）

四、线性回归算法（代价函数+梯度下降算法）

将梯度下降算法应用到最小化平方差代价函数

（需要对seita0和seita1进行同步更新！）

注意线性回归的代价函数（Cost function for linear regression）总是呈现弓形

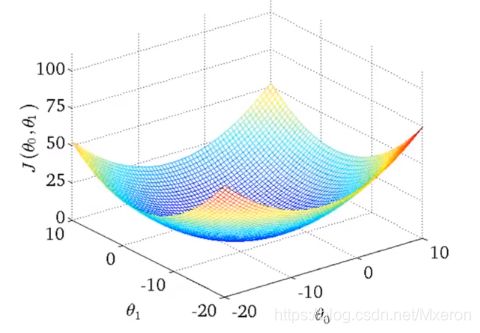
它只有一个全局最优解，当你计算这种代价函数的梯度下降，只要你用的是线性回归，它总是会收敛到全局最优。

以上算法也被称作：Batch梯度下降算法，每次都会遍历一整个数据集，适用于更大的数据集（之后会有只遍历部分子集）

至此：恭喜你学习了第一个机器学习算法！

五、使用梯度下降算法处理多元线性回归

改写假设函数：

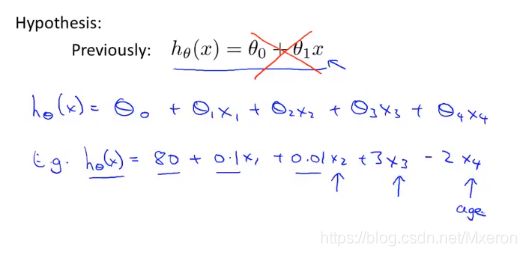
多元线性回归，用向量来表达：

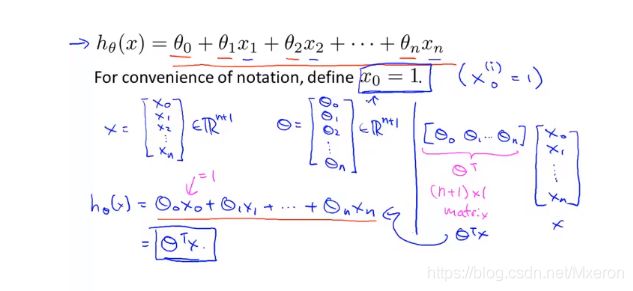
如何设定假设函数的参数？如何使用梯度下降算法来处理多元线性回归

六、多元梯度下降算法优化

特征缩放法（Feature Scaling）

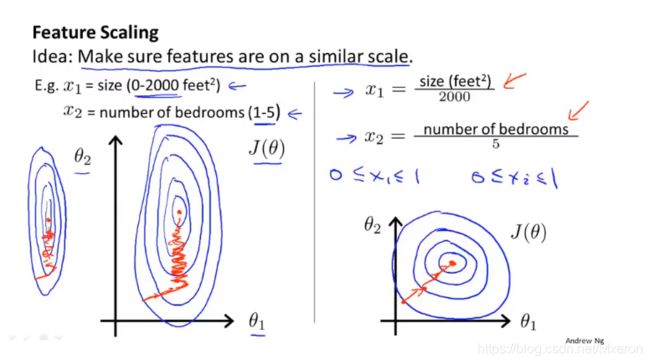
为什么要采用特征缩放法？
因为可能某些特征的范围区间差距太大，导致梯度下降时收敛较慢，采用后，可以使其更快地收敛。

通常，我们采用特征缩放法，将特征的取值约束到-1 到 +1 的范围内（只要接近于这个范围即可）
如果范围太小要进行放大，范围太大要进行放小！特征缩放不用太精确，只是为了使梯度算法下降得快一点，收敛所需的迭代次数减少。

均值归一化（Mean Normalization）

具体做法就是：如果你有一个特征xi你就用xi−μi来替换。**这样做的目的是为了让你的特征值具有为0的平均值。**很明显 我们不需要把这一步应用到x0中，因为x0总是等于1的，所以它不可能有为0的的平均值。

如何选择学习率α（Learning Rate）

Debugging：
1、画出min(J(seita))与迭代次数的图像，可以根据图像观察梯度下降算法是否在正确地允许。

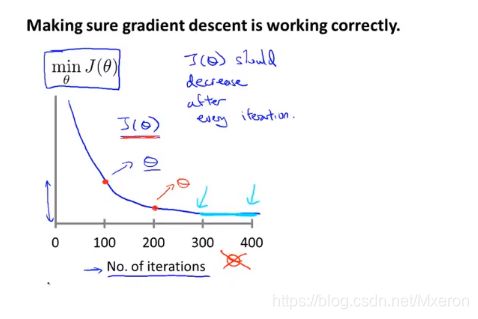
（不同问题下的迭代次数是不一样的）
2、也可以让程序自己判断，例如：设置当J(seita)在迭代一次后只下降了小于一个很小的值，此时则判断它收敛完成。（但是选择一个合适的阈值是很困难的）

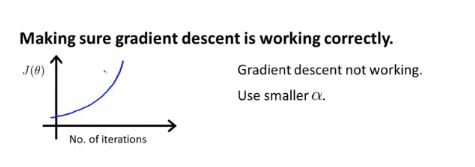
如图的情况，需要使用更小的学习率！

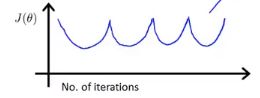
波动曲线也使用更小的学习率。

只要学习率α足够小，那么每次迭代之后代价函数J(seita)都会下降！但也不能太小，如果太小会导致梯度下降算法收敛很慢！

七、特征和多项式回归（Features and Polynomial Regression）

以房价预测为例：

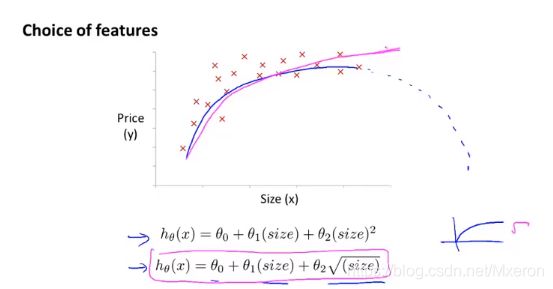
选什么为你的特征，取决于你用什么样的角度去审视问题，你可以用两个特征（长宽）也可以用一个特征（占地面积）来作为假设函数的参数，通过设定新的特征你可能会得到一个更好的模型。

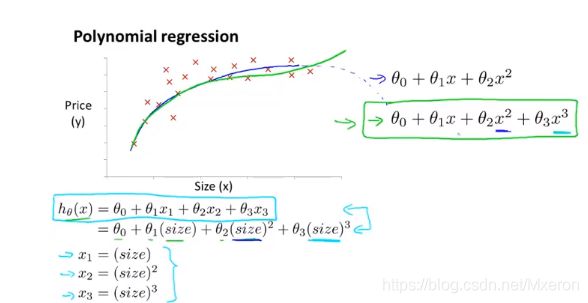
与特征选择密切相关的一个概念称为：多项式回归（多项式模型）

那么，我们如何将模型与数据进行拟合呢？

使用多元线性回归的方法，我们可以对算法做一个简单的修改来实现它。

图中的x1可以是房子面积，x2是房子面积的平方，x3是房子面积的立方，选用这三个特征，再应用线性回归的方法就可以拟合上面这些数据。
注意：如果这么选择特征，那么你的特征缩放就变得更加重要了！这样才能将值的范围变得具有可比性。

也可以采用方根来拟合

八、正规方程（Normal Equation）

对于某些线性回归问题，它会给我们更好的方法来求得参数seita的最优解。

之前的梯度下降算法，需要我们一次次的迭代来寻找最优解，正规方程可以直接一次性求解最优解。

当然它也有缺点，在谈这些之前，我们先对它有一个直观的了解。

对于一个二次函数我们怎么找最优解呢？

对它求导然后令它的导为0…求出最优解seita（seita是实数的情况下），但我们面临的很多问题中，seita不再是实数，而是一个n+1维的参数向量（从seita0到seitan)，这时我们就需要求出这个参数向量的最优解。


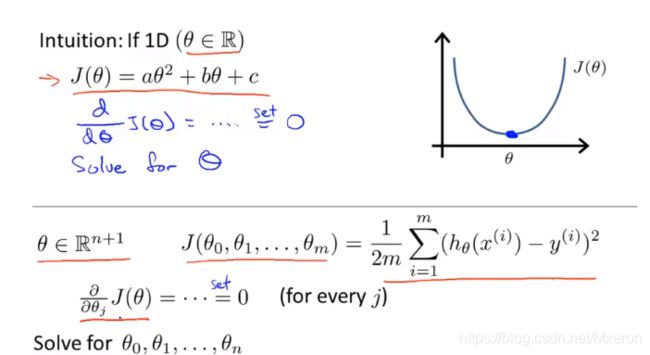
图中的

即是使得代价函数最小化的seita值！

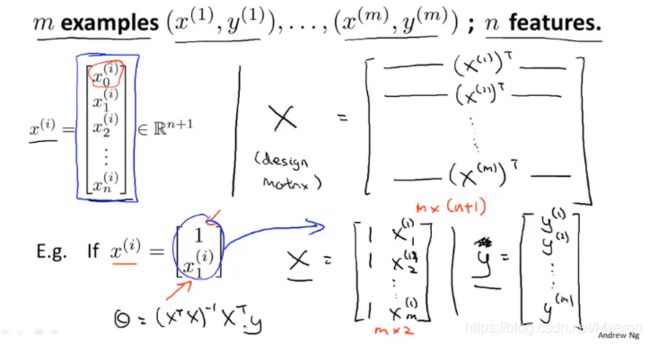
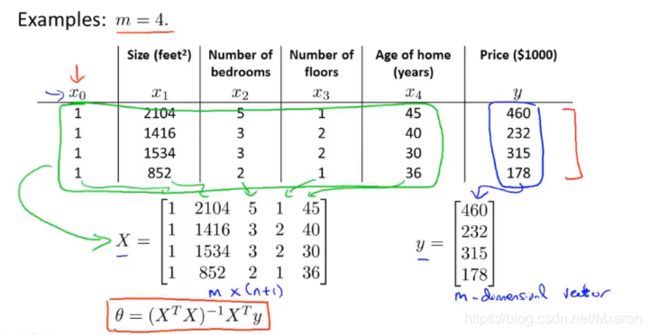
如何构建公式中的X和Y？

每个训练样本给出一个这样的特征向量（即图中x(i)矩阵，它是一个n+1维向量，有n个特征值，x0是seita0，它是多项式中的变化常数不属于任何一个x的系数，所以n个特征值对应着n+1维向量）

之后将每一个训练样本的特征向量转置，构成了一个X构造矩阵（Design Matrix），Y就是训练样本结果矩阵向量。

在构建完X构造矩阵和Y后，就可以使用公式了！

为什么不能把逆矩阵展开化简？
因为X转置乘X一定是方阵，但是不能保证X是方阵！

如果你采用正规方程算法，那么就不需要特征缩放；但如果采用梯度下降算法特征缩放任然很重要。

那么，什么时候用梯度下降？什么时候用正规方程？

梯度下降：需要选择学习率，需要很多次迭代
正规方程：不需要选择学习率，也不需要迭代

但：
梯度下降算法在有很多特征（注意是特征，不是训练样本！）的情况下，任然表现得很好，但如果选用正规方程，速度会变慢！

多少特征算多呢？
百位千位特征对现在的计算机没有太大问题，但如果有上万的特征可能就需要考虑使用梯度下降算法了！

在之后的学习中，会有更多复杂的算法，正规方程不适用，此时梯度下降算法是一个非常有用的算法。

九、正规方程在矩阵不可逆情况下的解决方法

如果X转置X不可逆怎么办？

在Octave中，求矩阵的逆有两个函数（pinv(Pseudo-inverse)伪逆，inv(inverse)逆），数学上可以证明，只要你使用pinv函数，它就能计算出你想要的seita值，即使！X转置X是不可逆的！

什么会导致X转置X不可逆？

1、有多余的特征（即不允许向量组中的两个向量线性相关），解决方法：去除冗余特征。
2、 有过多的特征（即训练样本的数量小于等于特征的数量），解决方法：删除一部分特征，或使用正则化（Regularization） 之后会进行学习。

总之，不可逆的情况极少发生！发生了使用pinv函数还是可以正确得到结果。