用神经网络实现手写数字识别

用神经网络实现手写数字识别

这是我的第一篇关于神经网络的博客，我们的目的是建立一个全连接的神经网络模型来识别手写数字，希望通过写博客记录自己学习的过程，不断提高。本文主要参考这篇博文
一文弄懂神经网络中的反向传播法

1.准备工作

环境：python 3.7 , pycharm
在开始之前我们需要导入一些模块：

• numpy python中用来进行科学计算的基本软件包
• scipy.special 这是一个常见的激活函数，sigmoid函数
• matplotlib：用于在Python中绘制图表。

如果没有以上库请自行安装。

import numpy as np
import scipy.special
import matplotlib

我们这次实验用到的数据集是MNIST数据集，MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。研究人员已经把图片处理为了字节的形式，所以我们在使用时非常方便。

2.建立模型

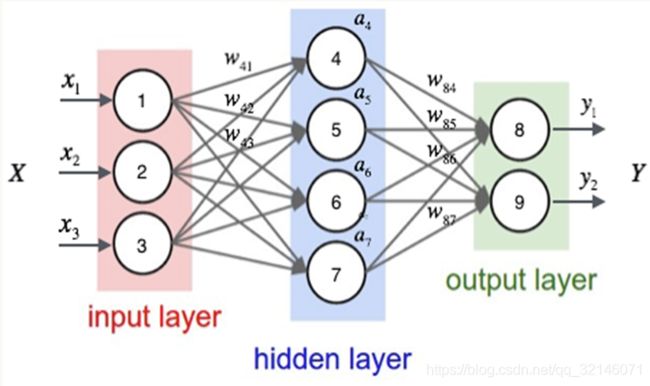
这是我们这次实验的模型，从图中可以看出，我们建立的神经网络由3层组成，分别是输入层，隐藏层，输出层。神经元的个数分别为：

• 输入层神经元：784
• 隐藏层神经元：200
• 输出层神经元：10

神经网络的计算主要分为两个部分，一是正向传播，计算输出值与期望值的误差。我们使用的损失（误差）函数是最简单的函数，激活函数用的是sigmoid函数：
E = T -Y
正向传播过程如上图所示，输入数据分别乘以与之相连的线上的权重再相加，最后再放到sigmoid激活函数中即得到隐藏层的输出，依次类推即计算出了每个输出神经元的输出。通过计算损失函数我们可以知道神经网络的准确性，损失函数越小说明模型拟合的越好。
第二个部分是反向传播过程，这部分主要是通过调整神经网络中的参数，从而提高神经网络的准确性。更新权重利用的是梯度下降法，调整公式如下：

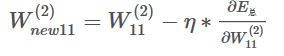
其中n为学习率，在公式中是非常关键的，关系到参数下降的程度，选的太大可能找不到最优值，选的太小训练速度会非常慢。在本文中我们选取n=0.1。如果你需要了解推导过程可以看文章开头提供的博文。

3.代码实现

本实验通过python进行实现，

import numpy as np
import scipy.special
import matplotlib

class neuralNetwork :

    # 用于神经网络初始化
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
        # 输入层节点数
        self.inodes = inputnodes
        # 隐层节点数
        self.hnodes = hiddennodes
        # 输出层节点数
        self.onodes = outputnodes
        # 学习率
        self.lr = learningrate

        # 初始化输入层与隐层之间的权重（ -1 到设置权重 1）
        self.wih = np.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
        # 初始化隐层与输出层之间的权重
        self.who = np.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))

        # 激活函数（Sigmoid（x）=1/1+exp(-x)函数）
        self.activation_function = lambda x: scipy.special.expit(x)

    # 神经网络学习训练
    def train(self, inputs_list, targets_list):
        # 将输入数据转化成二维矩阵(ndmin指定返回的最小维度）
        inputs = np.array(inputs_list, ndmin=2).T
        # 将输入标签转化成二维矩阵
        targets = np.array(targets_list, ndmin=2).T

        # 计算隐层的输入
        hidden_inputs = np.dot(self.wih, inputs)
        # 计算隐层的输出
        hidden_outputs = self.activation_function(hidden_inputs)

        # 计算输出层的输入
        final_inputs = np.dot(self.who, hidden_outputs)
        # 计算输出层的输出
        final_outputs = self.activation_function(final_inputs)

        # 计算输出层误差
        output_errors = targets - final_outputs

        # 计算隐层误差
        hidden_errors = np.dot(self.who.T, output_errors)

        # 更新隐层与输出层之间的权重
        #w = w -德尔塔w = w - E对w的偏导
        self.who += self.lr * np.dot((output_errors * final_outputs * (1.0 - final_outputs)),
                                     np.transpose(hidden_outputs))
        # 更新隐层与输出层之间的权重
        self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), np.transpose(inputs))

    # 神经网络测试
    def test(self, inputs_list):
        # 将输入数据转化成二维矩阵
        inputs = np.array(inputs_list, ndmin=2).T

        # 计算隐层的输入
        hidden_inputs = np.dot(self.wih, inputs)
        # 计算隐层的输出
        hidden_outputs = self.activation_function(hidden_inputs)

        # 计算输出层的输入
        final_inputs = np.dot(self.who, hidden_outputs)
        # 计算输出层的输出
        final_outputs = self.activation_function(final_inputs)

        return final_outputs

if __name__ == "__main__":
    # 初始化 784（28 * 28）个输入节点，100个隐层节点，10个输出节点（0~9）
    input_nodes = 784
    hidden_nodes = 200
    output_nodes = 10

    # 学习率0.1
    learning_rate = 0.1
    # 训练次数
    epochs = 5
    # 初始化神经网络实例
    n = neuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)

    # 读取训练集
    training_data_file = open('mnist_dataset/mnist_train_100.csv', 'r')
    training_data_list = training_data_file.readlines()
    training_data_file.close()

    # 训练数据
    for e in range(epochs):
        for record in training_data_list:
            all_values = record.split(',')
            # 输入数据范围（0.01~1）
            inputs = np.asfarray(all_values[1:]) / 255.0 * 0.99 + 0.01
            # 标记数据（相应标记为0.99，其余0.01）
            targets = np.zeros(output_nodes) + 0.01
            targets[int(all_values[0])] = 0.99
            n.train(inputs, targets)

    # 读取测试数据
    test_data_file = open('mnist_dataset/mnist_test.csv', 'r')
    test_data_list = test_data_file.readlines()
    test_data_file.close()



    # 打印测试数据标签
    count = 0.0
    for record in test_data_list:
        test_data = record.split(',')
        print('原标签：', test_data[0])

    # 生成标签图片
   # image_array = np.asfarray(test_data[1:]).reshape(28, 28)
    #plt.imshow(image_array, cmap='Greys', interpolation='None')


   # plt.show()

    # 利用神经网络预测
        results = n.test(np.asfarray(test_data[1:]) / 255.0 * 0.99 + 0.01)
        pre_label = np.argmax(results)
        print('预测结果：', pre_label)
        if int(pre_label) == int(test_data[0]):
            count = count + 1


    #print(results)
    print(count)
    rating = count/10000
    print("correct rating: %f" % rating)

小结

由于本文是一篇深度学习入门的小实验，目的在于以最快的时间了解深度学习的方法和框架，所以选用的模型，损失函数等比较简单，因此手写数字的识别率不高，只有66%左右。接下来会通过调整超参数，模型的选择等方法来提高识别率。