视觉SLAM十四讲源码的正确打开方式：第3讲 三维空间刚体运动

当你下定决心开始学习SLAM时，看到《视觉SLAM十四讲》的你是否欣喜若狂？
当你学完理论知识准备在实践章节大显身手时，发现源码完全不会跑的你又是否一脸懵逼？
不要怕！
和李哈哈一起刷夜，我们一起康康每讲的实践部分，到底怎么玩。

写在前面的话

和很多初学SLAM的小伙伴一样，我对SLAM、对Linux，甚至对C++都不清楚
看了看SLAM十四讲感觉突然有点感觉的时候，实践部分又完全无从下手
针对以上这种情况，我决定将自己完成实践部分作业的过程分享出来
希望那些和我一样刚开始学习SLAM的小伙伴，能够与我产生共鸣
如果对你能有一丢丢帮助，⚽️观众老爷们点个赞

其他各讲实践索引

你可以从这里直接跳转到其他讲的实践讲解:
视觉SLAM十四讲源码的正确打开方式：第1讲 预备知识
视觉SLAM十四讲源码的正确打开方式：第2讲 初识SLAM
视觉SLAM十四讲源码的正确打开方式：第3讲 三维空间刚体运动
李哈哈视觉SLAM十四讲源码的正确打开方式：第4讲 李群和李代数

实践3.2：Eigen

把从GitHub上下载的源码打开，把其中的ch3文件夹拷贝到桌面
如果不知道源码在哪里/怎么下载，可以从索引查看第1讲的内容
我习惯将需要用到的文件拷贝到桌面或桌面的某个文件夹进行测试

---

本节将讲解如何使用Eigen表示矩阵和向量，在下一节的实践引申至旋转矩阵与变换矩阵的计算。
本节的代码在ch3/useEigen中
Eigen 是一个 C++ 开源线性代数库。它提供了快速的有关矩阵的线性代数运算，还
包括解方程等功能。许多上层的软件库也使用Eigen进行矩阵运算，包括 g2o、Sophus 等。

安装Eigen

安装Eigen的方法书上写的直接用就没啥问题（我就是这么装的）
终端输入：

sudo apt-get install libeigen3-dev

Eigen的头文件默认位置为"/usr/include/eigen3"，可以命令行输入以下指令查看电脑安装的位置：

sudo updatedb
locate eigen3

作者提到，Eigen的特殊支出在于，它是纯用头文件搭建起来的库（一般的库应该有头文件&库文件）
所以，在使用时，只需要引入Eigen的头文件，而不需要链接库文件

编译工程

说到这一步，我就来精神了昂！
从何说起呢？
很久很久之前，当我开心地打开ch3这个文件夹，以为简单的编译运行就能跑了
然而这个文件的结构完全让我不知所措
最关键的是，书上写的用来指导编译这个程序的CMakeList.txt只有一句话：

include_directories("/usr/include/eigen3")

但是我打开的CMakeList.txt长这个样子：

cmake_minimum_required(VERSION 2.8)
project(useEigen)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")

# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(eigenMatrix eigenMatrix.cpp)

更离谱的是，ch3里边有四个实践的文件夹：

刚刚提到的CMakeList.txt是useEigen这个文件夹里的，外边居然还有一个CMakeList.txt！
这和我在第2讲看到的工程结构完全不一样啊！
直觉告诉我，作者把一整讲的所有源码都放在了一起，用最外层的CMakeList.txt统一调度
后来看来确实如此
看到这里的时候，我果断停下滚去学CMake了
学习的成果在这里：（这篇文章我觉得自己写的还是不错的，起码花里胡哨的）
CMake自学记录，看完保证你知道CMake怎么玩！！！
非常希望大家粗略的看一下上文，找到里边提到的教程自己做做demo试试看
毕竟迟早要学的嘛
学成归来，开始编译工作，我的方法是在根目录创建一个build文件夹，用来存放编译生成的中间文件：（根目录就是打开ch3之后所在的地方）

以useEigen目录为例，此时该目录文件如下：

在build目录下打开终端，使用编译指令：

cmake ..

该指令后边的两个.是指对上一级目录进行cmake
此时build目录下生成了useEigen目录，其内容如下：

之后我们仍在build目录下，使用编译指令：

make

这时build目录下的useEigen目录如下：

可以看到生成了可执行文件eigenMatrix
至此运行前的编译准备过程就完成了

---

简单说一下这两个指令在干嘛
cmake：根据CMakeList.txt的内容生成编译文件CMakeFiles
make：根据CMakeFiles以及源文件生成可执行文件
由于我们创建了一个build文件夹，所以编译的中间文件及生成的可执行文件保存在了buil目录下
这样说可能不是完全正确，因为我对在build目录下编译的原理还不是很清楚，后续搞懂了回来填坑
应该要再创建一个bin目录来把可执行文件放进去统一管理，但这里先不考虑这个了，抓住主要矛盾就好啦

运行useEigen

使用./命令来运行二进制可执行文件，具体运行方法可以输入以下指令：

./useEigen/eigenMatrix 

在命令行中输入指令效果如下：
关于代码的讲解可以参照这篇还不存在的文章
实践3.2：Eigen
师傅别念了，已经在写了啦
关于本节的代码，我加了一丢丢注释，贴在下边啦：

#include 

using namespace std; //使用std名称空间

#include 
// Eigen 核心部分
#include 
// 稠密矩阵的代数运算（逆，特征值等）
#include 

using namespace Eigen; //使用Eigen名称空间

#define MATRIX_SIZE 50

/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/

int main(int argc, char **argv)
{
     
     // Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
     // 声明一个2*3的float矩阵
     Matrix<float, 2, 3> matrix_23;

     // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix
     // 例如 Vector3d 实质上是 Eigen::Matrix，即三维向量
     Vector3d v_3d; //注意这里的元素是double类型哦，这里的d表示double，改为f就是float
     // 这是一样的
     Matrix<float, 3, 1> vd_3d;

     // Matrix3d 实质上是 Eigen::Matrix
     Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零

     // 如果不确定矩阵大小，可以使用动态大小的矩阵
     Matrix<double, Dynamic, Dynamic> matrix_dynamic;
     // 更简单的
     MatrixXd matrix_x;
     // 这种类型还有很多，我们不一一列举

     // 下面是对Eigen阵的操作
     // 输入数据（初始化）
     matrix_23 << 1, 2, 3, 4, 5, 6;
     // 输出
     cout << "matrix 2x3 from 1 to 6: \n"
          << matrix_23 << endl;

     // 用()访问矩阵中的元素，元素从0开始计数
     cout << "print matrix 2x3: " << endl;
     for (int i = 0; i < 2; i++)
     {
     
          for (int j = 0; j < 3; j++)
               cout << matrix_23(i, j) << "\t";
          cout << endl;
     }

     // 矩阵和向量相乘（实际上仍是矩阵和矩阵）
     v_3d << 3, 2, 1;
     v_3d(0,0) = 100;//!自己写的赋值
     vd_3d << 4, 5, 6;

     // 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的
     // Matrix result_wrong_type = matrix_23 * v_3d;
     // 应该显式转换
     Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
     cout << "[1,2,3;4,5,6]*[100,2,1]=" << result.transpose() << endl;//此时列向量v_3d第一个元素是100

     Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
     cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl;

     // 同样你不能搞错矩阵的维度
     // 试着取消下面的注释，看看Eigen会报什么错
     // Eigen::Matrix result_wrong_dimension = matrix_23.cast() * v_3d;

     // 一些矩阵运算
     // 四则运算就不演示了，直接用+-*/即可。
     matrix_33 = Matrix3d::Random(); // 随机数矩阵
     cout << "random matrix: \n"
          << matrix_33 << endl;
     cout << "transpose: \n"
          << matrix_33.transpose() << endl;          // 转置
     cout << "sum: " << matrix_33.sum() << endl;     // 各元素和
     cout << "trace: " << matrix_33.trace() << endl; // 迹
     cout << "times 10: \n"
          << 10 * matrix_33 << endl; // 数乘
     cout << "inverse: \n"
          << matrix_33.inverse() << endl;                // 逆
     cout << "det: " << matrix_33.determinant() << endl; // 行列式

     // 特征值
     // 实对称矩阵可以保证对角化成功
     SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
     cout << "Eigen values = \n"
          << eigen_solver.eigenvalues() << endl;
     cout << "Eigen vectors = \n"
          << eigen_solver.eigenvectors() << endl;

     // 解方程
     // 我们求解 matrix_NN * x = v_Nd 这个方程
     // N的大小在前边的宏里定义，它由随机数生成
     // 直接求逆自然是最直接的，但是求逆运算量大

     Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
     matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证半正定
     Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);

     clock_t time_stt = clock(); // 计时
     // 直接求逆
     Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
     cout << "time of normal inverse is "
          << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;
     cout << "x = " << x.transpose() << endl;

     // 通常用矩阵分解来求，例如QR分解，速度会快很多
     time_stt = clock();
     x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
     cout << "time of Qr decomposition is "
          << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;
     cout << "x = " << x.transpose() << endl;

     // 对于正定矩阵，还可以用cholesky分解来解方程
     time_stt = clock();
     x = matrix_NN.ldlt().solve(v_Nd);
     cout << "time of ldlt decomposition is "
          << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;
     cout << "x = " << x.transpose() << endl;

     return 0;
}

我觉得这里主要列举了Eigen表示矩阵或向量及基本运算的一些方法
后面可以回来看看这里的东西，感觉只有真的手撕起来才知道怎么玩

实践3.6：Eigen几何模块

3.6.1 Eigen几何模块的数据演示

这一节的实践展示了一些几何模块：旋转矩阵、旋转向量、欧拉角、四元数的Eigen代码实现
用这几种旋转方式旋转一个向量v，最后获得了一样的结果
这里不太想看源码具体怎么实现的了，以后用的时候再回来学习补充
把作者告诉我们的注意事项说一下：
程序代码通常和数学表示有一些细微的差别，比如运算符重载
我们可以在程序中直接计算四元数和三维向量的乘法，但是数学上应把向量转化为虚四元数再相乘
代码运行结果如下：

3.6.2 实际的坐标变换例子

在这一节作者给了我们一个实际的坐标变换的例子
简单来说就是已知两个位姿信息和一个位姿下某点的坐标信息，来求另一个位姿下该点的坐标
具体的问题描述就看书吧，我就不用重新打一遍了吧嘻嘻
而打开源代码，发现头都大了
这一节的代码完全没有注释！！！
不要怕，我把我注释好的放在这里，供大家食用：

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;

int main(int argc, char **argv)
{
     
  Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);//定义两个小萝卜自身姿态的两个四元数
  q1.normalize();//?对两个四元数进行归一化
  q2.normalize();
  //定义两个小萝卜的位置的两个三维坐标
  Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);
  Vector3d p1(0.5, 0, 0.2);//用来表示小萝卜一号坐标系下该点坐标（题干给出）
  Vector3d p2; //用来表示小萝卜二号坐标系下该点坐标
  //!下面分别用四元数以及变换矩阵得到小萝卜二号的该点观测信息
  //以下用四元数求解p2坐标
  p2 = q2 * q1.inverse() * (p1 - t1) + t2;//求解p2坐标
  //这里的inverse是相反的意思，也就是求q1的逆矩阵
  //公式为：p2 = q2  * q1^-1 * (p1 - t1) + t2
  cout << "四元数求得的p2坐标" << endl;
  cout << p2 << endl;//列向量显示
  cout << p2.transpose() << endl;//行向量显示，transpose是转置矩阵的意思

  //以下用欧拉矩阵求解p2坐标
  Isometry3d T1w(q1), T2w(q2);//欧式变换矩阵Isometry（虽然称为3d，实质上是4＊4的矩阵）
  T1w.pretranslate(t1);//设置平移向量，我的理解是加入这个平移向量
  T2w.pretranslate(t2);

  Vector3d p3;//用来表示小萝卜二号坐标系下该点坐标（变换矩阵方法）
  p3 = T2w * T1w.inverse() * p1;//求解p3坐标
  cout << "变换矩阵/欧拉矩阵求得的p2坐标" << endl;
  cout << p3.transpose() << endl;
  return 0;
}

基本上代码怎么回事看我的注释和代码就完全没问题了
一定好好看注释啊亲人们
当然细心的你应该已经发现了，我同时写了四元数求解和变换矩阵的求解结果，结果如下：

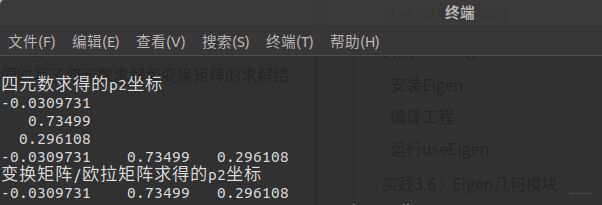
可以看到，二者的结果完全相同
非常有必要的是，你要看看这里的公式推导，戳下边的链接哦：
视觉SLAM十四讲 3.6.2 实际的坐标变换例子代码解析

实践3.7 可视化演示

3.7.1 显示运动轨迹

后边这两节实践还没搞清楚，贴出来演示效果图吧：

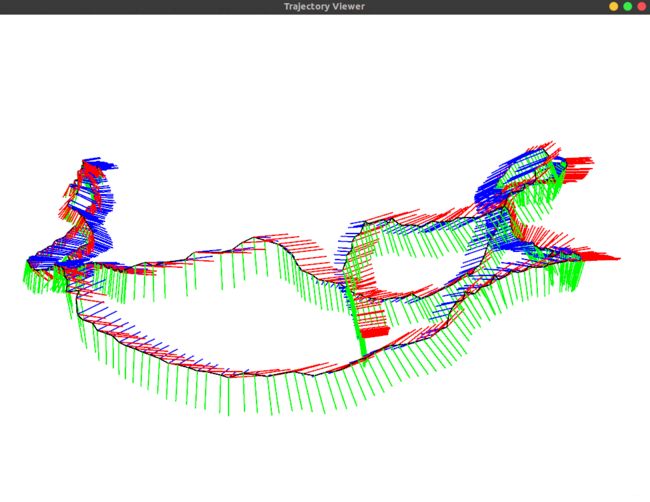
这是很有成就感的一张图，开心！
但是这个程序在运行时遇到了一个bug
直接运行可执行文件，我这里会出现如下的错误：
报错信息为：

cannot find trajectory file at ./example/trajectory.txt

可以理解为程序找不到这个路径下的这个.txt文件
问题就出在该程序的源文件上，也就是基本的.cpp文件，其内部有如下的一句代码：

string trajectory_file = "./examples/trajectory.txt";

他没有在这个路径下找到这个保存有轨迹信息的文件，所以产生了错误
我感觉问题来源应该是我们创建了build文件夹并在里边编译的原因
我的解决办法是直接把文件的完整路径放进去，如下所示：

//这里是一个坑，要把完整路径写上去哦
// path to trajectory file
string trajectory_file = "/home/lihaha/桌面/ch3/examples/trajectory.txt";

这样再运行就没问题啦！

3.7.2 显示相机的位姿

如果你都看到这里了，那说明你一定是个有水平的小可爱
优秀的人都喜欢点赞哦，亲人们给个赞吧，这对我很重要！！！