统计学第八周:参数统计
统计学:参数估计
概念
1.利用总体统计不方便甚至是无法完成的现实状况,采用抽样的方式,利用样本提供的信息来推断总体的特征。
2.点估计:point estimate, 用样本统计量的某个取值直接作为总体参数的估值。
但一个点估计值的可靠性是由它的抽样标准误差来衡量的,这表明一个具体的点估计值无法给出估计的可靠性的度量。
当围绕点估计值构造总体参数的一个区间,这就是区间估计。
3.区间估计:interval estimate ,在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。
根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量。
在区间估计中,由样本统计量所构成的总体参数的估计区间称为置信区间,其中区间的最小值称为置信下限,最大值称为置信上限。
置信水平:将构造置信区间的步骤重复多次,置信区间中包含总体参数真值的次数所占的比例,称为置信水平 confidence level ,也称为置信度或置信系数。
如果用某种方法构造的所有区间中有95%的区间包含总体参数的真值,5%的区间不包括总体参数的真值,那么用该方法构造的区间称为置信水平位95%的置信区间。
-
评价估计量的标准
无偏性:指估计量抽样分布的数学期望等于被估计的总体参数。
设 总 体 参 数 位 θ , 所 选 择 的 估 计 量 为 θ ⃗ , 如 果 E ( θ ⃗ ) = θ , 则 称 θ ⃗ 为 θ 的 无 偏 估 计 量 。 设总体参数位\theta ,所选择的估计量为 \vec{\theta} ,如果E(\vec{\theta}) = \theta,则称\vec{\theta} 为\theta 的无偏估计量。 设总体参数位θ,所选择的估计量为θ,如果E(θ)=θ,则称θ为θ的无偏估计量。

有效性:一个无偏的估计量并不意味着它就非常接近被估计的参数,它还必须与总体参数的离散程度比较小。有效性efficiency是指对同一总体参数的两个无偏估计量,有更小标准差的估计量更有效。 在无偏估计的条件下,估计量的方差越小,估计就越有效。

一致性:指随着样本量的增大,估计量的值越来越接近被估计总体的参数。
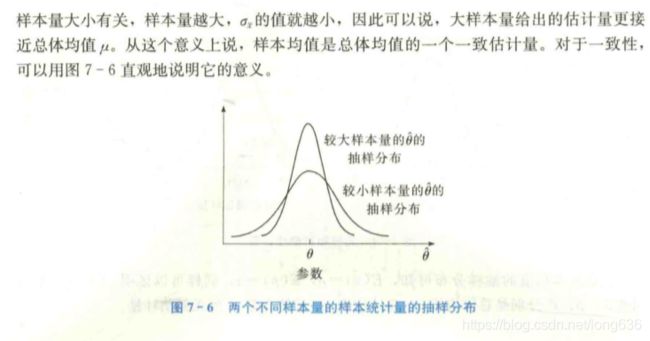
5. 一个总体参数的区间估计
研究一个总体时,关心的参数主要有总体均值,总体比例,总体方差等。那么如何用样本统计量来构造一个总体参数的置信区间。
5.1 总体均值的区间估计
在对总体均值进行区间估计时,需要考虑总体是否为正态分布,总体方差是否已知,用于构造估计量的样本是大样本(30及其以上),还是小样本等情况。
1正态总体/方差已知,或非正态总体/大样本
当总体服从正态分布且方差已知时,或者总体不是正态分布但为大样本时,样本均值的抽样分布均为正态分布,其数学期望为总体均值
μ , 方 差 为 σ 2 / n 。 而 样 本 均 值 经 过 标 准 化 以 后 的 随 机 变 量 服 从 标 准 正 态 分 布 , \mu ,方差为 \sigma^2/n。而样本均值经过标准化以后的随机变量服从标准正态分布, μ,方差为σ2/n。而样本均值经过标准化以后的随机变量服从标准正态分布,
即 z = x ⃗ − μ σ / n 服 从 N ( 0 , 1 ) 即 z=\frac{\vec{x}-\mu}{\sigma/\sqrt{n}}服从N(0,1) 即z=σ/nx−μ服从N(0,1)
在 上 面 公 式 和 正 态 分 布 的 性 质 可 以 看 出 总 体 均 值 μ , 在 1 − a 置 信 水 平 下 的 置 信 区 间 为 x ‾ ± z a / 2 σ n 在上面公式和正态分布的性质可以看出总体均值\mu,在1-a置信水平下的置信区间为\overline{x} \pm z_{a/2}\frac{\sigma}{\sqrt{n}} 在上面公式和正态分布的性质可以看出总体均值μ,在1−a置信水平下的置信区间为x±za/2nσ
x ‾ − z a / 2 σ n 称 为 置 信 下 限 , x ‾ + z a / 2 σ n 称 为 置 信 上 限 , a 也 称 为 风 险 值 \overline{x}-z_{a/2}\frac{\sigma}{\sqrt{n}}称为置信下限,\overline{x}+z_{a/2}\frac{\sigma}{\sqrt{n}}称为置信上限,a也称为风险值 x−za/2nσ称为置信下限,x+za/2nσ称为置信上限,a也称为风险值
它 是 总 体 均 值 不 包 括 在 置 信 区 间 内 的 概 率 ; 1 − a 称 为 置 信 水 平 ; z a / 2 是 标 准 正 态 分 布 右 侧 面 积 为 a / 2 时 的 z 值 ; z a / 2 σ n 是 估 计 总 体 均 值 时 的 估 计 误 差 e s t i m a t e e r r o r 。 它是总体均值不包括在置信区间内的概率;1-a称为置信水平;z_{a/2}是标准正态分布右侧面积为a/2时的z值;z_{a/2}\frac{\sigma}{\sqrt{n}}是估计总体均值时的估计误差 estimate error。 它是总体均值不包括在置信区间内的概率;1−a称为置信水平;za/2是标准正态分布右侧面积为a/2时的z值;za/2nσ是估计总体均值时的估计误差estimateerror。
这就是总体均值的置信区间由两部分组成:点估计值和描述估计量精度的正负值,这个正负值称为估计误差。
如果总体服从正态分布但方差未知,或总体并不服从正态分布,只要是在大样本条件下,总体方差就可以用样本方差来代替,这时总体均值在1-a置信水平下的置信区间可以写为:
x ‾ ± z a / 2 s n , 样 本 方 差 s 2 \overline{x} \pm z_{a/2}\frac{s}{\sqrt{n}} ,样本方差s^2 x±za/2ns,样本方差s2
2正态总体,方差未知,小样本
如果总体服从正态分布,则无论样本量如何,样本均值的抽样分布都服从正态分布。这时只要总体方差已知,即使是在小样本的情况下,也可以按照上面建立总体均值的置信区间。但如果样本方差未知,而且是在小样本情况下,则需要用样本方差代替总体方差,这时样本均值经过标准化以后的随机变量服从自由度为(n-1)的t分布,即:
t = x ‾ − μ s / n 服 从 t ( n − 1 ) 分 布 t=\frac{\overline{x}-\mu}{s/\sqrt{n}}服从t(n-1)分布 t=s/nx−μ服从t(n−1)分布
需要采用t分布来建立总体均值u的置信区间。根据t分布建立的总体均值u在1-a置信水平下的置信区间为:
x ‾ ± t a / 2 s n , t a / 2 是 自 由 度 为 n − 1 时 , t 分 布 中 右 侧 面 积 为 a / 2 时 的 t 值 。 \overline{x}\pm t_{a/2}\frac{s}{\sqrt{n}},t_{a/2}是自由度为n-1时,t分布中右侧面积为a/2时的t值。 x±ta/2ns,ta/2是自由度为n−1时,t分布中右侧面积为a/2时的t值。
总结:
在大样本情况下总体比例的估计问题,由样本比例p的抽样分布可知,当样本量足够大时,比例p的抽样分布可用正态分布近似。
P 的 数 学 期 望 E ( P ) = π ; p 的 方 差 为 σ p 2 = π ( 1 − π ) n 。 样 本 比 例 经 标 准 化 后 的 随 机 变 量 服 从 标 准 正 态 分 布 , 即 P的数学期望E(P)=\pi ;p 的方差为\sigma_p^{2}=\frac{\pi(1-\pi)}{n}。样本比例经标准化后的随机变量服从标准正态分布,即 P的数学期望E(P)=π;p的方差为σp2=nπ(1−π)。样本比例经标准化后的随机变量服从标准正态分布,即
z = p − π π ( 1 − π ) / n 服 从 N ( 0 , 1 ) z=\frac{p-\pi}{\sqrt{\pi(1-\pi)/n}}服从N(0,1) z=π(1−π)/np−π服从N(0,1)
与总体均值的区间估计类似,在样本比例P的基础上加减估计误差
z a / 2 σ p , 即 得 总 体 比 例 π 在 1 − a 置 信 水 平 下 得 置 信 区 间 为 p ± z a / 2 π ( 1 − π ) / n z_{a/2}\sigma_p,即得总体比例\pi在1-a置信水平下得置信区间为 p\pm z_{a/2}\sqrt{\pi(1-\pi)/n} za/2σp,即得总体比例π在1−a置信水平下得置信区间为p±za/2π(1−π)/n
用 计 算 总 体 比 例 π 的 置 信 区 间 时 , π 值 应 该 时 已 知 的 。 但 实 际 情 况 不 然 , π 值 恰 好 是 要 估 计 的 , 所 以 需 用 样 本 比 例 p 来 代 替 π 。 这 时 , 总 体 比 例 的 置 信 区 间 可 表 示 为 p ± z a / 2 p ( 1 − p ) / n 用计算总体比例\pi 的置信区间时,\pi 值应该时已知的。但实际情况不然,\pi值恰好是要估计的,所以需用样本比例p来代替\pi。这时,总体比例的置信区间可表示为 p\pm z_{a/2}\sqrt{p(1-p)/n} 用计算总体比例π的置信区间时,π值应该时已知的。但实际情况不然,π值恰好是要估计的,所以需用样本比例p来代替π。这时,总体比例的置信区间可表示为p±za/2p(1−p)/n
式 子 中 , a 是 显 著 性 水 平 , z a / 2 是 标 准 正 态 分 布 右 侧 面 积 为 a / 2 时 的 z 值 ; z a / 2 p ( 1 − p ) / n 是 估 计 总 体 比 例 时 的 估 计 误 差 。 式子中,a是显著性水平,z_{a/2}是标准正态分布右侧面积为a/2时的z值;z_{a/2}\sqrt{p(1-p)/n}是估计总体比例时的估计误差。 式子中,a是显著性水平,za/2是标准正态分布右侧面积为a/2时的z值;za/2p(1−p)/n是估计总体比例时的估计误差。
对 于 总 体 比 例 的 估 计 , 确 定 样 本 量 足 够 大 的 一 般 经 验 规 则 时 : 区 间 p ± 2 p ( 1 − p ) / 2 中 不 包 含 0 或 1 , 或 者 要 求 n p ≥ 5 和 n ( 1 − p ) ≥ 5 对于总体比例的估计,确定样本量足够大的一般经验规则时:区间p\pm2\sqrt{p(1-p)/2}中不包含0或1,或者要求np\geq 5和 n(1-p)\geq5 对于总体比例的估计,确定样本量足够大的一般经验规则时:区间p±2p(1−p)/2中不包含0或1,或者要求np≥5和n(1−p)≥5
5.3 总体方差的区间估计
针对正态总体方差的估计问题:根据样本方差的抽样分布可知,样本方差服从自由度为n-1的卡方分布构造总体方差的置信区间。
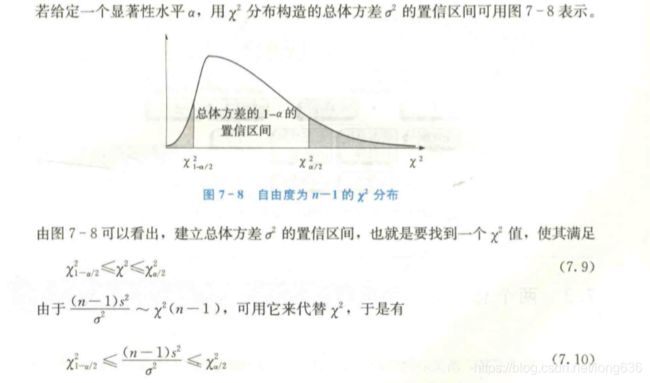
可 推 导 出 总 体 方 差 σ 2 在 1 − a 置 信 水 平 下 的 置 信 区 间 为 , ( n − 1 ) s 2 χ a / 2 2 ≤ σ 2 ≤ ( n − 1 ) s 2 χ 1 − a / 2 2 可推导出总体方差\sigma^2 在1-a置信水平下的置信区间为,\frac{(n-1)s^2}{\chi_{a/2}^{2}}\leq \sigma^2 \leq \frac{(n-1)s^2}{\chi_{1-a/2}^{2}} 可推导出总体方差σ2在1−a置信水平下的置信区间为,χa/22(n−1)s2≤σ2≤χ1−a/22(n−1)s2
-
两个总体参数的区间估计
6.1 两个总体均值之差的区间估计
设 两 个 总 体 的 均 值 分 别 为 μ 1 , μ 2 , 从 两 个 总 体 中 分 别 抽 取 样 本 量 n 1 , n 2 的 两 个 随 机 样 本 , 其 样 本 均 值 分 别 为 x 1 ‾ , ( ‾ x 2 ) 。 两 个 总 体 均 值 之 差 μ 1 − μ 2 的 估 计 量 显 然 是 两 个 样 本 的 均 值 之 差 x 1 ‾ − o v e r l i n e x 2 设两个总体的均值分别为\mu_1,\mu_2,从两个总体中分别抽取样本量n_1,n_2的两个随机样本,其样本均值分别为\overline{x_1},\overline(x_2)。两个总体均值之差\mu_1-\mu_2的估计量显然是两个样本的均值之差 \overline{x_1}-overline{x_2} 设两个总体的均值分别为μ1,μ2,从两个总体中分别抽取样本量n1,n2的两个随机样本,其样本均值分别为x1,(x2)。两个总体均值之差μ1−μ2的估计量显然是两个样本的均值之差x1−overlinex2
大样本的估计:如果两个样本是从两个总体中独立抽取的,即一个样本的元素与另一个样本中的元素相互独立,则成为独立样本independent sample 。如果两个总体 都为正态分布,或两个总体不服从正态分布但两个样本都为大样本(样本数均大于等于30),根据样本抽样的知识可知,两个样本均值之差的抽样分布服从期望值为
μ 1 − μ 2 , 方 差 为 ( σ 1 2 n 1 + σ 2 2 n 2 ) 等 正 态 分 布 , 两 个 样 本 均 值 之 差 经 标 准 化 后 服 从 标 准 正 态 分 布 , 即 z = ( x 1 ‾ − x 2 ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n 1 + σ 2 2 n 2 , 服 从 N ( 0 , 1 ) \mu_1-\mu_2,方差为(\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2})等正态分布,两个样本均值之差经标准化后服从标准正态分布,即z=\frac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}},服从N(0,1) μ1−μ2,方差为(n1σ12+n2σ22)等正态分布,两个样本均值之差经标准化后服从标准正态分布,即z=n1σ12+n2σ22(x1−x2)−(μ1−μ2),服从N(0,1)
当两个总体的方差都已知时,两个总体均值之差在1-a置信水平下的置信区间为
( x 1 ‾ − x 2 ‾ ) ± z a / 2 σ 1 2 / n 1 + σ 2 2 / n 2 (\overline{x_1}-\overline{x_2})\pm z_{a/2}\sqrt{\sigma_1^2/n1+\sigma_2^2/n2} (x1−x2)±za/2σ12/n1+σ22/n2
当两个总体的方差均未知时,可用两个样本方差
s 1 2 , s 2 2 来 代 替 , 这 时 , 两 个 总 体 均 值 之 差 μ 1 − μ 2 在 1 − a 置 信 水 平 下 的 置 信 区 间 为 ( x 1 ‾ − x 2 ‾ ) ± z a / 2 s 1 2 / n 1 + s 2 2 / n 2 s_1^2,s_2^2来代替,这时,两个总体均值之差\mu_1-\mu_2在1-a置信水平下的置信区间为 (\overline{x_1}-\overline{x_2})\pm z_{a/2}\sqrt{s_1^2/n_1+s_2^2/n_2} s12,s22来代替,这时,两个总体均值之差μ1−μ2在1−a置信水平下的置信区间为(x1−x2)±za/2s12/n1+s22/n2
小样本的估计:在两个样本都为小样本的情况下,为估计两个总体的均值之差,需要做出一下假定(1)两个总体都服从正态分布;(2)两个随机样本独立分别抽自两个总体。这里分为两个情况,一种是两个总体方差已知,另一种时方差未知:
使用匹配样本进行估计时,分为大样本条件,和小样本情况:
大样本条件,两个总体均值之差
μ d = μ 1 − μ 2 在 1 − a 置 信 水 平 下 的 置 信 区 间 为 d ‾ ± z a / 2 σ d n , d 表 示 两 个 匹 配 样 本 对 应 数 据 的 插 值 ; d ‾ 表 示 各 差 值 的 均 值 , σ d 表 示 各 差 值 的 标 准 差 。 当 总 体 的 σ d 未 知 时 , 可 用 样 本 差 值 的 标 准 差 s d 代 替 \mu_d=\mu_1-\mu_2 在1-a置信水平下的置信区间为 \overline{d}\pm z_{a/2}\frac{\sigma_d}{\sqrt{n}},d表示两个匹配样本对应数据的插值;\overline{d}表示各差值的均值,\sigma_d表示各差值的标准差。当总体的\sigma_d未知时,可用样本差值的标准差s_d代替 μd=μ1−μ2在1−a置信水平下的置信区间为d±za/2nσd,d表示两个匹配样本对应数据的插值;d表示各差值的均值,σd表示各差值的标准差。当总体的σd未知时,可用样本差值的标准差sd代替
小样本情况下,假定两个总体各观察值的配对差服从正态分布。两个总体均值之差
μ d = μ 1 − μ 2 在 1 − a 置 信 水 平 下 的 置 信 区 间 为 d ‾ ± t a / 2 ( n − 1 ) s d n \mu_d=\mu_1-\mu_2 在1-a置信水平下的置信区间为 \overline{d}\pm t_{a/2}(n-1)\frac{s_d}{\sqrt{n}} μd=μ1−μ2在1−a置信水平下的置信区间为d±ta/2(n−1)nsd
6.3 两个总体比例之差的区间估计
由样本比例的抽样分布可知,从两个二项总体中抽出两个独立的样本,则两个样本比例之差的抽样分布服从正态分布。两个样本的比例之差经标准化后服从标准正态分布,即
Z = ( p 1 − p 2 ) − ( π 1 − π 2 ) π 1 ( 1 − π ) n 1 + π 2 ( 1 − π 2 ) n 2 Z=\frac{(p_1-p_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\pi_1(1-\pi)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}}} Z=n1π1(1−π)+n2π2(1−π2)(p1−p2)−(π1−π2)
当总体比例未知时,可用样本比例p1和p2来代替,因此正态分布建立的两个总体比例之差在1-a置信水平下的置信区间为:
( p 1 − p 2 ) ± z a / 2 p 1 ( 1 − p 1 ) n 1 + p 2 ( 1 − p 2 ) n 2 (p_1-p_2)\pm z_{a/2}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}} (p1−p2)±za/2n1p1(1−p1)+n2p2(1−p2)
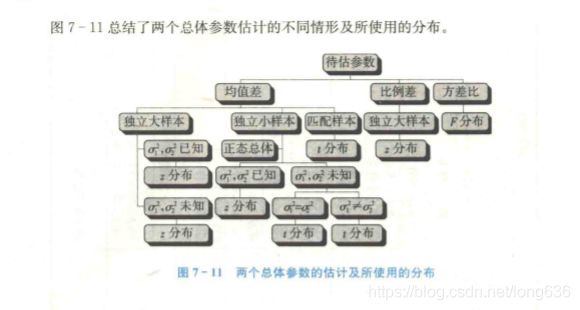
6.4 两个总体方差比的区间估计
由于两个样本方差比的抽样分布服从
F ( n 1 − 1 , n 2 − 1 ) 分 布 , 因 此 可 用 F 分 布 来 构 造 两 个 总 体 方 差 比 σ 1 2 σ 2 2 的 置 信 区 间 F(n_1-1,n_2-1)分布,因此可用F分布来构造两个总体方差比\frac{\sigma_1^2}{\sigma_2^2}的置信区间 F(n1−1,n2−1)分布,因此可用F分布来构造两个总体方差比σ22σ12的置信区间

-
样本量的确定
7.1 估计总体均值时样本量的确定






