题解 2020级HAUT新生周赛(二)
写在读前:
- 本文主要面对广大c语言初学者,文中除部分特例代码采用c++书写外,大部分代码均采用c语言,大家可放心食用。
- 题解内容包含:题目与考点分析、算法思路讲解、参考程序的代码模块设计、注意事项,在以上所有部分都讲解完成后,在一道题的最后会给出参考代码,同时部分题目兼有背景补充或拓展知识,希望可以帮助您全面深入的理解到每一个考点。
- 在每道题的讲解部分会给出各种方法非常详细的讲解,从思想到实现逐步分析,请结合代码与文字一起食用。
- 文中代码均有较为详细的注释,如果在看不懂的情况下,不妨先结合注释转动下灵活的头脑,同时也非常欢迎读者在评论区留下异议或者其他见解。
更新目录:
2020.12.08 修改了部分错别字以及与比赛题目题面不符的内容;
2020.12.10 在文章末尾新添加赛后回顾部分;
这里是目录:
- A. 阿正的忐忑不安
-
-
-
- 参考代码:
-
-
- B. 阿正的学期准备
-
-
-
- 参考代码:
-
- 分支书写:
- 循环书写:
-
-
- C. 阿正的快乐源泉
-
-
-
- 参考代码:
-
-
- D. 阿正的平面行进
-
-
-
- 参考代码:
-
-
- E. 阿正的英语阅读
-
-
-
- 基础方法:
-
- 参考代码:
- 拓展方法:
-
-
- F. 阿正的子母序列
-
-
-
- 参考代码:
-
-
- G. 阿正的排球测试
-
-
-
- 参考代码:
-
-
- H. 阿正的换位排序
-
-
-
- 参考代码:
-
-
- 赛后回顾:
-
-
-
-
- 题目问题总结:
- 代码提交反馈:
- 解题方法分享:
-
-
-
A. 阿正的忐忑不安
题目分析:
给出五个正整数,让你判断前四个数与第五个数的大小关系,若是前四个数大于等于第五个数,则输出一段文本,否则输出另一段文本。
本题意在考察最基本的顺序、分支与逻辑设计,难度属于低级梯队。
思路讲解:
使用一个if结构即可,判断条件位前四个数的和是否大于第五个数。
对于数据类型的选择,本题考察重点并非数据范围,虽然题目中表明了数据的大小,但对分支语句判断等核心算法并未造成影响。采用int类型的整数即可处理所有输入与运算。
代码模块:
输入与初始化——判断——输出
注意事项:
在输出时有一个略坑的地方需要考虑,便是引号的输出。采用printf函数中输出引号需要用到转义字符的输出方法,类似但又不同于换行符,引号的输出需要采用如下格式:
printf(" \" "):
//运行结果:
"
printf函数内写下了一个空格,一个反斜杠,一个引号,一个空格,最后的运行输出结果是一个空格,一个引号,一个空格。
参考代码:
#include拓展与背景补充(引自百度百科):
半角字符:半角字符是指一字符占用一个标准的字符位置,通常的英文字母、数字键、符号键都是半角的,半角的显示内码都是一个字节。
转义字符:所有的ASCII码都可以用“\”加数字(一般是8进制数字)来表示。而C中定义了一些字母前加"\"来表示常见的那些不能显示的ASCII字符,如\0,\t,\n等,就称为转义字符,因为后面的字符,都不是它本来的ASCII字符意思了。
B. 阿正的学期准备
题目分析:
题目给了你几种具有一定规律的优惠方案与阿正所持有的金币数量,我们需要根据金币数量组合出可以获利最大的优惠方案,并输出最后连本带利的金币数量。
我们细看题目中给出的五种优惠方案,可以发现获赠金币与充值金币是成正比的,只有发现了这个规律,分析才能继续进行,我们后续的算法设计皆是建立在此基础之上的。
本题更加灵活的考察了代码设计能力与最简单的贪心思想,选手可以从分支循环等多个角度灵活地书写代码,难度属于低级梯队中最难的一道题。
而何谓”贪心“思想与具体解题方法,请参考下文:
思路讲解:
在获赠金币与充值金币是成正比的基础上,肯定是充值的越多,获利越多。因此我们在已有可以用来充值的金币数固定的情况下,选择充值金币数量多的方案肯定是获利最多的,只要服从”金币数量够,就选最大的“原则,便可以获得最大的利润。
上述叙述就是一个简单的贪心案例,所谓”贪心“,就是当前情况选择可以获利最大的即可,不需要考虑对后续的影响。
在了解了我们设计代码的核心思想后,我们只需要服从上述原则进行设计即可,在这里笔者提供两种思路,读者不必仅局限于此:
在得到可利用最大金币数量后,我们可以自多至少地依次判断金币数量是否满足优惠条件,即从充值金币数量最大的开始判断,如果符合优惠条件,那么便将此项优惠记录,并减少已有的金币数量,继而判断下一项优惠是否满足,直至五项优惠全部判断完。
上文叙述了采用纯分支语句的判断方法,我们按照从多到少的顺序写下五个分支语句便可。同时,我们也可以将这些参数存储到数组中,然后采用循环依次判断是否符合优惠条件:
首先建立两个数组分别来存储充值所需金额与对应的获利金额,此处要注意,我们循环的方向要与上文分支中判断的方向一致,即仍然从大到小进行判断,所以我们在存储数据时可以将数据倒置一下,即将第五种优惠的参数存储到数组下标位0的位置,将第一种优惠的参数存储到数组下标为4的位置。继而,再进行循环依次遍历。
并且对于数据类型的选择,与本次比赛大部分题目相同,本题中明确给出了所有数据均在整形范围内,因此选择整形便足够了。
代码模块:
输入与初始化——数据处理——输出
注意事项:
分支语句的写法不必多言,只需要在进入当前分支后记得减去花费掉的金币数,加上获得的金币数即可。
但若是采用循环的整体框架,则写法更加灵活,可以在循环语句里进行分支判断,也可以进行其他更优的操作。
参考代码:
分支书写:
#include循环书写:
#includeC. 阿正的快乐源泉
题目分析:
题目叙述很长,首先感谢大家有耐心读完 = =。
具有一定算法基础的同学能够轻而易举的发现题目中所给的操作与进行的过程其实就是在模拟 “二分查找” 。(二分查找的介绍详见思路讲解部分)
我们需要在区间[0, Rightmax]中通过二分查找的方法查找值H,并输出进行 “二分操作” 的次数。
并且,由于本题需要输出"二分"的次数便只能通过模拟"二分"的过程来实现,出题人便很仁慈的将数据范围仍然设置为全部在整形内。
本题的意图在于让大家手动模拟二分查找的过程。题目中已经给出了实现的方法,所以大家只需要按部就班的写循环即可,由于许多同学可能从未见过"二分查找",且题面繁琐难懂。。。。故,难度属于中级梯队。
思路讲解:
查找与排序问题是最为基础同时也是最为经典的算法,如何从一段序列中查找到想要的值,或者如何将一段序列按照一定的方法排序,其中大有研究,在此处,我们介绍一种比 “遍历区间每个元素来查找目标” 更快捷的方法——二分查找。
在讲解前,我们首先要明白三个概念,区间的左值、中值、右值,左值即为区间可以取到的最小值,右值即为区间可以取到的最大值,中值即为左右值的平均数,在数轴上表示即为最左边的点, 中间的点,最右边的点,因此称为左、中、右值。
实现二分查找的基础是查找范围必须是有序的,本题中范围即递增排列的从0到Rightmax的整数。
其次,二分操作就是将查找目标值与当前查找区间的中值进行比较,如果当前区间的中值大于目标值,则目标查找值一定在查找区间的左半区间,因此便将查找区间缩小到左半区间,对应题目中"蓝色药丸"的操作,就是将当前区间的右值更改为当前区间的中值。
若当前区间的中值小于查找目标值,则目标值一定在右半区间,那么便指向"红色药丸"的操作,将查找区间缩小到右半区间,将当前左值更新为中值。
重复上述过程,直至使中值mid等于目标值,便是找到了目标值。
为了让大家认识二分查找,出题人不仅在题面中详细叙述了二分查找的过程,也简略了一些步骤。本题中判断是否找到目标值的指标即为中值是否等于目标值。而在不同的问题中,这个指标也不尽相同,大家往往要编写与二分查找结合使用的的check函数来判断当前区间是否可以找到目标值。
介绍完"二分查找",我们结合本题,来具体说明如何编写一份最简单的二分查找的代码:
首先初始化区间的左右值,即为题目中给出的Leftmin与Rightmax,左值一直为0,右值需要题目输入。同时,我们还需要一个变量来记录"二分"的次数。
int times=0,right=maxd,left=0;
//times为记录查找次数的变量,maxd为输入的区间最大的右值,将其赋给right, left则一直为0
之后我们便要模拟 “不断折半” 这个过程,而既然这是个循环执行的过程,那么便一定需要知道边界,二分题目中边界的往往是根据如何进行"折半操作"设置的,而在本题中,我们不断改变左右边界的值,最后使得左右边界相加的中值是目标值的时候就可以退出二分的过程了,结合我们的区间覆盖了从0到Rightmax内的所有制,我们可以想到,这是个在有限步数内的必然结果,所以此处的边界设置只要不在查找到目标之前提前结束,便可以随意设置。
while(left<right){
//...
}
//同时也可以写为while(1)
//while判断括号内的值不为0便可以一直进入,如果while内部没有其他出口的话,这便是一个死循环
//因此采用while(1)的写法, while内部一定要写break的情况
接下来就是 “二分” 的具体操作了,不管是上文还是题面中的叙述都已经非常详细了,此处直接给出具体操作的代码:
int mid=(left+right)/2;
if(mid<standard) left=mid,times++; //红色药丸的操作, 将区间缩小到右半区间, 更新左值
else if(mid>standard) right=mid,times++; //蓝色药丸的操作, 将区间缩小到左半区间, 更新右值
else if(mid==standard) break; //如果找到目标值,那么便直接退出循环
//else if(mid==standard) return times; //如果采用函数的写法,也可以直接退出二分函数
至此,将上述代码组合起来,便是一个最基本的,完整的二分查找了,也是本题的标准程序。
模块设计:
输入与初始化——查找——输出
注意事项:
再次强调,本题目中出现的二分查找是最最最简单的二分查找,实际中二分查找的应用更加广泛也更加灵活,本题只是介绍基本的实现过程,万万不可拘泥于本题给出的模板。
参考代码:
#includeD. 阿正的平面行进
题目分析:
给定两个平面坐标,输出两个点位的对应横纵坐标差的绝对值之和。
本题意在考察最基本的代码编写能力,函数调用能力,难度属于低级梯队。
思路讲解:
依旧是所有数据都在整形范围内,只需要计算出两个点位x坐标差的绝对值,y坐标差的绝对值,并相加后输出即可。
模块设计:
输入与初始化——计算——输出
注意事项:
记得对差取绝对值并且带上其所属的
同时如果使用了全局变量,则要避免使用某些意义冲突的变量名称,比如y1(小写),本地编译器可以通过,但oj会报编译错误。
参考代码:
#include拓展背景:
出租车几何或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇,是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。(引自百度百科)
据说曼哈顿距离命名是由于曼哈顿市区高楼林立,两点间没有直线距离,必须沿一个平面的x轴或者y轴走才能到达。
同时在西洋棋的规则中,车(城堡)是以曼哈顿距离来计算棋盘格上的距离。
E. 阿正的英语阅读
题目分析:
给你一段指定要求的英语文本,你需要找到其中出现次数最多的单词并输出。
这道题最初问世的时候并不长这样子,考虑到大家课程进度或许还没有进行到字符串这一章,最终出题人在好 (坏) 心眼的阿树的建议下,将文本的单词范围限制到规定的十个单词内。
本题意在考察大家对字符串的处理能力,包括输入输出、存储以及各种字符串函数的调用,当然由于单词只有10个,大家也可以枚举10个单词出现的次数进行比较即可。但当没有10个限制时,便必须采用字符串处理的方法了。
同时,这道题除了使用char数组与处理char类型函数解决外,还有更加方便但也更为陌生的方法,便是调用c++语言中非常强大的stl函数来解决问题,两种方法在下文中均有提及。
细节在此不表,请参考思路讲解部分,由于部分同学并不熟悉字符串,并且暴力枚举较为繁琐,此题难度属于中级梯队。
由于出题者本意并不是想让大家枚举10个单词比较次数。。。所以这种方法就不介绍了,大家可以直接来学习下面介绍的字符串处理的方法,实在对枚举10个单词的方法有不明白的地方也可以直接私聊我或者在群里讨论。
基础方法:
思路讲解:
第一步先考虑英语文本输入的方式,其本质便是多实例的以空格分隔的字符串输入,如果会用scanf输入字符串,便可以直接scanf()!=EOF即可,但如果不会使用字符串的输入方式,也可以单个单个字符的输入,先完整的输入多个子母凑成一个单词,遇到空格便表明这个单词结束了。之后也可以直接遇到文件末结束即可。
两种输入方法如下:
字符串输入:
char temp[100];
while(scanf("%s",temp)!=EOF){
//...
}
字符输入:
int index=0;
char temp[100],single;
while(scanf("%c",&single)!=EOF){
if(single!=" ") temp[index++]=single;
//如果不是空格,表示这个单词还没有输入完,那么将字母single填充到temp当前的位置上,并且使下标+1
else{
//...
index=0;
}
//如果是空格,便对当前以及输入完成的单词进行后续操作,并在操作完成后将下标置0
}
首先我们需要考虑如何存储出现的子母,我们第一个想到的肯定是char类型的数组,但是一维的char类型数组在空间上是一串连续的序列,我们需要想办法将每个单词分隔开来。
在单词与单词之间添加特殊的标记作为分隔符?不失为一种解决方法。
但当我们继续考虑下去,如何通过char数组来访问每个单词呢?如何对每个单词进行计数呢?这些情况通过一维数组添加标识符的方法来实现均有着较大的困难。
那么我们便继续思考下去,采用二维的char类型数组呢?
使用二维数组,我们首先要考虑的是空间够不够用,这道题中单词最多会出现十种,且每个单词长度最多不超过10,所以二维数组我们可以10*10的空间足够我们使用了。(小白也可以暂时不考虑空间的问题)
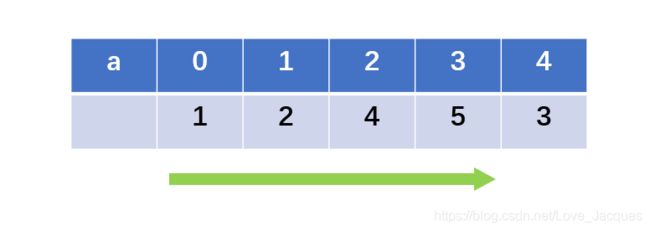
之后我们来考虑二维数组的意义。我们用一个维度来存储不同的单词,然后用下一维度存储每个单词不同的子母,根据题目中的样例,详细的存储单元如下图:

定义二维数组text[][]来存储英语文本,那么在全部输入完成后,text[0]就可以代表 “Azheng” 这个单词,text[0][0]代表的就是 “A” 这个子母,其他位置同理。
这样我们便可以明确用text中一个维度的下标来表示单词的位置,在定义一个counter[] 计数数组,相应位置代表text[][]相应下标位置单词出现的次数就能满足我们这道题的所有操作要求了。即counter[0]代表的是text[0]中 “Azheng” 出现的次数。
这样输入与存储的问题就解决了,下一个问题便是我们如何进行计数?
计数首先要判断这个单词有没有出现过,是否和以前出现过的单词相等,因为我们采用的是二维数组来存储单词,每个单词的子母都可以通过下标来访问,所以我们在读入一个单词后,可以直接遍历已有的text数组,这个单词是否以及被我们存储在text数组里面了,如果找到了,那么对应位置的counter便+1,如果没有,那么就在text内下一个空位存储当前单词即可,同时使counter对应的位置等于1。
计数的问题也解决了,最后我们遍历一遍counter数组,找到counter内的最大值,并输出对应下标处的text内的单词即可。
如果最大值有多个怎么办?此刻我们根据题意,寻找出现最早的单词,便是最早被我们存到text数组内的单词即可。
至此,这道题使用char类型解决的方法已经全部完成,其中涉及到的细节处理请参考注意事项以及下文中的代码。
模块设计:
输入与初始化——计数——输出
注意事项:
在进行算法设计时要考虑时间复杂度与空间复杂度,拿此题为例,空间复杂度在上文已经说明,此处讲一下这道题的空间复杂度:在解题时,由于输入数据的不确定性,我们一般考虑最大时间复杂度,即所有数据都是范围内最大的情况下的时间复杂度。
之后估算时间复杂度,参考代码中执行频数最高的语句,其往往是for循环或者函数的递归,此题中在依次输入不同单词时我们需要采用第一个for循环,在输入后判断判断单词是否与之前重复时,我们需要遍历以前的所有单词,此处采用第二个for循环,而在判断两个单词是否想等时,我们有需要遍历每个字母,此处为第三个for循环。
这三重循环便是这个程序中执行频数最高的语句。随后结合数据范围进行判断,第一重循环最后会有10个不同的单词,第二重循环也是最多出现10个单词,第三重循环每个单词最多10个字符,因此最大的复杂度便是10 * 10 * 10,远远小于题目限制,我们便可以放心进行了。
继而再说一下处理的细节:
- 在判断两个单词是否相等时,如果我们选择while循环,那么便可以不考虑单词长度,遇到text[i1][i2]=="\000"时结束,即字符数组的末尾符;如果我们选择使用for循环,那么我们也可以直接用strlen函数来计算字符串长度。
- 如果当前单词没有出现过,我们可以直接使用字符串复制strcpy函数将其复制到text数组中。
参考代码:
#include
while(scanf("%s",temp)!=EOF){
//采用字符串读入的方法
int address=-1; //adress存当前单词即将放到word中的哪个位置
for(int i=0;i<num;i++){
//num为以前读入的不同的单词个数,遍历它们依次判断
int flag=1,pointer=0;
//必须所有位置上的字母都相等才是旧单词,否则出现一个不相等的,便使flag=0,标记为新单词
while(pointer==0||(temp[pointer-1]!='\000'||word[i][pointer-1]!='\000')){
if(temp[pointer]!=word[i][pointer]){
//不相等,标记为新单词
flag=0;
break;
}else pointer++; //相等,继续判断下一个字母
}
if(flag==1){
//如果是旧单词
address=i; //获取address的值
counter[address]++; //更新counter内对应位置的值
}
}
if(address==-1){
//如果address值没有更新过,即是新单词
strcpy(word[num],temp); //将temp赋到word下一个位置上
counter[num++]=1; //对应counter位置等于1
}
}
int maxd=0,flag=-1; //maxd来存出现最多的次数,flag来存最多者的下标
for(int i=0;i<num;i++){
//遍历出现的单词,寻找出现次数最多者
if(counter[i]>maxd){
//如果遇到更多的
flag=i;
maxd=counter[i]; //更新maxd与flag
}
}
printf("%s\n",word[flag]); //最后输出word中下标为flag处的单词
return 0; //必须return 0;
}
拓展方法:
上文中提到,可以使用C++中强大的stl函数库来快速解决这道题,stl库中含有大量快捷的函数与容器,但此处仅给出使用stl解题的参考代码,有兴趣者可以自行查找资料进行学习。
#includeF. 阿正的子母序列
题目分析:
题面虽然繁琐,但用一句话概括其实非常简明,即为求一个序列中所有不相同的连续非递减子序列个数以及长度和。
本题数据量较大,使用枚举所有连续非递减子序列的方法在时间上并不合理,需要大家估算出时间复杂度,考虑更为快捷的方法。
本题综合性较高,且涉及相对较多的算法思想,难度属于高级梯队。
思路讲解:
下文将从低性能算法的基础上逐步优化,推出最终符合时间限度的方法,若您已经有了部分思路或者想直接跳过方繁琐的文字,不妨参考这篇博客:关于前缀和与差分的讲解。
初看此题,大家首先想到的大多数都是找出所有连续非递减子序列,统计个数以及长度,这样对于长度为10000的序列来说,需要从每个位置上开始判断其为首元素的序列是否递增,递增到哪个位置,这样最低复杂度也是O(n平方)级别的,对于1e4(即1*10的4次方)的数据来说会有超时的风险。
“大部分高性能的算法都是从低性能算法的基础上优化而来的”,换位排序一题中 “你” 这样安慰阿正道,此题中同样如此。
我们首先考虑枚举全部连续非递减子序列的方法最浪费时间的地方在哪里?
我们再来回顾一下枚举全部连续非递减子序列的过程,首先遍历序列的每个元素,枚举出以当前元素为首元素的所有序列,这是第一重循环。其次在确定了首元素之后,需要遍历其后的所有元素,寻找连续非递减序列最长可以延申到哪个位置,多向后延申一个位置,那么符合要求的序列个数便+1,而其前面所有以当前元素为首元素的序列的长度都要+1,这是第二重循环。
在第二重循环计数的过程中,我们其实可以将零碎的多部计数合并成概括性高的一步计数。拿样例为例子,我们计算从a[0]到a[3]这段序列中符合要求的个数时,首先以a[0]为首元素,枚举出{1},{1 2},{1 2 4},{1 2 4 5},其次以a[1]为首元素,枚举出{2},{2 4},{2 4 5}…等等,直至以a[3]为首元素,枚举到{5}。
上述描述本质工作即为:统计长度为4的连续非递减序列所包含的所有连续非递减子序列的个数,加上其本身也算1个。
我们不妨手算一下,从a[0]到a[3]所有符合题意的序列个数为:4 (以a[0]为首元素的个数) + 3 (以a[1]为首元素的个数) + 2 (以a[2]为首元素的个数) + 1 (以a[3]为首元素的个数) 。
那么当我们在母序列中找到一串最长的连续非递减子序列时,例如样例中的{1 2 4 5}与{3}(因为这些序列作为非递减子序列无法再延长)时,只需要计算出这些 “最长” 的子序列包含了多少符合要求的 “子子序列” ,再加上其本身的个数,即可。
而经过我们上文中的手算,我们可以发现这些 “子子序列” 的个数是符合一定规律的。我们倒推一遍,从"最长子序列"末尾元素开始计数:
末尾元素可以构成的"子子序列"无疑只有一个;
倒数第二个元素可以构成的子序列为 {倒二元素本身},{倒二元素,倒一元素},两个‘;
同理,其他位置包含的 “子子序列"个数也与其长度相等;
那么对于长度为n的"最长子序列”,其包含的 “子子序列” 个数便为 1+2+…+n;
对于上式,我们将其称为"n的前缀和",如果你看完了上述长篇大论,还是不能理解的话,可以参考一下这篇讲解:
关于前缀和与差分的讲解。
至此,我们便将 “零碎的多步” 化为了 “高度概括性的一步”,即只找到出母序列中所有 “最长子序列” ,后求出所有"子子序列" 加上其本身的个数即可,“子子序列” 的方法,我们称之为 “前缀和” 。
在解决完个数问题后,我们再来考虑长度如何计算。
在求个数时,我们每发现一个序列,那么便将结果+1;在求长度时,我们每发现一个序列,那么便将结果+这个序列的长度即可。
比如对一个长度为4的连续非递减序列,求其符合要求的子序列个数与长度和:
对应个数公式为: 4 + 3 + 2 + 1 ;
那么其长度和公式便为:(1+2+3+4)+(1+2+3)+(1+2)+(1);
看到这里有没有茅塞顿开的感觉? 又是一个前缀和操作!
模块设计:
预处理、输入与初始化——遍历计算——输出
注意事项:
关于前缀和的详细介绍与使用方法请参考这篇博客:关于前缀和与差分的讲解。
计算前缀和可以在输出与初始化之前进行,我们称之为 “预处理” ,即预先进行一些处理。
在进行长度累加计算时,由于数据范围过大,需要使用长整型类型的变量。
更多的细节将会在代码中以注释的形式给出。
参考代码:
#includeG. 阿正的排球测试
题目分析:
给出一个正整数,让你将其转换为32位的二进制数,空位以0补齐,并在一系列操作后求出给定范围内1的个数与1的总数的比值。
本题意在给大家普及二进制与位运算的相关知识,考察基本的模拟能力,难度属于中级梯队。
思路分析:
纯模拟题,将读入的正整数转化为32位的01数组。
之后根据读入进行相应的操作,最后再统计输出即可。
位运算的相关知识可以参考这篇博客,包括左移右移、与、或、异或。
位运算基本操作。
代码模块:
初始化与输入——处理与计算——输出
注意事项:
- 可以转化为32位的正整数最大范围高达1e10,所以需要开长整型变量进行储存。
- printf函数默认保留四舍五入的输出方式,所以不需要对结果进行再处理。
- 数据细节较多,需要考虑各种边界情况,比如阿正处于0的位置,但是接球半径为31,则可以覆盖全场。
- 输出记得加百分号。
参考代码:
#includeH. 阿正的换位排序
题目分析:
给定你若干个序列,每个序列有一个长度n。对每个序列,若能只交换相邻两个元素的值在 [n(n-1)]/2 -1* 内完成排序,则输出Yes,否则输出No。
本题综合性较高,着重考察思维活跃性,对基础算法的理解程度,难度属于高级梯队。
详细过程见思路讲解。
思路讲解:
首先,使用冒泡排序和选择排序直接计数会超时。
当你看到1e5的数据时,就应该估算到,冒泡排序和选择排序的时间复杂度都是平方级别的,此题行不通。
当然如果你不了解冒泡排序和选择排序,那么根据题目中"提示"的部分,也可以继续进行下去。
如果你熟悉冒泡排序,那就更好了,我们接下来通过讲解冒泡排序来揭示这道题正确的解法。
冒泡排序是个很形象的名字,通过选择序列中的最值,然后将其置于一端,使这个最值 “冒泡” 跑出序列外,重复这个过程便可以完成排序。
每次查找最值的过程都需要遍历一遍序列,所以复杂度是n平方级别的。
冒泡排序的 “将最值置于一端” 这个操作,便可以通过题目中的 “换位” 来实现,不断交换相邻两个元素,使得最大值 “交换” 到序列最端,下一次冒泡便将这个最大值排除在外。假设现在对于一个长度为n的序列,最值处于序列中第i个位置,而序列最右端已经找到了k个最值,那么这个交换次数便为:n-k-i;
在此题中给出了交换次数的临界值,即 [n(n-1)]/2 -1* ,那么我们就要考虑,什么情况下交换次数可以达到临界值?
首先考虑交换次数最多的情况,我们使得冒泡排序的过程中,每次 “冒泡” 的交换次数都达到最多,即最大值处于序列最左端的位置,那么每次交换的次数都为 n-k ,(k为已经完成"冒泡"的次数,0<=k 那么这个总次数便为 1+2+3+…+n-1 = [n(n-1)]/2*。 至此,结果已经明了,只要每次交换使得下一个最值一直出现在最左端,且必须交换到最右端,即**这个序列必须是严格递增的。**只要符合这种情况,那么他的最小交换次数始终比题目要求大1。 那么此题便转换为判断序列是否严格递增了,详细代码见下文。 模块设计: 注意事项: 本次比赛过程中题目出现了两个比较严重的问题,由于出题人的疏忽给部分同学带来了糟糕的比赛体验实属抱歉,在此出题人向所有参赛同学以及工作人员致歉。 在比赛过程中以及赛后的一段时间内,通过分析同学们的提交记录,笔者也在此略作总结: 出现大量 “答案错误0” 的代码,提交错误0的代码可能有两种原因: 具有一定难度的题目提交数量与题面长度成反比(内心略微复杂)。 同时对大家而言,也应该勇于迎难而上,透过现象看本 对于大部分 “输出超限” 的代码,原因有以下几种: 在分析同学们提交记录时,也有一些让笔者眼前一亮的细节,。
而这也是唯一一种,会超出题目要求次数的情况。
读入与初始化——判断——输出
序列必须是严格递增的情况下才会输出no,如果序列中有相等的元素,其可以通过相等的元素减小交换次数,便不足以超过临界值。参考代码:
#include赛后回顾:
题目问题总结:
修改前:

修改后:
代码提交反馈:
<1. 找到bug更改完成后忘了再次用样例测试,导致原本可以通过样例的代码连样例都没通过。
<2. 编写完程序后没有拿样例测试或者没有测试。
不管是哪种情况,都向大家表明了程序编写完成后测试的重要性。完美代码是不存在的,更不用说不用经过调试的完美代码。
同等难度阶级情况下,E题英语阅读的提交数量是G题排球测试的两倍。原因除了G题提示含错误信息对大家理解题目造成了一定影响外,最大的原因即 “题面冗长,设定繁琐” 。这种现象的出现对出题人有一定的启发。。。。(底气不足状) 。
<1. 输入格式有误;
<2. 对于部分样例代码运行时会出现死循环一直输出。解题方法分享:
char temp='"';
printf("Blessings for your %cfouth grade%c in high school!\n",temp,temp);