基于人工萤火虫优化(GSO)算法的函数寻优算法

一、理论基础

2005年，印度学者K.N.Krishnanand和D.Ghose在IEEE群体智能会议上提出了一种新的群智能优化算法，人工萤火虫群优化(Glowworm Swarm Optimization, GSO)算法。2009年，剑桥学者Xin-She Yang根据自然界中萤火虫的发光行为提出萤火虫算法(Firefly Algorithm, FA)。自这两种萤火虫算法提出以来，各国学者对这两种算法进行了研究、改进和应用。经过几年的发展，在连续空间的寻优过程和一些生产调度方面萤火虫算法具有良好的应用前景。
GSO和FA有相似的方面，但在具体实现方面有一定差异。本文具体介绍GSO算法。

二、GSO算法

算法基本思想描述如下：在群体中，每个萤火虫个体被随机分布在目标函数定义的空间中，初始阶段，所有的萤火虫都具有相同的荧光素值和动态决策半径。其中，每个萤火虫个体根据来自动态决策半径内所有邻居萤火虫信号的强弱来决定其移动的方向。萤火虫的动态决策半径会随着在它范围内萤火虫个体的数目而变化，每个萤火虫的荧光素也会随着决策半径内萤火虫个体的数目而改变。萤火虫群优化算法是无记忆的，无需目标函数的全局信息和梯度信息，具有计算速度快，调节参数少，易于实现等特点。萤火虫进化过程中，每次迭代都由萤火虫的部署(初始化)、荧光素更新阶段、移动概率计算阶段、位置更新阶段、邻域范围更新阶段五个部分组成，现分别介绍如下：

1、萤火虫的部署(初始化)

在可行域中随机放置$n$个萤火虫，并赋予每个萤火虫的荧光素为$l_0$，动态决策域为$r_0$。初始化步长$s$，邻域阈值$n_t$，荧光素挥发因子$\rho$，荧光素更新因子(适应度提取比例)$\gamma$，动态决策域更新率(邻域变化率)$\beta$，萤火虫感知域$r_s$，迭代次数$M$。

2、荧光素更新阶段

每个萤火虫个体的荧光素值等于前一时刻的荧光素值加上萤火虫当前适应度值的一定提取比例，然后再减去随着时间挥发掉的一定比例荧光素值，如式(1)所示：$$l_i(t+1)=(1-\rho )l_i(t)+\gamma J(x_i(t+1))\text{\hspace{1em}(1)}$$其中，$l_i(t)$为$t$次迭代时的荧光素浓度大小，$\rho$为荧光素挥发系数，$\gamma$为适应度提取比例，$J(x_i(t))$表示节点$i$在$t$次迭代中的适应度值即目标函数值。

3、移动概率计算阶段

每个萤火虫在具体的移动中，需要根据其决策半径内的所有邻居萤火虫的荧光素浓度大小来决定其移动方向，$P_{ij}(t)$表示$t$时刻(迭代次数)第$i$只萤火虫向第$j$只邻居萤火虫个体进行移动的概率，计算公式如下：$$P_{ij}=\frac{l_j(t)-l_i(t)}{\sum _{k\in N_i(t)}{l}_k(t)-l_i(t)}\text{\hspace{1em}(2)}$$其中，$j\in N_i(t)$，$N_i(t)=\{j:||x_j(t)-x_i(t)||<r_{di}(t);l_i(t)<l_j(t)\}$表示$t$时刻第$i$只萤火虫个体的所有邻居萤火虫的集合，其中，$||x||$代表$x$的范数。

4、位置更新阶段

选择最大的移动概率并进行位置更新：萤火虫$i$朝向它决策半径内具有最大荧光素的萤火虫$j$移动一定步长，那么在$t+1$时刻的移动公式如下：$$x_i(t+1)=x_i(t)+s\frac{x_j(t)-x_i(t)}{||x_j(t)-x_i(t)||}\text{\hspace{1em}(3)}$$其中，$s$为移动步长。

5、邻域范围更新阶段

每个萤火虫采用自适应动态决策半径，在每次迭代的时候根据邻居萤火虫的密度改变它的决策半径，当邻居密度越小，它就加大决策半径以寻找更多的邻居，反之邻居密度越小，就减小决策半径，具体按式(4)进行调整：$$r_{di}(t+1)=min\{r_s,max\{0,r_{di}(t)+\beta (n_t-|N_i(t)|)\}\}\text{\hspace{1em}(4)}$$式中，$\beta$表示领域变化率，$n_t$表示邻居阈值控制萤火虫的邻居数目，$r_s$表示萤火虫感知范围，$r_{di}(t)$表示$t$时刻第$i$只萤火虫的动态决策范围且$0\le r_{di}(t)\le r_s$。
由上步骤可以看出，萤火虫算法每次在其决策半径内依据邻居节点荧光素的强弱来选择移动方向，充分利用了每个萤火虫个体周围的情况来调整自己的位置，具有较好的局部搜索能力。

三、MATLAB程序实现

1、问题描述

Rosenbrock函数的三维立体图如图1所示。

图1 Rosenbrock函数的三维立体图形

求解Rosenbrock函数在$\mathbb{R}=[-3,3]\times [-3,3]$上的最大值。

2、适应度函数

适应度函数fun.m程序如下：

function z = fun(x)   
%% 适应度函数
z = 100.*(x(:, 1).^2-x(:, 2)).^2+(1-x(:, 1)).^2;         

3、主函数

%% 清空环境变量
clc;
clear;

%% 初始化参数
domx = [-3, 3; -3, 3];       % 定义域
rho = 0.9;                   % 荧光素挥发因子
gamma = 0.1;                 % 适应度提取比例
beta = 0.58;                 % 邻域变化率
nt = 6;                      % 邻域阀值(邻域萤火虫数)
s = 0.03;                    % 步长
iot0 = 400;                  % 荧光素初始浓度
rs = 3;                      % 感知半径
r0 = 3;                      % 决策半径
m = size(domx, 1);           % 函数空间维数
n = 50;                      % 萤火虫数量
gaddress = zeros(n, m);      % 分配萤火虫地址空间
gvalue = zeros(n, 1);        % 分配适应度存放空间
ioti = zeros(n, 1);          % 分配荧光素存放空间
rdi = zeros(n, 1);           % 分配萤火虫决策半径存放空间

%% 萤火虫常量初始化
% 初始化地址
for i = 1:m
    gaddress(:, i) = domx(i, 1)+(domx(i, 2)-domx(i, 1))*rand(n, 1);
end
% 初始化荧光素浓度
ioti(:, 1) = iot0;
% 初始化决策半径
rdi(:, 1) = r0;
iter_max = 500;            % 最大迭代次数
t = 1;                     % 迭代计数器
yy = zeros(iter_max, 1);   % 各代最优解

%% 迭代寻优
while t <= iter_max
    % 更新荧光素浓度
    ioti = (1-rho)*ioti+gamma*fun(gaddress);
    % 各萤火虫移动过程开始
    for i = 1:n
        % 决策半径内找更优点
        Nit = [];                 % 存放萤火虫序号
        for j = 1:n
            if norm(gaddress(j, :)-gaddress(i, :)) < rdi(i) && ioti(i, 1) < ioti(j, 1)
                Nit(numel(Nit)+1) = j;
            end
        end
        % 找下一步移动的点开始
        if ~isempty(Nit)           
            Nitioti = ioti(Nit, 1);              % 选出Nit荧光素
            SumNitioti = sum(Nitioti);           % Nit荧光素和
            Molecular = Nitioti-ioti(i, 1);      % 分子
            Denominator = SumNitioti-ioti(i, 1); % 分母
            Pij = Molecular./Denominator;   % 计算Nit各元素被选择概率
            Pij = cumsum(Pij);        % 累计
            Pij = Pij./Pij(end);      % 归一化
            Pos = find(rand < Pij);   % 确定位置
            j = Nit(Pos(1));          % 确定j的位置
            % 萤火虫i向j移动一小步
            gaddress(i, :) = gaddress(i, :)+s*(gaddress(j, :)-gaddress(i, :))/norm(gaddress(j, :)-gaddress(i, :));
            % 边界处理(限制范围)
            gaddress(i, :) = min(gaddress(i, :), domx(1, 2));        
            gaddress(i, :) = max(gaddress(i, :), domx(1, 1)); 
            % 更新决策半径
            rdi(i) = rdi(i)+beta*(nt-length(Nit));
            if rdi(i, 1) < 0
                rdi(i, 1) = 0;
            end
            if rdi(i, 1) > rs
                rdi(i, 1) = rs;
            end
        end
    end
    % 每代最优解存入yy数组内
    yy(t) = max(fun(gaddress));
    % 迭代次数+1
    t = t+1;
end

%% 结果显示
gvalue = fun(gaddress);               % 求各个萤火虫的值
disp('最大值为：')
num = find(gvalue == max(gvalue));    % 最大值序号
MaxValue = max(gvalue)
disp('最优解为：')
BestAddress = gaddress(num, :)
figure;
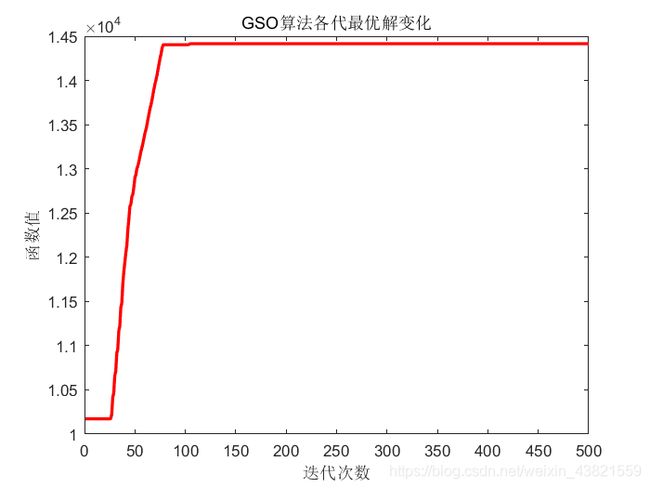
plot(yy, 'r', 'linewidth', 2)
xlabel '迭代次数'; ylabel '函数值';
title 'GSO算法各代最优解变化';

3、结果显示

Command Window中显示的结果为：

最大值为：

MaxValue =

       14416

最优解为：

BestAddress =

    -3    -3

4、绘图

GSO算法各代最优解变化如图2所示。

图2 GSO算法各代最优解变化

四、参考文献

[1] Krishnanand, K. N, Ghose, D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[M]. 2005.
[2] 张谦. 基于群智能算法的无线传感器网络覆盖优化研究[D]. 2015.