深度学习课程设计——波士顿房价预测

 

       基于密集连接神经网络的波士顿房价预测

                               摘  要

神经网络是从信息处理角度对人脑神经元网络进行抽象，建立某种模型，按不同的连接方式组成不同的网络。本文以波士顿房价这一经典数据集为基础，该数据集包含了住宅用地所占比例等13个特征，由于keras.datasets里内置了波士顿房价数据集，所以直接导入。接着对该数据集进行特征标准化，构建包含三层全连接层的网络模型，前两层有64个单元，激活函数为‘relu’，最后一层为1个单元，不加激活层，这样可以预测任意范围的值。编译网络optimizers是‘rmsprop’，loss是‘mse’。然后查看前五个房屋实际价格与预测房屋价格，发现差异较大。然后重新构建一个包含五层的网络模型，前两层是64个单元，后三层分别是32、16、1个单元的全连接层，发现模型性能有所改进，但预测结果还是不太理想。则在模型中引入K交叉折验证方法进行改进，通过调节模型训练轮数、优化器等参数，最后观察模型性能，预测房价与实际房价相差约2400美元，查看前五个预测房屋价格分别是：8.473495，20.397701，22.871258，33.599148，25.75566，与实际房屋价格比较符合。

关键词：波士顿房价；特征标准化；神经网络；K折交叉验证

 

                           

---

                           目录

基于密集连接神经网络的波士顿房价预测

                   摘  要

一、课程设计目的

二、总体思路

三、神经网络实现过程

四、总结

五、参考文献

---

 

一、课程设计目的

在现实的生活中我们经常遇到分类与预测的问题，目标变值通常会受到多个因素的影响，并且不同的因素对于目标变量的影响也不尽相同，因此权重也会不相同，有些因素权重大，有些因素权重小。我们通常会通过已知的因素来预测目标变量的值。

房价是受诸多因素影响的，如人均犯罪率、每个住宅的平均房间数、高速公路可达性等。这些都是影响房子价格的因素。房价明显是连续的取值，故房价预测问题是回归问题。于是我们将通过深度学习来预测波士顿房价。

 

二、总体思路

构建波士顿房价预测任务的神经网络模型步骤：

                                                                         

三、神经网络实现过程

3.1、数据预处理

首先我们需要加载波士顿房价数据，通过观察我们可以发现数据中有404个训练样本和数102个测试样本，每个样本都有13个数值特征，数值特征如下：

属性	数据类型	字段描述
CRIM	Float	城镇人均犯罪率
ZN	Float	占地面积超过2.5万平方英尺的住宅用地比例
INDUS	Float	城镇非零售业务地区的比例
CHAS	Integer	查尔斯河虚拟变量 (= 1 如果土地在河边；否则是0)
NOX	Float	一氧化氮浓度（每1000万份）
RM	Float	平均每居民房数
AGE	Float	在1940年之前建成的所有者占用单位的比例
DIS	Float	五个波士顿就业中心的加权距离
RAD	Integer	辐射状公路的可达性指数
TAX	Float	每10,000美元的全额物业税率
PTRATIO	Float	城镇师生比例
B	Float	1000（Bk - 0.63）^ 2其中Bk是城镇黑人的比例
LSTAT	Float	人口中地位较低人群的百分数
MEDV	Float	（目标变量/类别属性）以1000美元计算的自有住房的中位

我们预测的目标是房屋价格的中位数，单位是千美元。查看测试集前五个数据如下表：

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PIRATIO	B	LSTAT	MEDV
0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296.0	15.3	396.90	4.98	24.0
0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242.0	17.8	396.90	9.14	21.6
0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242.0	17.8	392.83	4.03	34.7
0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222.0	18.7	394.63	2.94	33.4
0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222.0	18.7	396.90	5.33	36.2

 

从样本中数据可以见其取值范围差异较大，若直接输入网络，网络可能会自动适应这种取值范围，但学习会比较困难。因此，我们将对每个特征做标准化，即对每个输入特征减去特征平均值，再除以标准差，这样得到的特征平均值为0，标准差为1

 

###将特征标准化###  
mean = train_data.mean(axis=0)    #计算训练集每一列的均值  
  
std = train_data.std(axis=0)      #计算训练集每一列的方差  
train_data -= mean  
train_data /= std  
test_data -= mean  
test_data /= std 

 3.2、构建网络

本题样本较小，网络结构不复杂，采用三层全连接层。其中密集连接网络（全连接网络）密集连接网络是Dense层的堆叠，它用来处理向量数据(向量批量)。这种网络假设输入特征中没有特定结构：之所以叫做密集连接。是因为Dense层的每个单元都和其他所有单元相连接。这种层试图映射任意两个输入特征之间的关系，它与二维卷积层不同，后者只查看局部关系。

在项目2中介绍过输入数据为向量（数组组成的数组），标签为标量（单个数组），对于这种类型的问题，带有relu激活的全连接层的简单堆叠表现较好。因此前两层的激活函数为‘relu’。最后一层使用纯线性（不加激活层），这样可以预测任意范围内的值。

第一层：全连接层，设置64个单元，激活函数为‘relu’
第二层：全连接层，设置64个单元，激活函数为‘relu’
第三层：全连接层，设置1个单元

编译网络optimizers是‘rmsprop’（），loss是‘mse’（均方误差）。 

def build_model():  
model = models.Sequential()  
model.add(layers.Dense(64,activation='relu',  
input_shape=(train_data.shape[1],)))  
model.add(layers.Dense(64,activation='relu'))  
model.add(layers.Dense(1))  
model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])  
return model  

3.3、模型评测

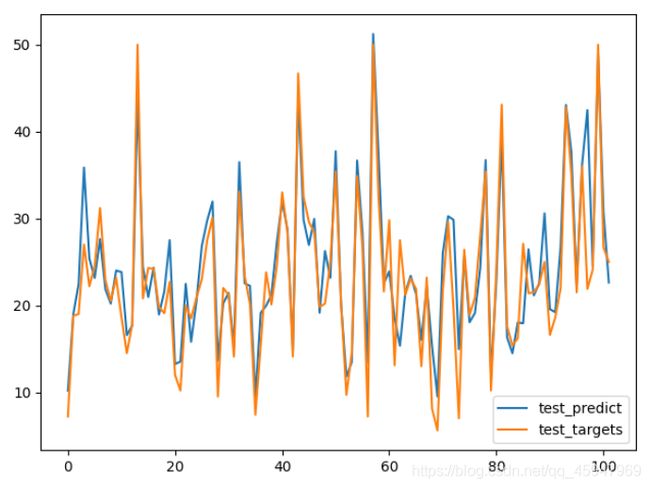
然后评测训练模型，结果如下：

32/102 [========>.....................] - ETA: 0s
102/102 [==============================] - 0s 20us/step
2.789275459214753
[[10.174608]
 [18.987032]
 [22.46014 ]
 [35.86448 ]
 [25.396717]]
[ 7.2 18.8 19.  27.  22.2]

发现效果不是很好，于是重新构建一个网络，如下：

第一层：全连接层，设置64个单元，激活函数为‘relu’

第二层：全连接层，设置64个单元，激活函数为‘relu’

第三层：全连接层，设置32个单元，激活函数为’relu’

第四层：全连接层，设置16个单元，激活函数为’relu’

第五层：全连接层，设置1个单元

model = Sequential([  
Dense(64,activation="relu",input_shape=(13,),name="dense1"),  
Dense(64,activation="relu",name="dense2"),  
Dense(32,activation="relu",name="dense3"),  
Dense(16,activation="relu",name="dense4"),  
Dense(1,name="dense5"),  
])  
model.compile(optimizer="adam",loss="mse",metrics=['mae'])  

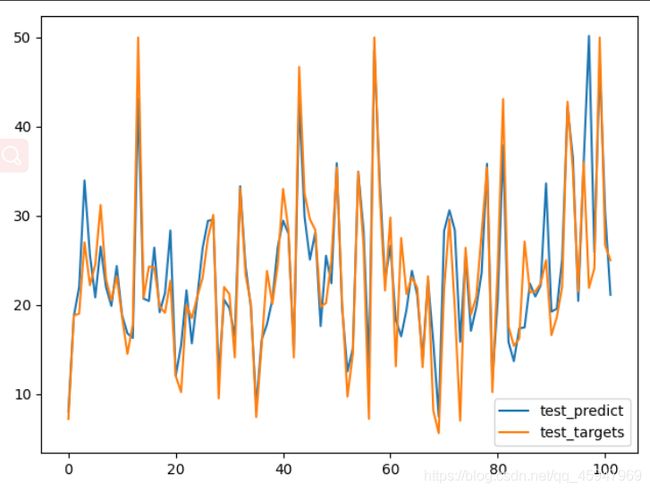
 运行结果如下：

32/102 [========>.....................] - ETA: 0s
102/102 [==============================] - 0s 488us/step
2.761275282093123
[[ 7.9929595]
[18.680035 ]
[22.014114 ]
[33.955776 ]
[25.633823 ]]
[ 7.2 18.8 19.  27.  22.2]

 

运行结果相较与之前三层的模型有所提升，但预测结果还不是特别理想，与引入K折交叉验证的方法，对模型进行改进。一般情况将K折交叉验证用于模型调优，找到使得模型泛化性能最优的超参值。

K折验证的原理：
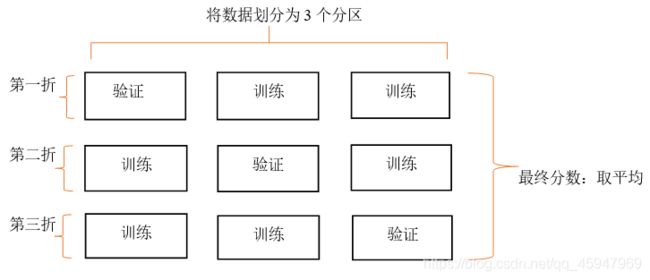
K折验证(k-fold validation)将数据划分为大小相同的K个分区。对于每个分区i，在剩余的K-1个分区上训练模型，然后在分区i上评估模型。最终分数等于K个分数的平均值。对于不同的训练集—测试集划分，如果模型性能的变化很大，那么这种方法很有用。与留出验证一样，这种方法也需要独立的验证集进行模型校正。
K折交叉验证的示意图见图下所示：

 找到后，在全部训练集上重新训练模型，并使用独立测试集对模型性能做出最终评价。K折交叉验证使用了无重复抽样技术的好处：每次迭代过程中每个样本点只有一次被划入训练集或测试集的机会。

K折验证程序：

###K折验证###  
k = 4  
num_val_samples = len(train_data) // k  
num_epochs = 100  
all_scores = []  
for i in range(k):  
    print('processing fold #',i)  
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]  
    val_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]  
  
    partial_train_data = np.concatenate(  
        [train_data[:i*num_val_samples],  
         train_data[(i+1)*num_val_samples:]],  
        axis=0)  
    partial_train_targets = np.concatenate(  
        [train_targets[:i * num_val_samples],  
         train_targets[(i + 1) * num_val_samples:]],  
        axis=0)  
    model = build_model()  
    model.fit(partial_train_data,partial_train_targets,  
              epochs=num_epochs,batch_size=1,verbose=0)  
    val_mse,val_mae = model.evaluate(val_data,val_targets,verbose=0)  
    all_scores.append(val_mae)  
# print(all_scores)  
# print(np.mean(all_scores))  
##保存K折验证的结果  
num_epochs = 40  
all_mae_histories = []  
for i in range(k):  
    print('processing fold #',i)  
    val_data = train_data[i * num_val_samples:(i + 1) * num_val_samples]  
    val_targets = train_targets[i * num_val_samples:(i + 1) * num_val_samples]  
  
    partial_train_data = np.concatenate(  
        [train_data[:i * num_val_samples],  
        axis=0)  
    partial_train_targets = np.concatenate(  
        [train_targets[:i * num_val_samples],  
         train_targets[(i + 1) * num_val_samples:]],  
        axis=0)  
    model = build_model()  
    history = model.fit(partial_train_data, partial_train_targets,  
                        validation_data=(val_data,val_targets),  
                        epochs=num_epochs, batch_size=1, verbose=0)  
    mae_history = history.history['val_mean_absolute_error']  
    all_mae_histories.append(mae_history)  
#计算所有轮次中的K折验证分数平均值  
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]  
###绘制验证分数###  
plt.plot(range(1,len(average_mae_history)+1),average_mae_history)  
plt.xlabel('Epochs')  
plt.ylabel('Validation MAE')  
plt.show()  
###绘制验证分数（删除前10个数据点）###  
def smooth_curve(points,factor=0.9):  
    smoothed_points = []  
    for point in points:  
        if smoothed_points:  
            previous = smoothed_points[-1]  
           smoothed_points.append(previous * factor + point * (1-factor))  
        else:  
            smoothed_points.append(point)  
    return smoothed_points  
smooth_mae_history = smooth_curve(average_mae_history[10:])  
plt.plot(range(1,len(smooth_mae_history)+1),smooth_mae_history)  
plt.xlabel('Epochs')  
plt.ylabel('Validation MAE')  
plt.show()  
l_scores.append(val_mae)  

加入K折交叉验证平均绝对误差在500轮模型的结果：

32/102 [========>.....................] - ETA: 0s
102/102 [==============================] - 0s 4ms/step
3.0198199421751735
[[ 9.111161]
 [19.31696 ]
 [20.284008]
 [27.230476]
 [22.588339]]
[ 7.2 18.8 19.  27.  22.2]

 

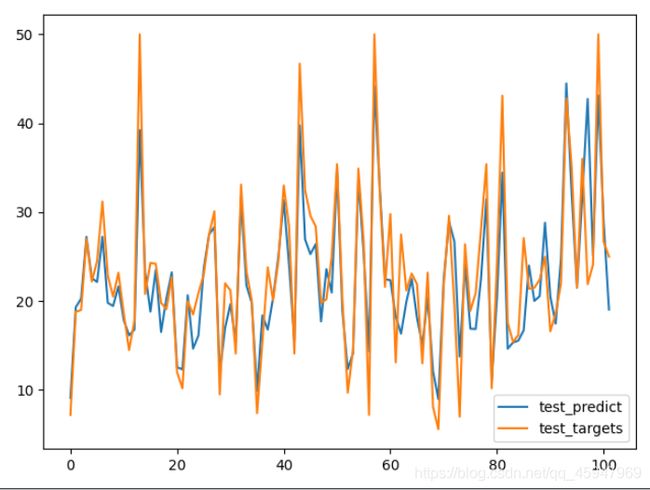
 由上图可知，K折交叉验证轮次在70轮左右就过拟合了，因此我们把K折交叉验证训练轮刚改为80轮，模型的运行结果如下：

 由输出结果可知，预测房价与实际房价相差约2400美元，然后查看前五个预测房屋价格分别是：8.473495，20.397701，22.871258，33.599148，25.75566，与实际房屋价格比较符合。

 

四、总结

1. 回归问题常用的损失函数是均方误差MSE
2. 回归问题常用的评估指标是平均绝对误差MAE
3. 如果输入数据特征具有不同的取值范围，应先进行预处理，对每个特征进行单独缩放
4. 如果可用的数据量很少，可以使用k折验证以可靠地评估模型
5. 如果可用的训练数量很少，模型训练出来的结果不是特别理想，可以适当调节网络层数，或是训练代数。

                                         

五、参考文献

[1][美]弗朗索瓦.肖莱,张亮 译.Python深度学习[M].北京：中国工信出版集团，2018：67-72.

[2]波士顿房价预测Python深度学习，CSDN，https://blog.csdn.net/ /article/details.nonecase

[3]梁子超,李智炜,赖铿,林卓琛,李铁钢,张晋昕.10折交叉验证用于预测模型泛化能力评价及其R软件实现[J].中国医院统计,2020,27(04):289-292.

直接下载课程设计PDF