第二课.图卷积神经网络

卷积神经网络

在计算机视觉中，卷积网络是一种高效的局部特征提取工具，一个卷积层包含多个filter，每个filter的kernel数量等于输入张量的通道数，输出张量的通道数量就是filter的个数，一个filter中的各个kernel是不同的；
可以理解为不同的filter提取不同的局部特征，filter内的kernel不同是为了获取输入张量上不同通道的局部信息，最后加和得到该filter对应的局部特征相似度；

上图的输入张量有3个通道，设置了一个filter，容易理解这个filter应当有3个kernel，通过在输入张量上滑动加和得到输出张量，输出张量为1个通道；通过以上计算可见，卷积神经网络其实相当于不同的全连接网络组成一组滤波器(全连接网络不附带激活函数)，作用在输入张量的局部特征上，这些局部特征计算得到的张量再组合成为新的张量；

计算机视觉任务中，Pooling layer 用于对局部特征求最大或者求平均，比如这是一个MaxPool2d：

补充一个部分，MaxPooling其实相当于一个特殊的注意力机制，只不过注意力完全赋给了局部最大的那个值；

2015年出现了ResNet，后继2017年出现DenseNet（以上内容回顾Pytorch笔记本第八课），ResNet的特征融合是特征的元素相加，残差结构减轻了梯度消失vanishing-gradient问题，同时加强了特征的传递，DenseNet的每层卷积输出都会沿着通道拼接前面所有卷积层的输出特征，进一步减轻梯度消失和加强特征传递，更有效地利用了特征；

现在补充2019年提出的思想CSPNet：Cross Stage Partial Net，CSP的思想是沿着张量的通道维度将部分特征留下，剩余特征用于卷积，在最后把之前留下的那一部分特征（partial）拼接到输出上；

上图(a)是标准的DenseNet，可看到每层卷积输出都拼接了前面卷积的输出张量，最后将输出张量传递到Transition Layer调整通道数，Transition Layer就是一个简单的 $kernelsize=1\times 1$ 卷积层；图(b)是融入了CSP思想的DenseNet，可看出保留了一部分特征在最后拼接到DenseBlock的输出张量上，然后进行Transition操作；
CSP保留部分特征在最后进行拼接，这样做可以适当减少学习负担，让模型更易于在嵌入式设备上部署，另外，原始特征的融合加强了CNN的表达能力；

如果将CNN用于图像分类，对比一下，图神经网络GNN可以进行图分类，比如：人脑的各个区域可以由节点表示，节点之间不同的关系反映大脑的意识传递，不同时刻下，对人脑的图结构进行图分类，就可以获知该大脑想要执行什么动作（action）；

图卷积神经网络

GNN数据集

在了解图卷积神经网络（GCN，Graph Convolution Networks）前，先认识GNN常用的数据集：

• KarateClub：数据为无向图，来源于论文An Information Flow Model for Conflict and Fission in Small Groups
• TUDataset：包括58个基础的分类数据集集合，数据都为无向图，如“IMDB-BINARY”，“PROTEINS”等，来源于TU Dortmund University
• Planetoid：引文网络数据集，包括“Cora”, “CiteSeer” and “PubMed”，数据都为无向图，来源于论文Revisiting Semi-Supervised Learning with Graph Embeddings，节点代表文档，边代表引用关系
• CoraFull：完整的“Cora”引文网络数据集，数据为无向图，来源于论文Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking，节点代表文档，边代表引用关系
• Coauthor：共同作者网络数据集，包括“CS”和“Physics”，数据都为无向图，来源于论文Pitfalls of Graph Neural Network Evaluation。节点代表作者，若是共同作者则被边相连。学习任务是将作者映射到各自的研究领域中
• Amazon：亚马逊网络数据集，包括“Computers”和“Photo”，数据都为无向图，来源于论文Pitfalls of Graph Neural Network Evaluation。节点代表货物，边代表两种货物经常被同时购买。学习任务是将货物映射到各自的种类里
• PPI：蛋白质-蛋白质反应网络，数据为无向图，来源于论文Predicting multicellular function through multilayer tissue networks
• Entities：关系实体网络，包括“AIFB”, “MUTAG”, “BGS” 和“AM”，数据都为无向图，来源于论文Modeling Relational Data with Graph Convolutional Networks
• BitcoinOTC：数据为有向图，包括138个“who-trusts-whom”网络，来源于论文EvolveGCN: Evolving Graph Convolutional Networks for Dynamic Graphs

GNN是一个广泛的概念，GCN是将卷积思想（邻域聚合）引入GNN，GCN常用于在图数据中解决节点分类问题；例如引文网络，只有部分节点具有已知标签，每个节点都有其属性（特征）：

CNN的邻域聚合对象是规则的张量，GCN的处理对象是当前节点以及其周围直接相连的节点，对比卷积网络，一个节点及其周围相连的节点就是整个图中的一个局部特征：

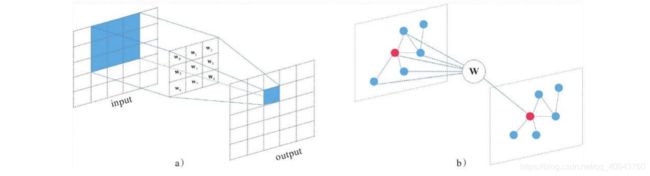
上图(b)中看出，GCN正在处理一个红色节点，先获取到其邻居，然后将这些局部节点的特征融合，进行全连接网络一样的变换（与张量$W$点积），得到当前节点的另一种特征表达，这种表达中包含了该节点的高层语义信息，从而完成节点的分类；

和卷积神经网络一样，GCN也有感受野，比如从一阶邻居节点逐步扩大至二阶邻居节点范围，下图(a)是CNN的感受野变化示意图，图(b)是GCN的感受野变化示意图：

图的表示

图数据不同于图像张量的规则性，每个节点的邻居节点数量是不固定的，所以需要先用固定的数据形态表达图，首先了解邻接列表Adjacency List：

如上图所示，存在一个有向图（无向图也是特殊的有向图），现在记录每个节点指向的邻居节点，从而获得该图的邻接列表，虽然邻接列表可以描述图，但依然不利于使用机器进行计算，所以考虑邻接矩阵Adjacency Matrix；

现存在一个图$G$，共$n$个节点，从$v_1$到$v_n$，定义$A$为该图的邻接矩阵，$A$的形状为$(n,n)$，其元素为$a_{i,j}$，如果存在节点$v_i$指向$v_j$，则记录：$a_{i,j}=1$；否则$a_{i,j}=0$；回顾第一课，无向图的边是无向边，即两个节点是互相指向，因此无向图的邻接矩阵应该关于对角线对称；比如以下两个图，一个是无向图，一个是有向图，其对应的邻接矩阵为：

另外补充度矩阵Degree Matrix，度矩阵是对角阵，对角线上的元素为各个顶点的度，节点$v_i$的度表示和该节点相关联的边的数量，对于有向图，节点$v_i$的度分为节点$v_i$的出度和入度，即从节点$v_i$出去的有向边的数量和进入节点$v_i$的有向边的数量；

对于无向图，节点的度直接记录其关联的边数量，如果一个节点存在自己关联自己情况，关联边数量应该为2，则度为2：

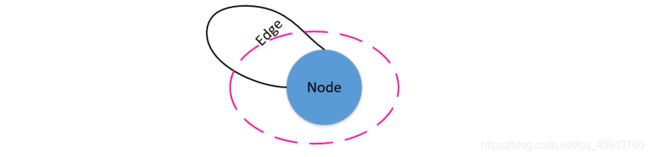
度矩阵记为$D$，形状同样是$(n,n)$，其对角线才有值$d_{i,i}=deg(v_i)$，其他位置值为0；比如以下无向图和其对应的度矩阵：

GCN

为了在图数据上进行类似卷积一样的局部信息聚合，最简单的方式是：
$$Z=\sigma (AXW+b)$$
图$G$有$n$个节点，$X$是所有节点特征组成的张量（$n,c$），$c$是每个节点的特征维数，$A$是图的邻接矩阵（$n,n$），$W,b$是待学习的参数，参数$W$的形状为$(c,h)$，$h$代表变换后输出特征的维数，经过$\sigma$非线性变换得到各个节点组合的输出张量$Z$，$Z$的形状为$(n,h)$，通常$Z$具有高层语义信息；

考虑以下图数据：

直接使用邻接矩阵$A$与特征张量$X$表达为$AX$，其形状为$(n,c)=(5,3)$，$AX$代表了融合图结构后的特征信息，第1行第1列的值由邻接矩阵第1行与特征矩阵第1列点积得到，同理，第1行第2列的值由邻接矩阵第1行与特征矩阵第2列点积得到，可见$AX$的第1行为节点A的邻居（节点E）的特征信息，$AX$的第2行为节点B的邻居（节点E和节点D融合）的特征信息，后面的数据同理；

使用张量$W$对$AX$进行线性变换，由于$AX$的每一行已经存储了节点的邻域信息，所以$AXW$相当于在对局部信息进行操作，即实现了卷积的思想；

但当前的表达$AX$存在问题，对于无自关联的节点，邻接矩阵的对角线值为0，于是$AX$会丢失当前节点自身的特征信息，只剩下其邻居节点的特征信息；为了解决这个问题，对邻接矩阵进行操作：
$$A=A+\lambda I$$
通常令$\lambda =1$，由于单位矩阵对角线值为1，其余值为0，与邻接矩阵相加后正好弥补了节点自身信息丢失的问题，系数$\lambda$决定了节点自身信息的重要程度；

当使用$A$时，改变了图间节点的关系，所以根据新的图更新度矩阵$D$，此处虽然节点自关联，度的增量可以是2，也可以是1，更新后的度矩阵记为$D$：

使用到度矩阵是为了对数据的尺度进行缩放，可以表达为：
$$D^{-1}AX$$
$A$的第 $i$ 行将会被$D^{-1}$的元素${d^{-1}}_{i,i}$缩放，度矩阵体现了节点被其他节点的关联程度，一个节点与其他节点的关联程度越强，度数越大，信息融合的值越大，通过值大小与之成反比的$D^{-1}$，计算$D^{-1}AX$时，可以平衡节点之间的特征尺度，从而得到数据尺度相差不大的特征矩阵，更有利于神经网络学习；

上面的形式$D^{-1}AX$中，$D^{-1}$只缩放了$A$的行，忽略了缩放$A$的列，直观地，可以改成：
$$D^{-1}A{D}^{-1}X$$
这样之后，低度的节点将会对邻居产生相对更多的影响，高度的节点在众多邻居上分散影响，降低了对某个具体邻居的影响；以上过程相当于对$A$进行了两次缩放，一次对行进行，一次对列进行，为了将其缩放至一个合适的程度，改成：
$$D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}X$$
记$A=D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$，由此可以得到一层图卷积神经网络：
$$Z=\sigma (AXW+b)=\sigma (D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}XW+b)$$

• 其中，$D^{-\frac{1}{2}}$和$A$的形状均为$(n,n)$；
• $X$是所有节点特征组成的张量，形状为$(n,c)$，$c$是每个节点的特征维数；
• 参数$W$的形状为$(c,h)$，$h$代表变换后输出特征的维数；
• 经过$\sigma$非线性变换得到各个节点组合的输出张量$Z$，$Z$的形状为$(n,h)$，$Z$具有高层语义信息；

直观地，图卷积神经网络的层数也可以加深，比如加深至两层，令$W^{(1)}$形状为$(c,h)$，$W^{(2)}$形状为$(h,f)$，假设节点的类别数为$f$：
$$Z=softmax(A[ReLU(AX{W}^{(1)}+b^{(1)})]W^{(2)}+b^{(2)})$$
节点的分类可以使用交叉熵计算损失：
$$loss=-\sum _{l\in Y_L}\sum _{i=1}^{f}targe{t}_{l,i}log(Z_{l,i})$$

• 其中，$Y_L$代表所有具有已知类别（标签）的节点，图数据的节点共有$f$类；
• $targe{t}_{l,i}$即代表$Y_L$中第$l$个节点，其类别为第$i$类；
• $Z_{l,i}$即图神经网络的输出，反映了预测$Y_L$中第$l$个节点，并且其类别为第$i$类的概率

GNN的基准化：Benchmarking Graph Neural Networks

GNN模型广泛，但缺乏一个标准的基准，以及在大型数据集上开展的一致性实验，Benchmarking Graph Neural Networks 一文在GNN的基准化上做出了贡献，作者提出了可重现的GNN基准框架，并为研究人员提供了方法以便利地添加新的数据集和模型，地址：Benchmarking Graph Neural Networks

基准框架可以应用于数学中的新型中等规模图形数据集建模，可在计算机视觉，化学，组合优化等问题上设计有效的图神经网络；实现了图卷积，各向异性扩散，残差连接和归一化等层，这些层是开发健壮且可扩展的GNN通用构建模块