Pytorch实现RNN循环神经网络（实例）以及比较不同优化器对应的loss曲线

最近在b站上学习了几个关于pytorch框架视频，特地做了下笔记。

一、线性回归

最简单的一个线性回归问题，拟合一个二次函数，代码很简单，就不赘述了，直接贴上代码：

import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt


x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # 加入噪声

x, y = Variable(x), Variable(y)

# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()
# print(x)
# print(x.data)
# print(x.numpy())
# print(x.data.numpy())


class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.relu(self.hidden(x))
        x = self.predict(x)
        return x


net = Net(1, 10, 1)

plt.ion()  # something about plotting
plt.show()

optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
loss_func = torch.nn.MSELoss()


for t in range(100):
    prediction = net(x)
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'loss=%.4f' % loss.item(), fontdict={
     'size': 20, 'color': 'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()

产生的结果如下（实际上输出是个动态图，我保存的是静态图）：

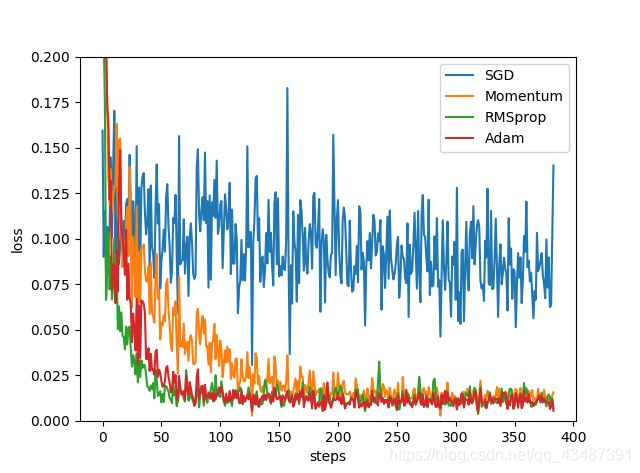
二、比较SGD、Momentum、RMSprop、Adam差异

还是利用上述二次函数的例子，使用SGD、Momentum、RMSprop、Adam优化器算法对模型优化，比较各个优化器产生的loss曲线。
首先简单介绍一下这四种梯度下降算法：

SGD

随机梯度下降 (Stochastic Gradient Descent)：是最基础的神经网络梯度算法
SGD 参数更新的算法 :

p=p−lr∗g 

Momentum SGD

Momentum SGD是基于动量的算法
Momentum SGD 参数更新的算法 :

v=m∗v+g
p=p−lr∗v 

其中 p, g, v 和 m 分别表示参数, 梯度, 速度和动量

RMSprop

root mean square prop是一种自适应学习率的算法

Adam

Adam （ Adaptive Moment Estimate）, Adam算法结合了基于动量的算法和基于自适应学习率的算法
Adam 算法记录了梯度的一阶矩 (梯度的期望值) 和二阶矩 (梯度平方的期望值)

我之前看到一篇很详细的帖子介绍这四种算法，附上链接：点这里

下面给出代码：

import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt


# hyper parameters
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size())) # 加入噪声

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2)


# default network
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)  # hidden layer
        self.predict = torch.nn.Linear(20, 1)  # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))  # activation function for hidden layer
        x = self.predict(x)  # linear output
        return x


# different nets
def main():
    net_SGD = Net()
    net_Momentum = Net()
    net_RMSprop = Net()
    net_Adam = Net()
    nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

    opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
    opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
    opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
    opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
    optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

    loss_func = torch.nn.MSELoss()
    losses_his = [[], [], [], []]

    for epoch in range(EPOCH):
        print(epoch)
        for step, (batch_x, batch_y) in enumerate(loader):
            # b_x = Variable(batch_x)
            # b_y = Variable(batch_y)

            for net, opt, l_his in zip(nets, optimizers, losses_his):
                output = net(batch_x)
                loss = loss_func(output, batch_y)
                opt.zero_grad()
                loss.backward()
                opt.step()
                l_his.append(loss.item())

    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his in enumerate(losses_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('steps')
    plt.ylabel('loss')
    plt.ylim((0, 0.2))
    plt.show()


if __name__ == '__main__':
    main()

运行一下就可以得到这四种梯度下降算法输出的loss曲线：

三、实现RNN循环神经网络

循环神经网络（Recurrent Neural Network, RNN）是一类以序列数据为输入，在序列的演进方向进行递归且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network）；也就是说它可以理解为具有‘记忆’功能，具有参数共享功能。
下面用RNN实现sin函数去拟合cos函数的实例：

import torch
from torch import nn
# import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
import numpy as np

torch.manual_seed(1)  # reproducible

# Hyper Parameters
TIME_STEP = 10  # rnn time step
INPUT_SIZE = 1  # rnn input size
LR = 0.02  # learning rate


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()
        self.rnn = nn.RNN(
            input_size=INPUT_SIZE,
            hidden_size=32,
            num_layers=1,
            batch_first=True
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h_state):

        # x (batch, time_step, input_size)
        # h_state (n_layers, batch, hidden_size)
        # r_out (batch, time_step, hidden_size)
        r_out, h_state = self.rnn(x, h_state)
        outs = []
        for time_step in range(r_out.size(1)):
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state


rnn = RNN()
# print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)  # optimize all cnn parameters
loss_func = nn.MSELoss()
h_state = None

plt.figure(1, figsize=(12, 5))
plt.ion()

for step in range(120):
    start, end = step * np.pi, (step + 1)*np.pi  # time steps
    # use sin predicts cos
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32)
    x_np = np.sin(steps)
    y_np = np.cos(steps)

    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])  # shape (batch, time_step, input_size)
    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])

    prediction, h_state = rnn(x, h_state)
    # print(h_state)
    h_state = h_state.data 
    # print(h_state)

    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    plt.plot(steps, y_np.flatten(), 'r-')
    plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
    plt.draw()
    plt.pause(0.05)

plt.ioff()
plt.show()

注意代码中有一行

h_state = h_state.data

是为了去除h_state中最后一个元素 grad_fn=，使其又可以输入到下一次循环中

最后给出我们的输出结果：