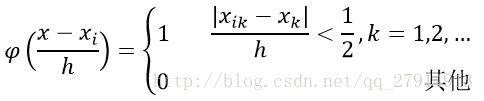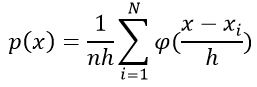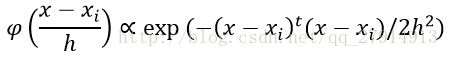parzen窗方法和k近邻方法估计概率密度

机器学习实验四，详情请参考《模式分类》第二版第四章课后上机练习4.3、4.4节

实验环境：

Matlab2016a

Parzen窗估计方法：

已知测试样本数据x1,x2,…,xn，在不利用有关数据分布的先验知识，对数据分布不附加任何假定的前提下，假设R是以x为中心的超立方体，h为这个超立方体的边长，对于二维情况，方形中有面积V=h^2，在三维情况中立方体体积V=h^3。
根据以下公式，表示x是否落入超立方体区域中：

估计它的概率分布：

其中n为样本数量，h为选择的窗的长度，φ(.)为核函数，通常采用矩形窗和高斯窗。

k-近邻估计方法：

在Parzen算法中，窗函数的选择往往是个需要权衡的问题，k-最近邻算法提供了一种解决方法，是另一种非常经典的非参数估计法。基本思路是：已知训练样本数据x1,x2,…,xn而估计p(x)，以点x为中心，不断扩大体积Vn，直到区域内包含k个样本点为止，其中k是关于n的某一个特定函数，这些样本被称为点x的k个最近邻点。

当涉及到邻点时，通常需要计算观测点间的距离或其他的相似性度量，这些度量能够根据自变量得出。这里我们选用最常见的距离度量方法：欧几里德距离。

最简单的情况是当k=1的情况，这时我们发现观测点就是最近的（最近邻）。一个显著的事实是：这是简单的、直观的、有力的分类方法，尤其当我们的训练集中观测点的数目n很大的时候。可以证明，k最近邻估计的误分概率不高于当知道每个类的精确概率密度函数时误分概率的两倍。

实验内容：

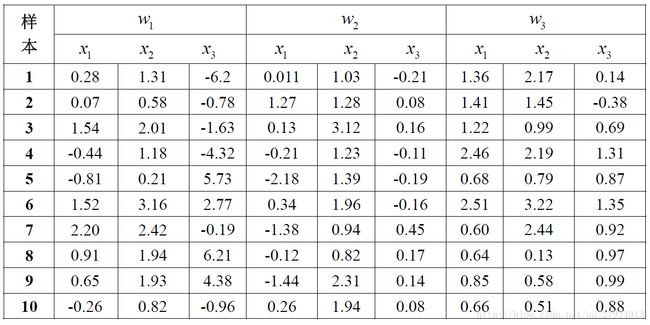
给定以下三个类别的三维数据：

（1）使用parzen窗估计方法，窗函数为一个球形高斯函数：

（a）编写程序，使用parzen窗方法对一个任意的测试样本点进行分类，对分类器的训练使用表格中的三维数据。令h=1，对（0.5，0.1，0.0），（0.31，1.51，-0.50），（-0.3，0.44，-0.1）进行分类。
（b）令h=0.1，重复a。

实验步骤：

根据parzen窗的概率密度估计公式，编写parzen窗函数，输入三个参数，分别为三维数据w、参数h、测试点x，输出测试点在三个类别中估计的概率密度：

function r=parzen(w,h,x)
[rows,~,dimension]=size(w);
r=zeros(1,dimension);
for i=1:dimension
    hn=h;
    for j=1:rows
        hn=hn/sqrt(j);
        r(i)=r(i)+exp(-(x-w(j,:,i))*(x-w(j,:,i))'/(2*power(hn,2)))/(sqrt(2*3.14)*hn);
    end
    r(i)=r(i)/rows;
End

求出测试点在三个类别中的概率密度后，哪个概率密度大说明测试点属于哪个类别的概率大。find函数找出最大的概率密度，输出测试点的类别：

h=1;
for i=1:3
    r=parzen(w,h,x(i,:));
    result=find(r==max(r));
    X=['点[',num2str(x(i,:)),']落在三个类别的概率分别为：',num2str(r)];
    Y=['因此，点[',num2str(x(i,:)),']落在第',num2str(result),'类'];
    disp(X);disp(Y);disp(' ');
end

程序运行的结果如下：

当h=0.1时，同样得到结果如下：

（2）使用k近邻概率密度估计方法。
（a）编写程序，对于一维的情况，当有n个数据样本点时，进行k近邻概率密度估计。对于类别w3中的特征x1，画出k=1，3，5时的概率密度估计结果。
（b）编写程序，对于二维的情况，当有n个数据样本点时，进行k近邻概率密度估计。对于类别w2中的特征（x1，x2），画出k=1，3，5时的概率密度估计结果。
（c）编写程序，对于三维的情况，当有n个数据样本点时，进行k近邻概率密度估计。对点（-0.41，0.82，0.88），（0.14，0.72，4.1），（-0.81，0.61，-0.38）进行估计。

实验步骤：

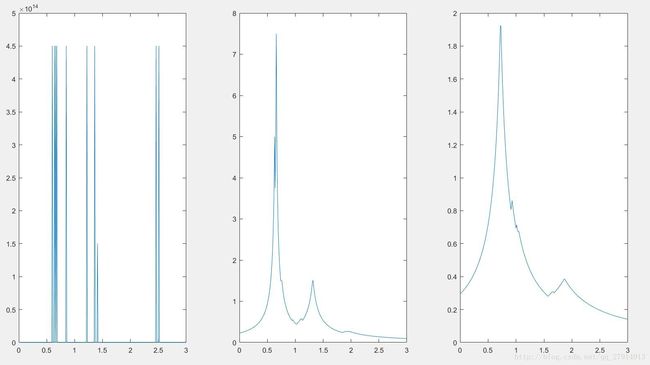
根据式子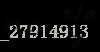：，k取不同值使V的值随之改变，一维情况下，样本点相当于分布在一条线上，V的值就等于样本点到它第k近邻的距离的两倍。概率密度画出来是二维的曲线。观察样本点的范围，以（0.01:0.01:3）取样300个点作为x轴，求出每个点的概率密度后作为y轴，即可画出概率密度曲线。需要注意的是，k=1时，求这300个点与10个样本点的最近距离时，很明显会有10个点求出的V为0，为了避免0作为除数，编程时，V可以加上eps（k=3，5时不存在V=0）：

load sample_ex4.mat;
x1=w(:,1,3);
[rows,cols]=size(x1);
p=zeros(1,300);
sample=(0.01:0.01:3);
dist=zeros(300,rows);
for i=1:1:300
    for j=1:rows
        dist(i,j)=abs(sample(i)-x1(j,1));
    end
end
dist_sort=sort(dist,2); %按行排序
for k=1:2:5
    for i=1:300 
            p(i)=k/rows/(2*dist_sort(i,k)+eps); %避免除于0的情况
    end
    if(k==1)
        subplot(131);
        plot(sample,p);
    elseif(k==3)
        subplot(132);
        plot(sample,p);
    elseif(k==5)
        subplot(133);
        plot(sample,p);
    end
End

画出概率密度曲线如下：

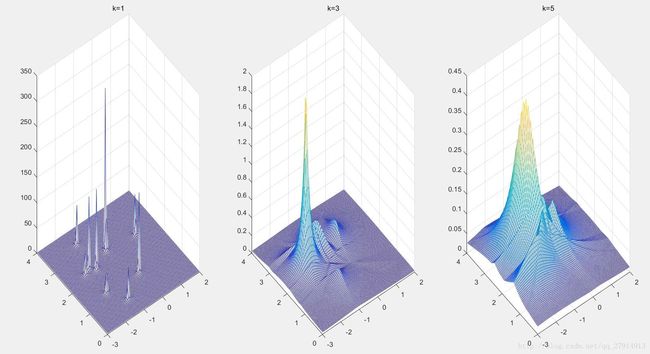
可以看出，k从1到5，曲线尖峰减少，曲线变平滑。对于二维情况，同样是使用公式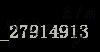，不过V在二维情况下对应的是一个圆的面积pi*r2。观察样本点的波动范围，可以(-2.95:0.05:2)每隔0.05取样100个点作为x轴，以(0.04:0.04:4)每隔0.04取样100个点作为y轴，需要求出这100*100个点的概率密度，画出为一个三维图像。由于此处不会出现V=0的情况，因此不需加eps。画出的结果如下：

K增大，同样可以看出曲面变得平滑。对于第三问，给出了测试点，需要求出测试点在三个类别中的概率密度。此时的V就是球体的体积。

load sample_ex4.mat;
x=[-0.41,0.82,0.88;0.14,0.72,4.1;-0.81,0.61,-0.38];
dist=zeros(3,10,3);
for i=1:3
    for j=1:3
        for k=1:10
            dist(j,k,i)=norm(x(i,:)-w(k,:,j));
        end
    end
end
dist_sort=sort(dist,2);
k=3;
p=zeros(3,3);
for i=1:3
    for j=1:3
        p(i,j)=k/10/(4*3.14*dist_sort(j,k,i)^3/3);
    end
end
for i=1:3
     X=['点 [',num2str(x(i,:)),'] 在三个类别的概率密度分别为：',num2str(p(i,:))];
     disp(X);
end

结果如下：

总结：

Parzen窗和K近邻是非参数估计的两种经典方法。由式子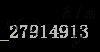，n是已知的总的样本点，k和v未知，parzen窗方法通过固定V而改变k来求概率密度，而k近邻通过固定k改变V来估计概率密度，parzen窗需要先确定条件概率密度后才能对测试点进行分类，而k近邻可以直接根据k个近邻中哪个类别的样本点最多就将其分为哪一类，k近邻模型几乎没有进行什么学习，来一个测试点都要重新计算，并且训练集需要保留，属于lazy-learning。