【数据结构】最全排序汇总 | 考研重点!
本文主要内容
1. 排序及其相关概念的介绍
2. 常见排序及其算法实现
3. 排序算法复杂度及稳定性分析
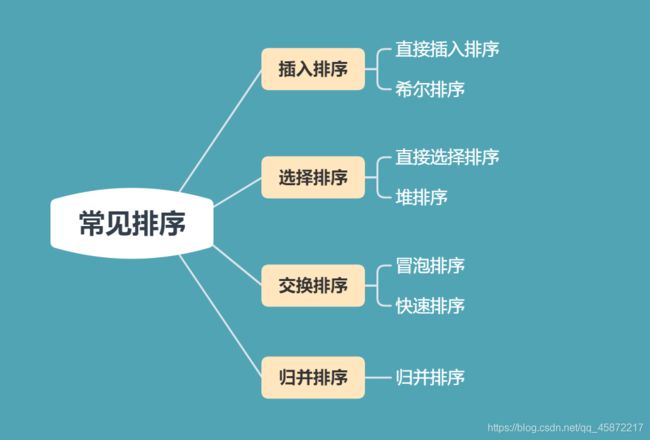
目录
- 本文主要内容
- 一、排序及其相关概念的介绍
- 二、常见排序及其算法实现
-
- 1.插入排序
-
-
- 1.1直接插入排序
- 1.2希尔排序(缩小增量排序)
-
- 2.选择排序
-
-
- 2.1直接选择排序
- 2.1堆排序
-
- 3.交换排序
-
-
- 3.1冒泡排序
- 3.2快速排序
-
- 3.2.1快速排序之左右指针法
- 3.2.2快速排序之挖坑法
- 3.2.3快速排序之前后指针法
- 3.2.4快速排序之非递归实现
-
- 4.归并排序
-
-
- 4.1归并排序
- 4.2归并排序(非递归)
-
- 三、 排序算法复杂度及稳定性分析
一、排序及其相关概念的介绍
- 排序:使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。(即在一个序列中,相同关键字的相对次序在排序前后不发生改变,就称该排序稳定,反之不稳定。)
- 内部排序:数据元素全部放在内存中的排序。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
二、常见排序及其算法实现
1.插入排序
1.1直接插入排序
基本思想:当插入第i(i>=1)个元素时,前面的a[0],a[1],…,a[i-1]已经排好序,此时用a[i]的排序码与a[i-1],a[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。

void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
//把end+1的数据插入到[0,end]的有序区间
int end = i;//end为已经排好的序列的最后的位置
int temp = a[end + 1];//待插入的数据
while (end >= 0)
{
if (temp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = temp;
}
}
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高;反之,越接近逆序,越坏。
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
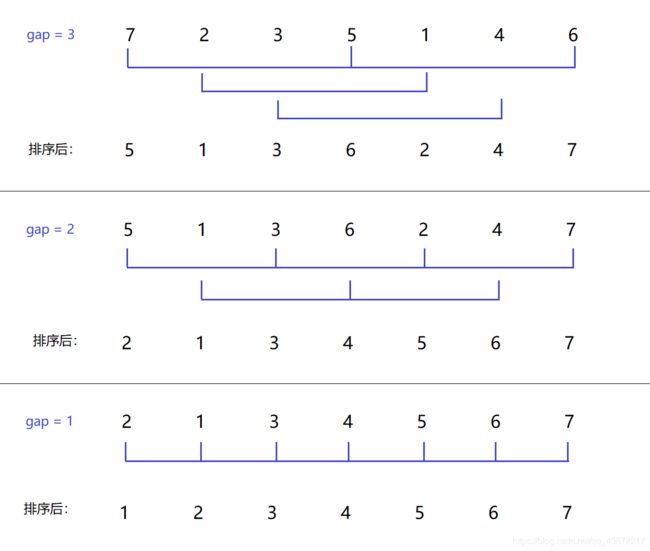
1.2希尔排序(缩小增量排序)
基本思想:先进行预排序,把间距为gap的值分为一组,对每组进行插入排序。再对gap进行递减取值,重复上述分组和排序的工作。当gap=1时,所有记录在统一组内排好序(此时也就是进行直接插入排序)
void ShellSort(int* a, int n)
{
//把gap设置的大一点,然后预排序,让数组接近有序
//最后gap==1,直接插入排序,保证有序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;//gap一直是递减的形态;
//+1 :保证最后一次gap一定是1,才能实现完全排序
for (int i = 0; i < n - gap; i++) // i++实现多组并排
{
//for循环内部是单组内部的排序
int end = i;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;
}
}
}
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap = 1时,数组已经接近有序的了,这样就会很快。整体而言,可以达到优化的效果。
- 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3— N^2)
- 稳定性:不稳定
2.选择排序
2.1直接选择排序
基本思想:在元素集合a[i]–a[n-1]中选择关键码最大(小)的数据元素,若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。在剩余的a[i]–a[n-2](a[i+1]–a[n-1])集合中,重复上述步骤,直到集合剩余1个元素,排序结束。

void SelectSort(int* a, int n)
{
for(int i=1;i<=n-1;i++)//进行n-1趟选择
{
int index=i;
for(int j=i+1;j<=n;j++)//从无序中选取最小,并记录下标
{
if(a[index]>a[j])
index=j;
}
if(index!=i)
swap(a[i],a[index]);
}
}
直接选择排序的特性总结:
- 直接选择排序效率不佳,实际中很少使用。
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.1堆排序
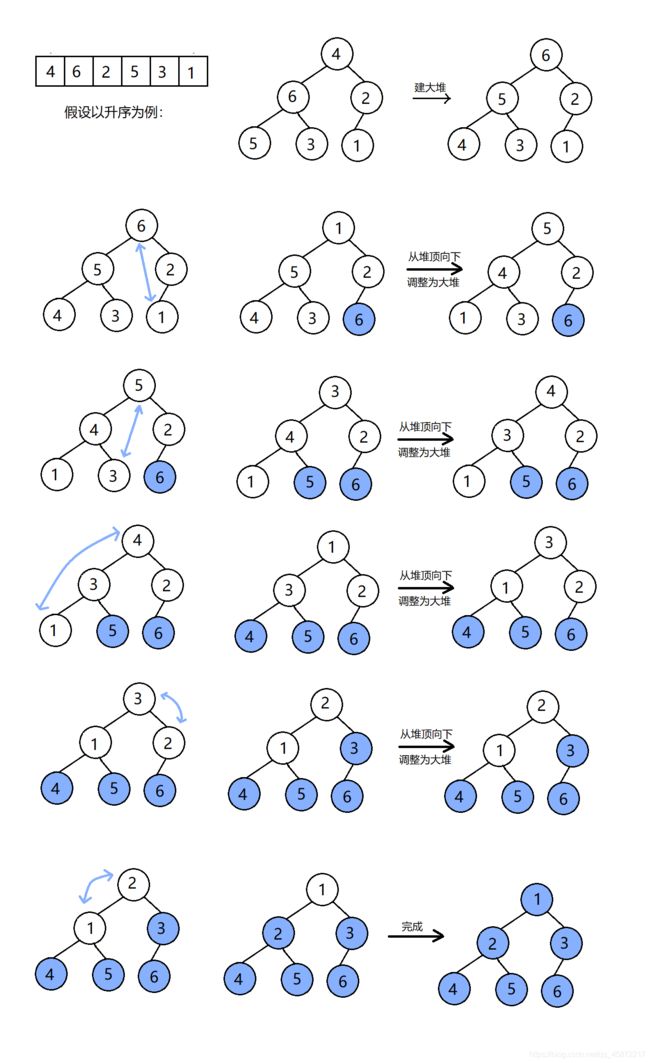
基本思想:利用堆积树(堆)这种数据结构所设计的一种排序算法,通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n&&a[child + 1] > a[child])
{
child++;
}
if (a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//排升序,建大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
end--;
}
}
堆排序的特性总结:
- 堆排序使用堆来选数,效率高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
3.交换排序
3.1冒泡排序
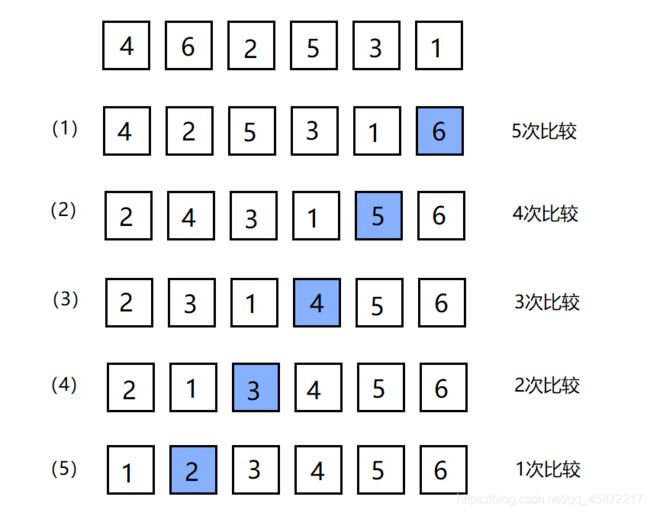
基本思想:对所有相邻记录的关键字值进行比效,如果是逆序,则将其交换,最终达到有序的过程。
void BubbleSort(int* a, int n)
{
int end = n;
while (end > 0)
{
int exchange = 0;
for (int i = 1; i < end; i++)
{
if (a[i - 1]>a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
end--;
}
}
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
3.2快速排序
基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码,将待排序集合分割成两子序列:左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
将区间按照基准值划分为左右两半部分的常见方式有:
1. 左右指针法(hoare版本)
2. 挖坑法
3. 前后指针法
3.2.1快速排序之左右指针法
基本思想:选列表中的一个元素作为基准值,begin指针在第一位找比 它大的值,end指针在最后一位找比它小的值。最终通过一系列的交换,达到基准值的左侧都比它小,右侧都比它大。
注意:若基准值key选择左边第一位,那么要让end先走,这样能保证它们相遇的位置是比key小的位置;若选择右边第一位,那么让begin先走,这样能保证它们相遇的位置是比key大的位置(begin找到大的停下来,然后end去和它相遇)。
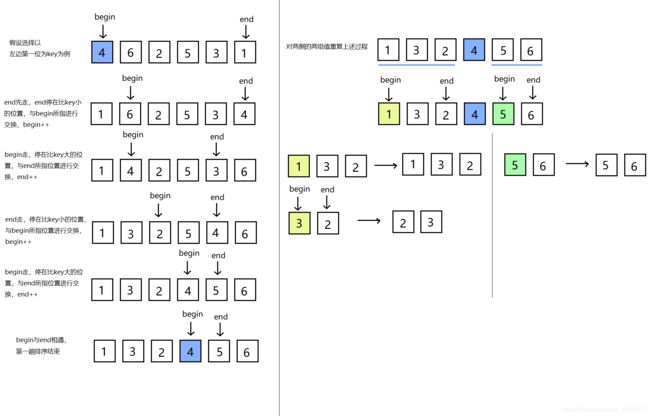
int QuickSort(int* a, int begin, int end)
{
int key = a[end];
int keyindex = end;
while (begin < end)
{
//begin找大
while (begin < end && a[begin] <= key)
{
begin++;
}
//end找小
while (begin < end && a[end] >= key)
{
end--;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[begin], &a[keyindex]);
int div = begin;//相遇的位置
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
3.2.2快速排序之挖坑法
基本思想:选取序列中第一个元素为坑,保存在key中。坑的意思是,这个位置的值被拿走了,可以覆盖,填新的值。那么end先走,找比key的值小的数,填到坑中,end为新的坑。然后begin再走,找比key大的值填入新坑中。直至begin与end相遇结束该趟循环。
挖坑法与左右指针很类似,因此,参照上图即可。
int QuickSort(int* a, int begin, int end)
{
int key = a[end];//坑 (这个位置的值被拿走了,可以覆盖,填新的值)
while (begin < end)
{
while (begin < end&&a[begin] <= key)
{
begin++;
}
//左边找到比key大的填到右边的坑,然后begin位置就形成了新的坑
a[end] = a[begin];
while (begin < end&&a[end] >= key)
{
end--;
}
//右边找到比key小的值填到左边的坑,然后end的位置形成新的坑
a[begin] = a[end];
}
//填一下坑 也就是end和begin相遇的位置
a[begin] = key;
int div = begin;//相遇的位置
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
3.2.3快速排序之前后指针法
基本思想:设置两个指针,分别为prev与cur,prev在cur的前面。选取最后一个元素为基准值,保存至key中。 cur找到比key小的值停下,然后prev++,cur和prev位置的值进行交换。
int PartSort3(int* a, int begin, int end)
{
//cur找到比key小的停下,然后prev++;
//然后cur和prev位置的值交换
int prev = begin - 1;
int cur = begin;
int keyIndex = end;
while (cur < end)
{
if (a[cur] < a[keyIndex] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;
}
Swap(&a[++prev], &a[keyIndex]);
int div = prev;
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
快速排序的特性总结:
- 整体的综合性能和使用场景都比较好
- 时间复杂度分析:
最好的情况:恰巧每次都选到了中位数作为key,那么时间复杂度为O(N*logN)
最坏的情况:key为数组中最大或最小的那个数,时间复杂度O(N^2) 有序的情况下。
*做出“三数取中”改进,所以不会出现最坏的情况,所以时间复杂度不考虑最坏,因此为O(N logN)。 - 空间复杂度:O(logN)
- 稳定性:不稳定
快速排序递归方式的优化:
(1)三数取中法选key:不要选到最大或最小的那个数
int getMidIndex(int *a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return end;
}
else return begin;
}
else //a[begin] > a[mid]
{
if (a[mid]>a[end])
{
return mid;
}
else if (a[begin] > a[end])
{
return end;
}
else return begin;
}
}
(2) 小区间优化:递归到小的子区间(如10个元素以下)时,可以考虑使用插入排序,可以减少整体的递归次数。
3.2.4快速排序之非递归实现
基本思想:将区间划分成若干个子区间,利用栈的性质,来实现每个区间的有序。
void QuickSortNonR(int* a, int left, int right)
{
//用栈来实现
stack st;
stackInit(&st);
stackPush(&st, right);
stackPush(&st, left);
while (!stackEmpty(&st))
{
int begin = stackTop(&st);
stackPop(&st);
int end = stackTop(&st);
stackPop(&st);
//取出栈中的区间[begin,end],开始分
int div = QuickSort(a, begin, end);
//[begin, div-1] div [div+1, end]
if (div + 1 < end) //说明该区间中至少有两个值
{
stackPush(&st, end);
stackPush(&st, div + 1);
}
if (begin < div - 1)
{
stackPush(&st, div - 1);
stackPush(&st, begin);
}
}
stackDestory(&st);
}
4.归并排序
4.1归并排序
基本思想:采用分治法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
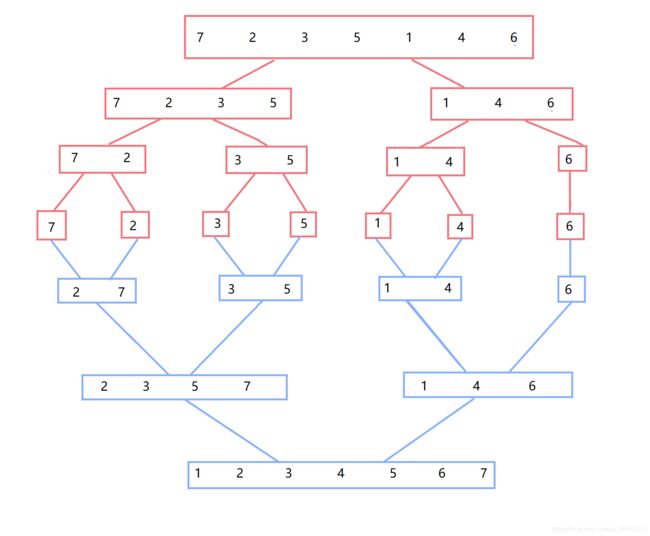
void MergeArr(int* a, int begin1, int end1, int begin2, int end2, int* temp)
{
int left = begin1, right = end2;
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
temp[index++] = a[begin1++];
else
temp[index++] = a[begin2++];
}
while (begin1 <= end1)
temp[index++] = a[begin1++];
while (begin2 <= end2)
temp[index++] = a[begin2++];
// 把归并好的再tmp的数据在拷贝回到原数组
for (int i = left; i <= right; ++i)
a[i] = temp[i];
}
void _MergeSort(int* a, int left, int right, int* temp)
{
if (left>=right)
{
return;
}
int mid = (left + right) / 2;
//[left,mid] [mid+1,right] 有序,则可以合并,现在它们没有序,子问题解决
_MergeSort(a, left, mid, temp);
_MergeSort(a, mid + 1, right, temp);
//归并[left,mid][mid+1,right]有序
MergeArr(a, left, mid, mid + 1, right, temp);
}
// 归并排序递归实现
void MergeSort(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int)*n);
_MergeSort(a, 0, n - 1, temp);
free(temp);
}
归并排序的特性总结:
- 它思考更多的是,解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N) (缺点)
- 稳定性:稳定
4.2归并排序(非递归)
void MergeSortNonR(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int)*n);
int gap = 1;//间隔
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i,i+gap)[i+gap,i+2*gap)
//[i,i+gap-1][i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//会有越界的情况
//1、合并时只有第一组,第二组不存在,就不需要合并
if (begin2 >= n)
{
break;
}
//2、合并时第二组只有部分数据,需要修正end2边界
if (end2 >= n)
{
end2 = n - 1;
}
MergeArr(a, begin1, end1, begin2, end2, temp);
}
gap *= 2;
}
free(temp);
}