FINN CNV二值网络论文

一种快速，可扩展的二值化神经网络框架
2016 FINN: A Framework for Fast, Scalable Binarized Neural Network Inference

1 Abstract

FINN，一个使用灵活的异构流结构构建的快速和灵活的FPGA加速器的框架。实现了全连接、卷积和池化层，每层计算资源可以根据用户提供的吞吐量要求进行调整。在ZC706嵌入式FPGA平台上，系统功耗低于25 W，MNISTdataset上达到每秒1230万个图像分类，延迟为0.31μs，准确率为95.8％，而CIFAR-10和SVHN数据集上的延迟为283μs，21906个图像分类，精度分别为80.1％和94.9％。我们是迄今为止在这些基准测试中报告的最快的分类。

2 Introduction

Alex Net每张图像需要244 MB的参数和14亿浮点操作（1.4 GFLOP），而VGG- 16需要552MB参数和每张图像30.8 GFLOP。使用浮点参数包含了明显的冗余。FPGA在二进制运算中具有更高的理论峰值性能，小内存占用通过将参数保持在芯片上来消除了芯片存储瓶颈，有可能在FPGA上获得性能每秒钟可进行一万亿次（10^12）操作(teraoperations
per second TOPS))。

• 使用roofline模型量化BNNs达到在FPGA上的峰值性能。

• 利用优化将BNN更加高效的映射到FPGA上。

• BNN架构和加速器构建工具，允许定制吞吐量。

• 一系列原型展示了BNNs在现成的FPGA平台上的潜力。

2.2 BNN

我们从三个方面考虑神经网络层的二值化：二进制输入激活，二进制突触权重和二进制输出激活。 如果这三部分都是二进制的，我们将其称为完全二值化，将具有一个或两个部分是二进制的情况称为部分二值化。

XNOR-Net在ImageNet数据集上得出完全二值化高达51.2%的和部分二值化65.5%的Top-1精度。
DoReFa-Net探讨了前向传递和后向传递期间精确度的降低，这打开了在FPGA上训练神经网络的可能性。 ImageNet top-1准确度为：完全二值化43％，部分二值化53％。

2.3 硬件部署

在FPGA和ASIC上，映射将神经网络到硬件的架构主要有：
1）单个处理器，通常采用脉动阵列的形式，按照顺序处理每一层;（参考论文8）
2）流式架构，由每个网络层一个处理引擎组成; （参考论文9）
3）矢量处理器，其指令专用于加速卷积的基元运算;（参考论文10）
4）神经突触处理器，它实现了许多数字神经元及其互连权重。（参考论文11）

1）Zhang描述了一个单处理引擎风格的体系结构，使用theoretical roofline models tool来设计加速器，来优化每个层的执行运算。
2）同步数据流（SDF）模型
3）一种RISC-V矢量处理器，具有针对CNN的特定宏指令，包括2D卷积，2D空间池，点积和元素非线性映射函数
4）TrueNorth （参考论文11）是一种低功率、并行ASIC， 内部路由器可以将任何内核上的任何输入连接到任何内核上的任何神经元，从而允许在固定硬件上实现许多网络拓扑。

3 BNN在FPGA上的准确性和峰值性能

3.1 使用Roofline估算性能

为了估计和比较BNN性能与固定点CNN，我们使用了一个roofline模型[29]，它考虑了存储器带宽，峰值计算性能和算术强度（读取或写入的off-chip存储器的每个字节执行的数学运算的数量）。 对于特定算术强度，roofline曲线与垂直线的交点给出理论峰值性能点，其可以是计算约束，也可以是存储器约束。

FPGA的二进制运算的计算限制性能为66 TOPS，比8位高出约16倍，与16位固定点操作相比高出53倍。由于二值化的AlexNet仅需要7.4 MB的参数（与8位的50 MB相比），整个神经网络模型可以保存在片上存储器中，二值化和8位固定点AlexNet变体的算术强度用垂直线表示，因此，BNN几乎能够达到计算峰值，

3.2 计算过程中的权衡

针对特定问题达到某种分类准确度，哪种方法可以提供最有效的解决方案？
1）具有浮点精度的常规ANN？
2）更大的网络，但是BNN？
小型试验
将网络拓扑结构化为3个隐藏层、完全连接的网络，同时缩放每个层中的神经元数量，并绘制Table 1中的结果准确度以及每帧的参数和操作数。

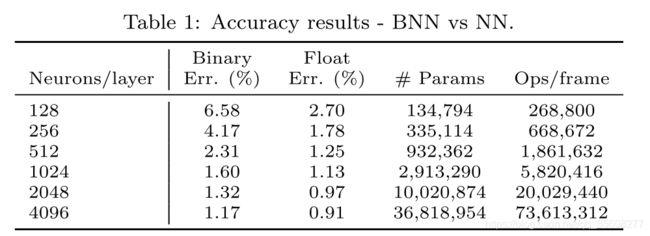
1）随着网络规模的增加，低精度网络和浮点网络之间精度的差异减小;
2）为了达到与浮点网络相同的精度，BNN需要2-11倍以上的参数和操作。

结论
BNN 比CNN好

4 可重构逻辑的BNN

4.1 结构

采用了异构流式架构，如图Figure 2所示。我们为给定的拓扑构建自定义架构，而不是在固定架构之上进行调度操作。独立的计算引擎专用于每个层，通过片上数据流进行通信。一旦前一计算引擎开始产生输出，每个计算引擎就开始计算。此外，由于BNN的紧凑模型尺寸，所有神经网络参数都保存在片上存储器中，这避免了对磁盘存储器的大多数访问，通过重叠计算和通信最小化延迟（完成对一个图像进行分类的时间），最小化启动间隔：上一个图像在计算阵列计算完成后，新图像就可以进入加速器进行计算。将层与计算阵列分开映射也可以实现异构性。

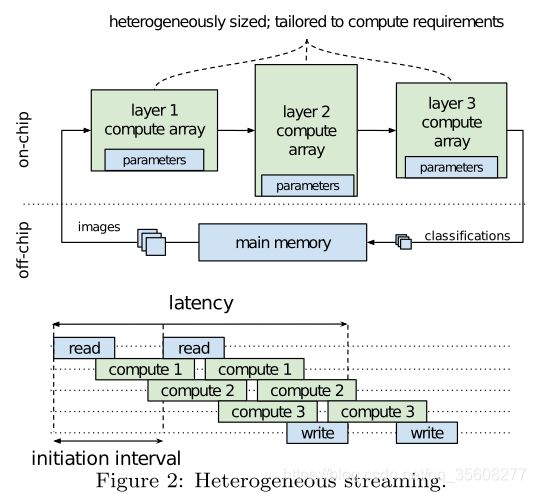
BNN加速器可能需要施加各种约束。 用户强加的约束包括FPGA和平台的选择，所需的分类吞吐量（每秒帧数（FPS）和时钟频率）。 同时，BNN拓扑限制了如何分配计算资源以获得高效的异构流体系结构。

4.2 BNN特定优化

参考第一篇BNN中所描述的方法用于训练本文中的BNN，其中所有BNN层具有以下属性。

*） 对所有输入激活，权重和输出激活（完全二值化）使用1位值，其中未置位表示-1，置位表示+1。

*） 激活功能之前的批量标准化。

*） 使用激活函数 Sign(x) = {+1 if x ≥ 0, −1 if x < 0}

4.2.1 Popcount for Accumulation

BNN计算的规则和值约束性质使得能够以更少的硬件资源计算二进制。硬件的实际结果是二进制点乘积的求和通过popcount操作来实现。该popcount操作是计算设置位的数量而不是使用带符号算术的累加运算。 我们使用Vivado HLS进行的实验表明，与signed-accumulate相比，popcount-accumulate只需要大约一半的LUT和FF资源就能实现。
eg
当时钟Fclk = 200 MHz时，
128位popcount-accumulate需要376个LUT和29个FF，
128位bipolar-accumulate需要759个LUT和84个FF。

4.2.2 Batchnorm-activation as Threshold

可以使用无符号比较计算输出激活，并避免在推理过程中计算批规格化值。
Vivado HLS对16位点积输出值的综合报告表明，正常的batchnorm和符号激活需要2个DSPs、55个FFs和40个LUTs，这里我们描述的阈值激活只需要6个LUTs。

4.2.3 Maxpooling

可以使用或运算有效地实现最大池化max-pooling，并行的对每个元素比较并或合并。

4.3 FINN设计流程和硬件库

4.3.1 Matrix–Vector–Threshold 单元

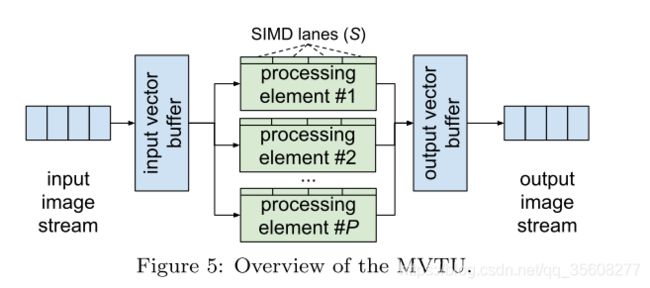
BNN中绝大多数的计算操作都可以表示矩阵-向量运算，然后进行阈值化（Matrix–Vector–Threshold Unit）。MVTU作为一个独立组件实现了完全连接层，并作为卷积层的一部分使用。MVTU的整体组织如图Figure5所示。
eg 激活前的输出aN是全连接神经网络的输出在N的指数，矩阵向量结果aN=A*aN-1b（A是突触权重矩阵，aN-1b是上一层的激活）。激活后的输出可以计算通过abN= aN>τ+N，阈值τ+N确定在4.2.2节描述。

在MVTU内部，由一个输入和输出缓冲区和一个处理元素数组Processing Elements(PEs)组成，每个元素都有一些SIMD通道。可以配置PEs §和SIMD (S)的数量，以控制第4.4.1节中讨论的吞吐量。将要使用的突触权重矩阵保存在PEs之间的片上存储器On-Chip Memory(OCM)中，与输入图像通过MVTU流矩阵相乘。每个PE接收完全相同的控制信号和输入向量数据，但是使用矩阵的不同部分将输入进行多次累加。

图6显示了MVTU PE的数据路径。它把输入向量与突触权重矩阵的一行进行点积计算，并将结果与阈值进行比较，产生一个单比特输出。点积计算是两个位向量之间进行多次累加运算，并用XNOR门实现。接下来，计算结果中的置位的数量，(参见4.2.1节)并将其添加到累加寄存器中。一旦积累了整个点积，它就被限制了。累加器、加法器和阈值内存都是T位宽，可以缩小到T = 1 + log2(Y)以节省额外的资源。

卷积

卷积滤波器的权值被压缩到一个滤波矩阵中，而滑动窗口在输入图像之间移动形成一个图像矩阵。然后将这些矩阵相乘生成输出图像。

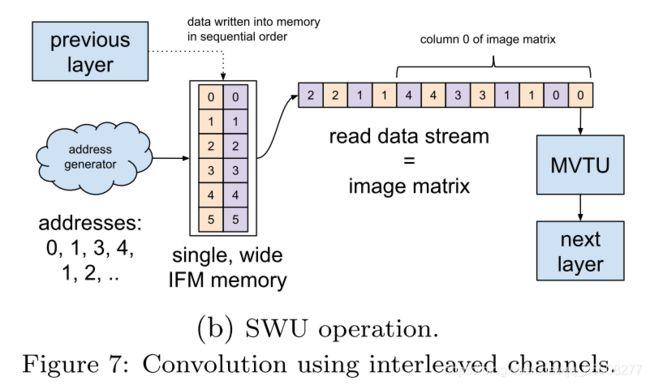
卷积层由滑动窗口单元Sliding Window Unit(SWU)和MVTU组成，SWU从传入的特征图生成图像矩阵，MVTU每次使用与图像矩阵不同的列向量计算矩阵与矩阵的乘积。为了更好地满足MVTU的SIMD并行性和最小化缓冲需求，我们将特征图interleave（交叉）处理，使每个像素包含该位置的所有输入特征图Input Feature Map (IFM)通道数据，如图7a所示

传入的IFM数据简单地存储在缓冲区中的顺序地址上，然后读取每个滑动窗口对应的内存位置，生成图像矩阵。

4.3.3 池化单元Pooling Unit (PU)

实现在C通道DH×DW二进制图像的 k×k 最大池化 ,

PU包含DW位C·k线缓冲区。

4.4 Folding

根据4.3.1节给出的MVTU描述，每个PE对应一个硬件神经元，每个SIMD lane充当一个硬件突触。如果我们在一个网络中对每个MVTU进行维度划分，这个网络中有许多硬件神经元和突触，这些神经元和突触的数量等于BNN层中的神经元和突触的数量，这将产生一个完全并行的神经网络，它可以按照时钟速率对图像进行分类。然而，FPGA上的硬件资源数量是有限的，需要对BNN进行==时间复用(或折叠)==到更少的硬件突触和神经元上。我们现在描述如何在用户约束下执行折叠。
我们考虑了一个更简单的变体，仅控制矩阵-向量乘积的折叠，以实现用户设置给定的FPS需求，并着重于如何根据工作负载映射实现折叠。由于BNN中的几乎所有计算都以矩阵-向量乘法的形式表示，实现折叠形式矩阵-向量乘法已经能够在很大程度上控制系统的吞吐量。折叠也直接影响最终系统的资源和功耗，

4.4.1 矩阵-向量乘积的折叠

通过控制MVTU的两个参数来实现矩阵-向量的折叠:
这些决定了如何在PEs之间划分矩阵。每次处理p高s宽的矩阵，矩阵的每一行映射到不同的PE，每一列映射到不同的SIMD lane。
P为PE的数量，S为每PE的SIMD lanes。

X×Y矩阵,我们称Fn = X / P为neuron fold神经元折叠和Fs = Y / S为synapse fold突触折叠，然后得到total fold F = Fn·Fs，即完成一个矩阵-向量相乘所需的循环次数。注意，Fn和Fs应该是整数，以避免填充权重矩阵。作为一个例子，图Figure 8显示了一个6×4权重矩阵按照三个PEs 两个SIMD lanes进行分割。在这里，每一个矩阵-向量相乘将进行Fn·Fs=(6/3)·(4/2)= 4个循环。
同样的原理也适用于卷积层，但是由于当前的矩阵-矩阵乘积是多个矩阵-向量乘积的实现，所以这些层总是具有一定的折叠量。对于卷积层，total fold为F = Fm·Fn·Fs，其中Fm是由多个矩阵-向量乘积构成的网络依赖常数，等于卷积输出像素的个数。

4.4.2 确定Fn和Fs

分类吞吐量FPS近似为Fclk/IImax
IImax是 the slowest layer的间隔 (with II max )
将所有其他层的吞吐量与瓶颈匹配，使各层的Fn·Fs =Fclk

5. 实验评估

1）SFC和LFC是三层全连接的网络拓扑，用于对MNIST数据集进行分类，使用不同数量的神经元来证明计算的准确性权衡(3.2节)。SFC每层256个神经元，准确率为95.83%，LFC每层1024个神经元，准确率为98.4%。这些网络接受28x28的二进制图像，并输出一个10位one-hot向量来表示该数字。

2）CNV是受BinaryNet[5]和VGG-16[24]启发而设计的卷积网络拓扑。它包含一个连续的(3x3 convolution, 3x3 convolution, 2x2 maxpool)层，重复3次，64-128-256通道，然后是两个完全连接的层，每个层有512个神经元。我们使用这个拓扑对CIFAR-10(80.1%的准确性)和SVHN(94.9%的准确性)数据集进行分类，它们具有不同的权重和阈值。注意，第一层的输入和最后一层的输出不是二值化的；CNV接受24bits/pixel的32x32图像，结果返回一个16bit值的10元素向量。

ref

https://blog.csdn.net/abcdef123456gg/article/details/84452681