【路径规划】基于matlab蚁群的多无人机攻击调度【含Matlab源码 034期】
一、简介
蚁群算法是模拟蚁群觅食行为的一种优化算法。在整个觅食过程中蚂蚁散播信息素,蚂蚁通过感知到的信息素多少,来决定所要选择的下一个栅格。
在初始阶段,由于地面上没有信息素,因此蚁群的行走路径是随机的,蚂蚁在行走的过程中会不断释放信息素,标识自己行走的路径。随着时间的推移,有若干只蚂蚁找到了食物,此时便存在若干条从洞穴到食物的路径。由于蚂蚁的行为轨迹是随机分布的,因此在单位时间内,短路径上的蚂蚁数量比长路径上的蚂蚁密度要大,短路径留下的信息素浓度也越高。这为后面的蚂蚁们提供了有力的方向指引,越来越多的蚂蚁聚集到最短的路径上去。对于单个蚂蚁来说,它并没有要寻找最短路径,只是根据概率选择;对于整个蚁群系统来说,它们却达到了寻找到最优路径的客观上的效果。
假设蚁群中蚂蚁的总数为M,各蚂蚁在栅格环境下移动,并且根据状态转移规则选择下一个栅格,假设在时刻t时,蚂蚁k位于栅格i,那么蚂蚁k选择下一个栅格j的概率为:
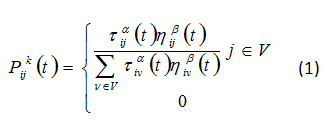
(1)式中:V表示蚂蚁K可以选择下一个栅格的集合;Alpha为信息素浓度启发因子,Alpha越大,表明蚂蚁K越趋向于选择多数蚂蚁走过的路径;Beta表示期望启发因子,反映了能见度信息对蚂蚁选择下一步位置所起作用的大小,Beta值越大,表明蚂蚁K越趋向于选择距离目标点近的栅格,越倾向于往能见度程。表示t时刻路径(i,j)上的信息素浓度;表示t时刻路径(i,j)上的启发信息,其定义为:


蚁群算法的核心部分在于模拟了蚁群的转移概率选择行为,通过使用信息素和启发式函数值进行转移概率计算。其中蚂蚁状态转移过程中以节点到目标点之间的距离的倒数作为启发信息,不利于障碍物的预先规避。并且在复杂的路径规划环境下,蚁群算法在一个庞大的空间中搜索,在优化初期路径上的信息素浓度较小,正向反馈信息不明显尤其是随机解产生的过程中的“盲目搜索”产生大量的局部交叉路径,降低蚁群算法的运行效率,且容易陷入局部最优,搜索进行到一定程度后,容易出现停滞现象,所有个体发现的解完全一致,不能进行进一步搜索,不利于发现更好的解。
二、源代码
t=[4 5;16 25.8;10 45;20 55;30 65;35 55;29 31;37 26;47 27;30 31.3;31 17;14 7;35.6 13.8;26.7 22.5;21 39;38 42;5 26;28 53;20 13;10 60;26 31;54 38;7 58;12 36;30 2] %24个点,第25个点事origin
save t.mat t
load t.mat
value=[1 1 1 2 3 2 1 3 3 2 2 2 2 2 1 2 3 3 1 1 2 1 1 1]; %24个目标的价值
value=value/100;
time=zeros(1,25); %侦察UAV时间数组,里面放的是飞机走的航程,除以速度便是时间,设速度为‘1’
attacktime=zeros(1,25); %打击UAV时间数组
%把侦察过的任务对应无人机走过的航程存到该任务的一个矩阵里,当做时间,然后打击任务如果选定某任务,check一下时间是否合格,合格的话,可以打击,并存入禁忌表,不合格的话,选次概率的
%注:目的是把所有目标执行完所有任务,所以每次迭代最后所有无人机收获的总价值都一样,都是所有目标的价值之和;所以本程序考虑优先执行价值大的目标,防止无人机飞很久、打很久后攻打效率变低
%的情况出现
%%计算城市间相互距离
n=size(t,1);
D=zeros(n,n);
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((t(i,:)-t(j,:)).^2));
else
D(i,j)=1e-2;
end
end
end
%%初始化参数
m=10; %蚂蚁个数
alpha=1; %信息素重要程度因子
beta=1; %启发函数重要程度因子
gama=2;
rho=0.3; %信息素挥发因子
Q=1.0; %总量
eta=1./D; %启发函数
tau=ones(n,n)+7.1192e-005;%信息素矩阵
iter=1; %迭代次数初始值
iter_max=80; %迭代次数最大值
length_best=zeros(iter_max,1);%每次迭代最佳路径长度(应该是一次比一次小)
length_ave=zeros(iter_max,1); %每次迭代路径平均长度
%%迭代寻找最佳路径
while iter<=iter_max
whta=cell(8,1);
lieend=zeros(8,1);
for zu=1:8
city_index=1:25; %城市来标号
table=[];
start=zeros(4,1);
temp=randperm(24);
for i=1:4
start(i)=temp(i);
end
table(:,1)=start;
j=2;
while (j<=30)
for i=1:4
if i==1 %UAV1只负责“侦察”任务
if table(1,(j-1))~=25
table1=table(1,:);
table1=[table1;table(3:4,:)];
tabu1=table1(:); %UAV1的禁忌表出来了 %25如果也在tabu1里的话,那么
allow_index1=~ismember(city_index,tabu1); %【走过的变成0,能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1...)】【注意:allow_index与city_index同维】
allow1=city_index(allow_index1); %把还能走的序号摘出来了(待访问的城市集合)
P1=allow1;
%计算城市的转移概率
if numel(allow1)~=0
for k=1:max(size(allow1))-1
P1(k)=(tau(table(1,(j-1)),allow1(k))^alpha)*(eta(table(1,(j-1)),allow1(k))^beta)*10000+7.1192e-004;
end
P1(max(size(allow1)))=7.1192e-005;
P1=P1/sum(P1);
[d1,ind1]=sort(P1,2,'descend');%从大到小排序是d1,对应的原序号是ind1
target1=allow1(ind1(1));
%轮盘赌法选择下一个城市
%pc1=cumsum(P1); % (p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 ....)【p1<->allow(1) p2<->allow(2) ...】
%target_index1=find(pc1>=rand);
%target1=allow1(target_index1(1)); %这次返回的是allow数组中城市的真正序号
table(1,j)=target1; %把选好这个点放到路径表里面
rr=D(25,table(1,1));
time(table(1,1))=rr;
if j>2
for c=2:(j-1)
rr=rr+D(table(1,c-1),table(1,c));
end
end
rrr=rr+D(table(1,j-1),target1);%rrr就是UAV1到该点时走过的航程
time(target1)=rrr;
else
table(1,j)=25;
end
end
if table(1,(j-1))==25
table(1,j)=25;
end
end
if i==2 %UAV2只负责“打击”任务
if (table(2,(j-1))~=25)
table(2,1)=table(1,1); %设定它第一次打击的是UAV1侦察过的目标
ta2=table(1:(4*(j-1)+1)); %当前元素之前所有的元素
tabu21=[];
tabu22=[];
tabu2=[];
for y=1:24
if sum(ta2==y)==2
tabu21=[tabu21;y];
end
end %出现过两次的放在tabu21里
tabu22=setdiff(1:24,ta2); %一次都没出现的放在tabu22里
tabu2=[tabu21',tabu22]; %tabu2出来了
allow_index2=~ismember(city_index,tabu2); %【走过的变成0,能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1...)】【注意:allow_index与city_index同维】
allow2=city_index(allow_index2); %把还能走的序号摘出来了(待访问的城市集合)
P2=allow2;
%计算城市的转移概率
for k=1:(length(allow2)-1)
P2(k)=tau(table(2,(j-1)),allow2(k))*eta(table(2,(j-1)),allow2(k))*value(allow2(k))*10000;
end
P2(max(size(allow2)))=7.1192e-005;
P2=P2/sum(P2);
[d2,ind2]=sort(P2,2,'descend');%从大到小排序是d1,对应的原序号是ind1
target2=allow2(ind2(1)); %target2=d1(1);
%轮盘赌法选择下一个城市
%pc2=cumsum(P2); % (p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 ....)【p1<->allow(1) p2<->allow(2) ...】
%target_index2=find(pc2>=rand); %选中那个概率较大的选中的点,返回的是allow数组中的序号
%target2=allow2(target_index2(1)); %这次返回的是allow数组中城市的真正序号
%table(2,j)=target2; %把选好这个点放到路径表里面
oo=D(25,table(2,1));
attacktime(table(2,1))=oo;
if j>2
for c=2:(j-1)
oo=oo+D(table(2,c-1),table(2,c));
end
end
ooo=oo+D(table(2,j-1),target2);%ooo就是UAV2到该点时走过的航程
if numel(d2)>5
u=2;
while (ooo>time(target2)+20 & u<6)
target2=allow2(ind2(u));
ooo=oo+D(table(2,(j-1)),target2);
u=u+1;
end
end
table(2,j)=target2;
attacktime(target2)=ooo;
end
if table(2,(j-1))==25
table(2,j)=25;
end
end
if i==3 %UAV3是“察打”任务
if table(3,(j-1))~=25
ta3=table(1:(4*(j-1)+2));
tabu3=[];
tabu3c=[];
for y=1:24
if sum(ta3==y)==2
tabu3=[tabu3;y];
end
end %出现两次的放在tabu3里
for y=1:24
if sum(ta3==y)==1
tabu3c=[tabu3c;y];
end
end %tabu3c是待打的任务,已侦查完的任务
allow_index3=~ismember(city_index,tabu3); %【走过的变成0,能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1...)】【注意:allow_index与city_index同维】
allow3=city_index(allow_index3); %把还能走的序号摘出来了(待访问的城市集合)
P3=allow3;
%计算城市的转移概率
for k=1:(length(allow3)-1)
%if ismember(allow3(k),tabu3c)==1
h=table(3,(j-1))
P3(k)=(tau(table(3,j-1),allow3(k))^alpha)*(eta(table(3,(j-1)),allow3(k))^beta)*value(allow3(k))*10000+7.1192e-005;%这是要打的,需要价值
%else
%P3(k)=(tau(table(3,(j-1)),allow3(k))^alpha)*(eta(table(3,(j-1)),allow3(k))^beta)*100+7.1192e-005;%这些是待侦察的,没有价值
%end
end
P3(max(size(allow3)))=7.1192e-009;
P3=P3/sum(P3);
[d3,ind3]=sort(P3,2,'descend');%从大到小排序是d1,对应的原序号是ind1
target3=allow3(ind3(1));
%轮盘赌法选择下一个城市
%pc3=cumsum(P3); % (p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 ....)【p1<->allow(1) p2<->allow(2) ...】
%target_index3=find(pc3>=rand); %选中那个概率较大的选中的点,返回的是allow数组中的序号
%target3=allow3(target_index3(1)); %这次返回的是allow数组中城市的真正序号
%table(3,j)=target3; %把选好这个点放到路径表里面
ww=D(25,table(3,1));
time(table(3,1))=ww;
if j>2
for c=2:(j-1)
ww=ww+D(table(3,c-1),table(3,c));
end
end
www=ww+D(table(3,j-1),target3);%www就是UAV3到该点时走过的航程
if ismember(target3,tabu3c)==0 %侦察任务
time(target3)=www;
table(3,j)=target3;
else %打击任务
attacktime(target3)=www;
if numel(d3)>5
u=2;
while (www>time(target3)+20 & u<6)
target3=allow3(ind3(u));
www=ww+D(table(3,(j-1)),target3);
u=u+1;
end
end
attacktime(target3)=www;
table(3,j)=target3;%www<time(target3)+10 说明此打击任务合理
end
end
if table(3,(j-1))==25
table(3,j)=25;
end
end
if i==4 %UAV4是“察打”任务
if table(4,(j-1))~=25
ta4=table(1:(4*(j-1)+3));
tabu4=[];
tabu4c=[];
for y=1:24
if sum(ta4==y)==2
tabu4=[tabu4;y];
end
end %出现两次的放在tabu4里、、可以把已经侦察过的放在tabu4c中,(即出现过一次的),如果选到的是在tabu4'中的说明是要打击的然后算一下它的航程,再和侦察路径比较
for y=1:24
if sum(ta4==y)==1
tabu4c=[tabu4c;y];
end
end
allow_index4=~ismember(city_index,tabu4); %【走过的变成0,能走的为1】【若tabu=(1 4)则allow_index=(0 1 1 0 1 1 1...)】【注意:allow_index与city_index同维】
allow4=city_index(allow_index4); %把还能走的序号摘出来了(待访问的城市集合)
P4=allow4;
%计算城市的转移概率
for k=1:(max(size(allow4))-1)
%if ismember(allow4(k),tabu4c)==1
sxx=table(4,(j-1))
P4(k)=(tau(table(4,(j-1)),allow4(k))^alpha)*(eta(table(4,(j-1)),allow4(k))^beta)*value(allow4(k))*10000+7.1192e-005;
%else
%P4(k)=(tau(table(4,(j-1)),allow4(k))^alpha)*(eta(table(4,(j-1)),allow4(k))^beta)*100+7.1192e-005;
%end
end
P4(max(size(allow4)))=7.1192e-009;
P4=P4/sum(P4);
[d4,ind4]=sort(P4,2,'descend');%从大到小排序是d1,对应的原序号是ind1
target4=allow4(ind4(1));
%轮盘赌法选择下一个城市
%pc4=cumsum(P4); % (p1 p1+p2 p1+p2+p3 p1+p2+p3+p4 ....)【p1<->allow(1) p2<->allow(2) ...】
%target_index4=find(pc4>=rand); %选中那个概率较大的选中的点,返回的是allow数组中的序号
%target4=allow4(target_index4(1)); %这次返回的是allow数组中城市的真正序号
%table(4,j)=target4; %把选好这个点放到路径表里面
qq=D(25,table(4,1));
time(table(4,1))=qq;
if j>2
for c=2:(j-1)
qq=qq+D(table(4,c-1),table(4,c));
end
end
qqq=qq+D(table(4,j-1),target4);%www就是UAV3到该点时走过的航程
if ismember(target4,tabu4c)==0 %侦察任务
time(target4)=qqq;
table(4,j)=target4;
else %打击任务
attacktime(target4)=qqq;
if numel(d4)>5
u=2;
while (qqq>time(target4)+20 & u<6)
target4=allow4(ind4(u));
qqq=qq+D(table(4,j-1),target4);
u=u+1;
end
end
attacktime(target4)=qqq;
table(4,j)=target4;%www<time(target4)+10 说明此打击任务合理
end
end
if table(4,(j-1))==25
table(4,j)=25;
end
end
end %一列结束
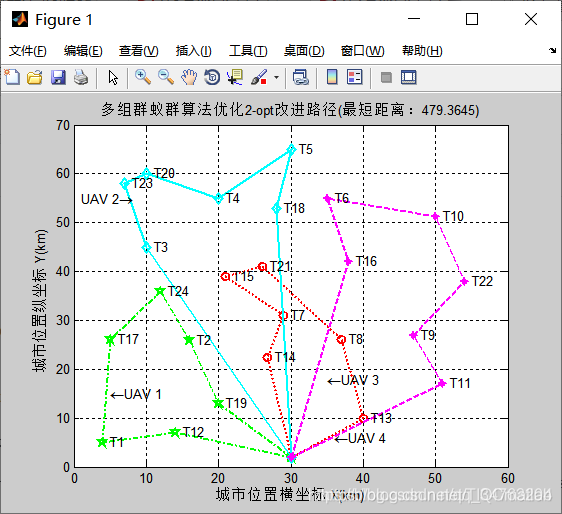
三、运行结果
四、备注
完整代码或者代写添加QQ2449341593
往期回顾>>>>>>
【VRP】基于matlab遗传算法的带时间窗的车辆路径问题【含Matlab源码 002期】
【路径规划】基于matlab A*算法解决三维路径规划问题【含Matlab源码 003期】
【路径规划】基于matlab人工蜂群的路径规划【含Matlab源码 004期】
【路径规划】基于matlab蚁群求解多旅行商MTSP问题【含Matlab源码 005期】
【路径规划】基于matlab蚁群算法的无人机路径规划【含Matlab源码 008期】
【路径规划】基于matlab遗传算法求解多VRP问题【含Matlab源码 010期】
【路径规划】基于matlab遗传算法的多中心VRP求解【含Matlab源码 011期】
【路径规划】基于matlab粒子群的三维无人机路径规划【含Matlab源码 015期】
【路径规划】基于matlab采用遗传算法编制多物流中心的开放式车辆路径问题【含Matlab源码 017期】
【路径规划】基于matlab粒子群之机器人栅格路径规划【含Matlab源码 018期】
【路径规划】基于matlab蚁群算法求解最短路径【含Matlab源码 019期】
【路径规划】基于matlab 免疫算法之物流中心选址问题【含Matlab源码 020期】
【路径规划】基于matlab人工蜂群的无人机三维路径规划【含Matlab源码 021期】
【路径规划】基于matalb栅格地图——遗传算法的机器人最优路径规划【含Matlab源码 022期】
【路径规划】基于matlab栅格地图——遗传算法的机器人最优路径规划【含Matlab源码 027期】