cpp简单实现一下RNN神经网络
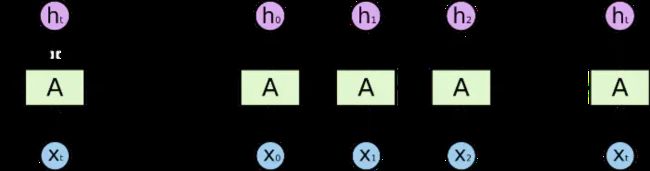
RNN的结构
t a n h ( x ) = e x − e − x e x + e − x tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} tanh(x)=ex+e−xex−e−x
S o f t m a x ( X ) = e X ∑ i e x i Softmax(X)=\frac{e^X}{\sum_i{e^{x_i}}} Softmax(X)=∑iexieX
t a n h ( x ) tanh(x) tanh(x)是非线性函数,使用非线性函数增强神经网络表达力,(。・∀・)ノ゙
S o f t m a x ( x ) Softmax(x) Softmax(x)来处理最后的处理结果,计算每种结果的概率,在反向传播时的效果比最小二乘法更好┗|`O′|┛
前向传播
X i = t a n h ( U i X i − 1 + V i H i + B i ) X_i=tanh\left( U_i X_{i-1} + V_i H_i + B_i \right) Xi=tanh(UiXi−1+ViHi+Bi)
H i = X i H_i=X_i Hi=Xi
- X i X_i Xi 是第i层的输出向量
- H i H_i Hi 是第i层的上个时刻输出向量
- U i , V i U_i,V_i Ui,Vi分别是对输入数据处理的权重矩阵
- B i B_i Bi是偏置
- 每层神经网络按照这个公式递推就可以了
- 用Softmax对最后一层处理
反向传播
对于每次的计算,求取其梯度,然后用梯度更新参数
∂ ε ( t ) ∂ U i = ∂ ε ( t ) ∂ X n ( t ) ∏ k = i + 1 n ∂ X k ( t ) ∂ X k − 1 ( t ) ( ∑ k = 1 t + 1 ( ∂ X k − 1 ∂ U i ∏ T = k t ∂ X i ( T ) ∂ X i ( T − 1 ) ) ) \frac{\partial \varepsilon\left(t\right)}{\partial U_i}=\frac{\partial \varepsilon\left(t\right)}{\partial X_n\left(t\right)} \prod_{k=i+1}^{n}\frac{\partial X_{k}\left(t\right)}{\partial X_{k-1}\left(t\right)} \left( \sum_{k=1}^{t+1} \left( \frac{\partial X_{k-1}}{\partial U_i} \prod_{T=k}^{t}\frac{\partial X_i\left(T\right)}{\partial X_i\left(T-1\right)}\right) \right) ∂Ui∂ε(t)=∂Xn(t)∂ε(t)k=i+1∏n∂Xk−1(t)∂Xk(t)(k=1∑t+1(∂Ui∂Xk−1T=k∏t∂Xi(T−1)∂Xi(T)))
∂ ε ( t ) ∂ U i = ∂ ε ( t ) ∂ X n ( t ) ∏ k = i + 1 n ∂ X k ( t ) ∂ X k − 1 ( t ) ( ∑ k = 1 t + 1 ( ∂ X k − 1 ∂ V i ∏ T = k t ∂ X i ( T ) ∂ X i ( T − 1 ) ) ) \frac{\partial \varepsilon\left(t\right)}{\partial U_i}=\frac{\partial \varepsilon\left(t\right)}{\partial X_n\left(t\right)} \prod_{k=i+1}^{n}\frac{\partial X_{k}\left(t\right)}{\partial X_{k-1}\left(t\right)} \left( \sum_{k=1}^{t+1} \left( \frac{\partial X_{k-1}}{\partial V_i} \prod_{T=k}^{t}\frac{\partial X_i\left(T\right)}{\partial X_i\left(T-1\right)} \right) \right) ∂Ui∂ε(t)=∂Xn(t)∂ε(t)k=i+1∏n∂Xk−1(t)∂Xk(t)(k=1∑t+1(∂Vi∂Xk−1T=k∏t∂Xi(T−1)∂Xi(T)))
∂ ε ( t ) ∂ U i = ∂ ε ( t ) ∂ X n ( t ) ∏ k = i + 1 n ∂ X k ( t ) ∂ X k − 1 ( t ) ( ∑ k = 1 t + 1 ( ∂ X k − 1 ∂ B i ∏ T = k t ∂ X i ( T ) ∂ X i ( T − 1 ) ) ) \frac{\partial \varepsilon\left(t\right)}{\partial U_i}=\frac{\partial \varepsilon\left(t\right)}{\partial X_n\left(t\right)} \prod_{k=i+1}^{n}\frac{\partial X_{k}\left(t\right)}{\partial X_{k-1}\left(t\right)} \left( \sum_{k=1}^{t+1} \left( \frac{\partial X_{k-1}}{\partial B_i} \prod_{T=k}^{t}\frac{\partial X_i\left(T\right)}{\partial X_i\left(T-1\right)} \right) \right) ∂Ui∂ε(t)=∂Xn(t)∂ε(t)k=i+1∏n∂Xk−1(t)∂Xk(t)(k=1∑t+1(∂Bi∂Xk−1T=k∏t∂Xi(T−1)∂Xi(T)))
求其梯度的式子很长,需要追溯到上层神经网络的输出和其他时刻的时候神经网络的输出,所也要用递推的方法求梯度
代码实现
#include用 a b c d e 训练RNN