《神经网络与深度学习》-注意力机制与外部记忆
注意力机制与外部记忆
-
- 1. 认知神经学中的注意力
- 2. 注意力机制
-
- 2.1 注意力机制的变体
-
- 2.1.1 硬性注意力
- 2.1.2 键值对注意力
- 2.1.3 多头注意力
- 2.1.4 结构化注意力
- 2.1.5 指针网络
- 3. 自注意力模型
- 4. 人脑中的记忆
- 5. 记忆增强神经网络
-
- 5.1 端到端记忆网络
- 5.2 神经图灵机
- 6. 基于神经动力学的联想记忆
-
- 6.1 Hopfield网络
- 6.2 使用联想记忆增加网络容量
前馈网络和循环网络拟合能力很强,但由于优化算法和计算能力的限制,实践中难以达到通用近似的能力。处理复杂任务时,计算机的计算能力仍是限制神经网络发展的瓶颈。
为减少计算复杂度,借鉴生物神经网络的机制,引入了局部连接、权重共享、汇聚操作简化神经网络结构,缓解模型复杂度和表达能力之间的矛盾,但仍希望通过不过度增加模型复杂度来提高模型表达能力。
神经网络中可以存储的信息量称为网络容量。一组神经元的存储容量和神经元的数量和网络的复杂度成正比。
人脑同样存在网络容量问题,人脑记忆只有几秒,但人脑有注意力机制和记忆机制两个问重要机制来解决信息过载的问题。
借鉴人脑的机制,提高神经网络处理信息的能力,注意力:通过自上而下的信息选择机制来过滤大量无关信息;引入外部记忆:优化神经网络的记忆结构来提高神经网络存储信息的容量。
1. 认知神经学中的注意力
注意力是指,人可以关注一些信息的同时忽略另一些信息的选择能力。人脑接受大量感觉输入,但人脑可以有意或无意地从大量输入信息中选择小部分有用信息来重点处理,并忽略其他信息,这种能力注意力(Attention),注意力可用在外部刺激(听觉、视觉、味觉),也可以作用在内部意识(思考、回忆)。注意力常分为两类:
- 自上而下的有意识的注意力,聚焦式注意力(Focus Attention):有预订目的、依赖任务的,主动有意识地聚焦于某一对象的注意力
- 自下而上的无意识的注意力,基于显著性的注意力(Saliency-Based Attention):由外界刺激驱动的注意,不需要主动干预,和任务无关。如果一个对象的刺激信息不同于其周围信息,一种无意识的的赢者通吃(Winner-Take-All)或者门控(Gating)机制就可以把注意力转向这个对象。记忆信息、阅读、思考等大部分人脑活动依赖于有意识、无意识的注意力。
鸡尾酒会效应:一个人在吵闹的鸡尾酒会上和朋友聊天,周围噪声多,仍可以听到朋友的谈话,而忽略其他人的声音(聚焦式注意力),如果未注意到背景中有重要的词(如他的名字),他会马上注意到(显著性注意力)。
聚焦式注意力会随着环境、情景或任务不同而选择不同的信息。找人时,专注于每个人的脸部,统计人数时,专注于每个人的轮廓。
2. 注意力机制
计算能力有限的情况下,注意力机制(Attention Mechanism)作为一种资源分配方案,将有限计算资源用来处理更重要的信息,是解决信息过载的主要手段。
目前的网络中,最大汇聚(池化)、门控机制可近似地看做自下而上的基于显著性的注意力机制。自上而下的聚焦式注意力,也是有效的信息选择方式,以阅读理解为例,对长文章的内容提问,问题之和段落中的一两个句子相关,其余无关,为减小神经网络的计算负担,只需把相关的片段挑选出来,让后续的神经网络处理,而不是输入所有的文章给网络。
用 X = [ x 1 , ⋯ , x N ] ∈ R D × N \pmb{X} = [\pmb{x_1}, \cdots, \pmb{x_N}] \in \R^{D \times N} XXX=[x1x1x1,⋯,xNxNxN]∈RD×N 表示 N 组输入信息,其中 D 维向量 x n ∈ R D \pmb{x}_n \in \R^D xxxn∈RD, n ∈ [ 1 , N ] n \in [1, N] n∈[1,N] 表示一组输入信息。注意力机制从 X \pmb{X} XXX中挑选一些和任务相关的信息输入到网络,计算步骤:
- 在所有输入信息上计算注意力分布
- 根据注意力分布计算输入信息的加权平均
注意力分布 为了从 N 个输入向量 [ x 1 , ⋯ , x N ] [\pmb{x}_1, \cdots,\pmb{x}_N] [xxx1,⋯,xxxN] 中选出和某个特定任务相关的信息,引入一个和任务相关的表示,称为查询向量(Query Vector) ,并通过一个打分函数来计算每个输入向量和查询向量之间的相关性。
给定一个和任务相关的查询向量 q \pmb{q} qqq,我们用注意力机制 z ∈ [ 1 , N ] z \in [1,N] z∈[1,N] 来表示被选择信息的索引位置,即 z = n 表示选择了第 n 个输入向量,为了便于计算,采用软性信息选择机制。首先计算在给定 q \pmb{q} qqq 和 X \pmb{X} XXX下,选择第 i 个输入向量的概率 α n \alpha_n αn:

其中 α n \alpha_n αn 称为注意力分布(Attention Distribution), s ( x , q ) s(\pmb{x}, \pmb{q}) s(xxx,qqq) 为注意力打分函数,可以使用以下几种方式计算:
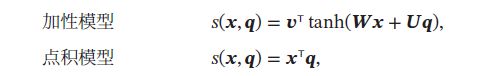
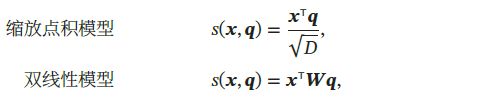
其中 W , U , v \pmb{W}, \pmb{U}, \pmb{v} WWW,UUU,vvv 为可学习的参数,D为输入向量的维度。理论上,\pmb{W}, 加性模型和点积模型的复杂度差不多,但点积模型在实现上可以更好地利用矩阵乘积,计算效率更高。当输入向量的维度D比较高时,点积模型的值通常具有较大的方差,从而导致softmax函数的梯度比较小。故缩放点积模型可以很好地解决这个问题。双线性模型课看做是一种泛化的点积模型,假设 W = U T V \pmb{W} = \pmb{U}^T\pmb{V} WWW=UUUTVVV ,双线性模型可写成 s ( x , q ) = x T U T V q = ( U x ) T V q s(\pmb{x} ,\pmb{q}) = \pmb{x}^T\pmb{U}^T\pmb{V}\pmb{q}= (\pmb{Ux})^T\pmb{Vq} s(xxx,qqq)=xxxTUUUTVVVqqq=(UxUxUx)TVqVqVq,即分别对 x \pmb{x} xxx和 q \pmb{q} qqq进行线性变换后计算点积。相比点积模型,双线性模型在计算相似度时引入了非对称性。
加权平均 注意力分布 α n \alpha_n αn可以用来解释在给定任务相关的查询 q \pmb{q} qqq 时,第 n 个输入向量受关注的程度,采用一种软性的信息选择机制对输入信息进行汇总,即:

上式称为软性注意力机制(Soft Attention Mechanism)。注意力机制可以单独使用,但更多作为神经网络汇总的一个组件,示例:
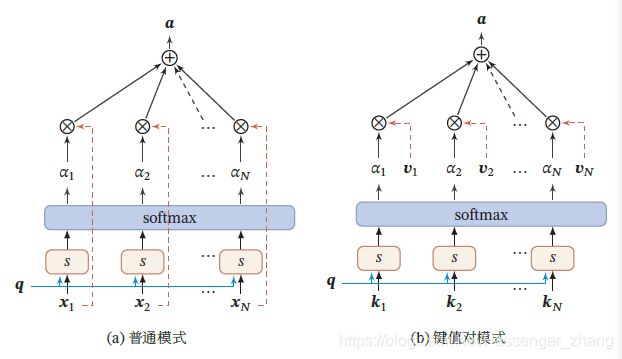
2.1 注意力机制的变体
2.1.1 硬性注意力
软性注意力所选择的信息是所有输入向量在注意力分布下的期望,而硬性注意力(Hard Attention)只关注某一个输入向量。两种实现方式:
- 选取最高概率的一个输入向量,即
a t t ( X , q ) = x n ^ att(\pmb{X},\pmb{q}) = \pmb{x}_{\hat{n}} att(XXX,qqq)=xxxn^
其中 n ^ \hat{n} n^为概率最大的输入向量的下标,即 n ^ = arg n = 1 N m a x α n \hat{n} = \arg_{n=1}^{N}max \alpha_n n^=argn=1Nmaxαn。
- 通过在注意力分布式上随机采样的方式实现。
硬性注意力缺点:基于最大采样或随机采样的方式选择信息,会使得最终的损失函数与注意力分布之间的函数关系不可导,因此无法使用反向传播算法训练。为使用反向传播算法,常采用软性注意力代替硬性注意力。
2.1.2 键值对注意力
用键值对格式来表示输入信息,其中“键”用来计算注意力分布 α n \alpha_n αn,“值”用来计算聚合信息。
用 ( K , V ) = [ ( k 1 , v 1 ) , ⋯ , ( k N , v N ) ] (K,V)=[(\pmb{k}_1,\pmb{v}_1),\cdots,(\pmb{k}_N,\pmb{v}_N)] (K,V)=[(kkk1,vvv1),⋯,(kkkN,vvvN)] 表示N组输入信息,给定任务相关的查询向量 q \pmb{q} qqq 时,注意力函数如下, s ( k n , q ) s(\pmb{k}_n, \pmb{q}) s(kkkn,qqq)为打分函数:

键值对注意力机制实例,当 K = V K=V K=V时,键值对模式等价于普通的注意力机制:

2.1.3 多头注意力
多头注意力(Multi-Head Attention)是利用多个查询 Q = [ q 1 , ⋯ , q M ] Q = [\pmb{q}_1, \cdots, \pmb{q}_M] Q=[qqq1,⋯,qqqM],来并行地从输入信息中获取多组信息,每个注意力关注输入信息的不同部分。
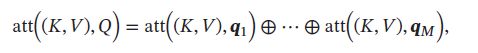
其中 ⨁ \bigoplus ⨁ 表示向量拼接。
2.1.4 结构化注意力
之前的介绍,假设所有的输入信息是同等重要的,是扁平(Flat)结构,注意力分布实际上是在所有输入信息上的多项式分布。
但如果输入信息是层次(hierarchical)结构,比如文本可以分为词、句子、段落、篇章等不同粒度层次,可用层次化的注意力来进行更好的信息选择。
此外,假设注意力分为上下文相关的二项分布,可用图模型构建更复杂的结构化注意力分布。
2.1.5 指针网络
注意力机制主要是用来做信息筛选,从输入信息中选取相关的信息。注意力机制可分为两步:1.计算注意力分布 α \alpha α,2.根据 α \alpha α来计算输入信息的加权平均。可以只利用注意力机制中的第一步,将注意力分布作为一个软性的指针来指出相关信息的位置。
指针网络是一种序列到序列模型,输入为长度为N的向量 : X = x 1 , ⋯ , x N \pmb{X}=\pmb{x}_1,\cdots,\pmb{x}_N XXX=xxx1,⋯,xxxN。输出是长度为M的下标序列: c 1 : M = c 1 , c 2 , ⋯ , c M , c M ∈ [ 1 , N ] , ∀ m \pmb{c}_{1:M}=c_1, c_2, \cdots,c_M, c_M \in [1,N], \forall m ccc1:M=c1,c2,⋯,cM,cM∈[1,N],∀m。比如输入是一组乱序的数字,输出是按大小排序的输入数字序列的下标。
条件概率 p ( c 1 : M ∣ x 1 : N ) p(c_{1:M}|\pmb{x}_{1:N}) p(c1:M∣xxx1:N)可以写成:

其中条件概率 p ( c m ∣ x c 1 , ⋯ , x c ( m − 1 ) , x 1 : N ) p(c_m|\pmb{x}_{c_1},\cdots,\pmb{x}_{c_{(m-1)}},\pmb{x}_{1:N}) p(cm∣xxxc1,⋯,xxxc(m−1),xxx1:N) 课通过注意力分布来计算。假设用一个RNN对 x c 1 , ⋯ , x c ( m − 1 ) , x 1 : N \pmb{x}_{c_1},\cdots,\pmb{x}_{c_{(m-1)}},\pmb{x}_{1:N} xxxc1,⋯,xxxc(m−1),xxx1:N 进行编码得到向量 h m \pmb{h}_m hhhm ,则:
![]()
其中 s m , n s_{m,n} sm,n 为在解码过程中第 m 步时, h m \pmb{h}_m hhhm对 h n \pmb{h}_n hhhn 的未归一化的注意力分布,即:
![]()
其中 v , W , U \pmb{v}, \pmb{W}, \pmb{U} vvv,WWW,UUU为可学习的参数。
下图是指针网络的示例,其中 h 1 , h 2 , h 3 \pmb{h}_1,\pmb{h}_2,\pmb{h}_3 hhh1,hhh2,hhh3为输入数字20,5,10经过RNN的隐状态, h 0 \pmb{h}_0 hhh0 对应一个字符 < < <,当输入 > > > 时,网络一步一步输出三个输入数字从大到小排序的下标。
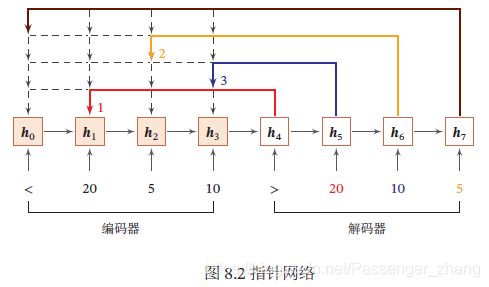
3. 自注意力模型
使用神经网络处理变长向量序列时,通常可以使用CNN或RNN进行编码来得到一个相同长度的输出向量序列:
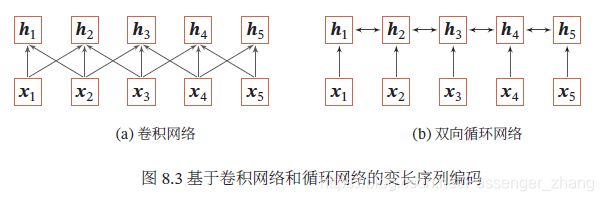
基于CNN或RNN的序列编码可看做一种局部编码方式,只建模了输入信息的局部依赖关系,虽然RNN理论上可建立长距离依赖关系,但由于信息传递的容量以及梯度消失问题,只能建立短距离依赖关系。
建立输入序列之间的长距离依赖关系的两种方法:1.增加网络层数,通过一个深层网络获取远距离信息交互;2.使用全连接网络。全连接网络是非常直接的建模远距离依赖的模型,但无法处理变长的输入序列。不同输入长度,连接权重的大小也不同。可用注意力机制来动态生成不同连接的权重,即自注意力模型(Self-Attention Model)。
自注意力模型采用查询-键-值(Query-Key-Value,QKV)。计算过程如下,红色字母表示矩阵维度:
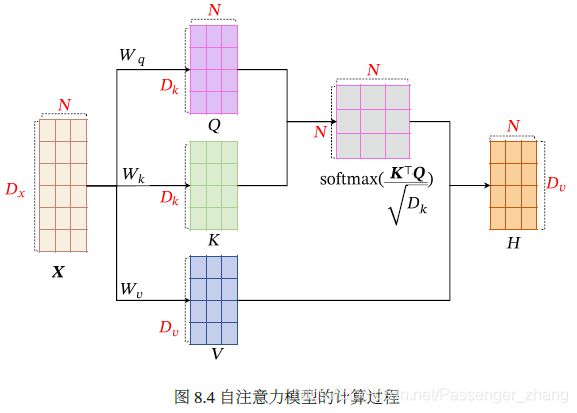
假设输入序列为 X = [ x 1 , ⋯ , x N ] ∈ R D x × N \pmb{X}=[\pmb{x}_1,\cdots,\pmb{x}_N] \in \R^{D_x \times N} XXX=[xxx1,⋯,xxxN]∈RDx×N,输出序列为 H = [ h 1 , ⋯ , h N ] ∈ R D v × N \pmb{H}=[\pmb{h}_1,\cdots,\pmb{h}_N] \in \R^{D_v \times N} HHH=[hhh1,⋯,hhhN]∈RDv×N.自注意力模型计算过程如下:
- 对于每个输入 x i \pmb{x}_i xxxi ,首先将其线性映射到三个不同的空间,得到查询向量 q i ∈ R D k \pmb{q}_i \in \R^{D_k} qqqi∈RDk、查询向量 k i ∈ R D k \pmb{k}_i \in \R^{D_k} kkki∈RDk、
查询向量 v i ∈ R D v \pmb{v}_i \in \R^{D_v} vvvi∈RDv。
对于整个输入序列 X \pmb{X} XXX,线性映射过程可以简写为:
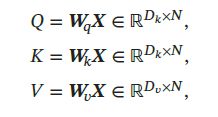
其中 W q ∈ R D k × D x \pmb{W}_q \in \R^{D_k \times D_x} WWWq∈RDk×Dx、 W k ∈ R D k × D x \pmb{W}_k \in \R^{D_k \times D_x} WWWk∈RDk×Dx、 W v ∈ R D v × D x \pmb{W}_v \in \R^{D_v \times D_x} WWWv∈RDv×Dx分别为线性映射的参数矩阵, Q = [ q 1 , ⋯ , q N ] \pmb{Q} = [\pmb{q}_1,\cdots,\pmb{q}_N] QQQ=[qqq1,⋯,qqqN], K = [ k 1 , ⋯ , k N ] \pmb{K} = [\pmb{k}_1,\cdots,\pmb{k}_N] KKK=[kkk1,⋯,kkkN], V = [ v 1 , ⋯ , v N ] \pmb{V} = [\pmb{v}_1,\cdots,\pmb{v}_N] VVV=[vvv1,⋯,vvvN]分别是由查询向量、键向量、值向量构成的矩阵。 - 对于每一个查询向量 q n ∈ Q \pmb{q}_n \in Q qqqn∈Q,利用键值对注意力机制,可以得到输出向量 h n \pmb{h}_n hhhn:
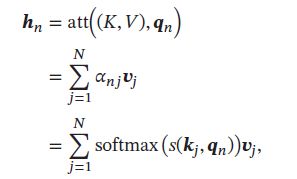
其中 n , j ∈ [ 1 , N ] n,j \in [1,N] n,j∈[1,N]为输出和输入向量序列的位置, α n j \alpha_{nj} αnj表示第 n 个输入关注到第 j 个输入的权重。
如果使用缩放点积为打分函数,输出向量序列可以简写为:
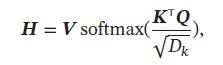
其中softmax为按列进行归一化的函数。
全连接模型和自注意力模型的对比如下,实线表示可学习的权重,虚线表示动态生成的权重,由于自注意力模型的权重是动态生成的,因此可处理变长的信息序列:
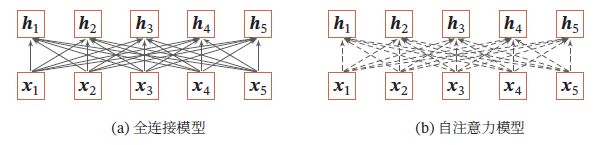
自注意力模型可作为神经网络中的一层使用,也可用来替换卷积层和循环层,也可以和他们一起交替使用(如X可以使卷积层或循环层的输出)。自注意力模型计算的权重 α i j \alpha_{ij} αij 只依赖于 q i \pmb{q}_i qqqi和 k j \pmb{k}_j kkkj的相关性,忽略了输入信息的位置信息。因此在单独使用时,自注意力模型可以拓展为多头自注意力模型(Multi-Head Self-Attention),在多个不同的投影空间中捕捉不同的交互信息。
4. 人脑中的记忆
生物神经网络中,记忆是外部信息在人脑中的存储机制。大脑记忆是通过生物神经网络实现的。直观上,记忆机制和神经网络的连接形态以及神经元的活动相关。整体效应存储在大脑中,记忆在大脑皮层是分布式存储的,而不是存储在某个局部区域。
人脑的记忆具有周期性和联想性。
记忆周期 人脑记忆特点,记忆分为长周期记忆、短周期记忆、长期记忆,也称为结构记忆或知识,体现为神经元之间的连接形态,其更新速度比较慢。短期记忆体现为神经元的活动,更新较快,维持时间为几秒至几分钟,是神经连接的暂时性强化,通过不断巩固、强化可形成长期记忆。短期记忆和长期记忆的动态更新过程为演化过程。
长期记忆类比于人工神经网络的权重参数,短期记忆类比于人工神经网络中的隐状态。
还有一个工作记忆,是人脑的缓存,维持时间常为几秒,与短期记忆不同:短期记忆一般指外界的输入信息在人脑中的表示和短期存储,不关心这些记忆如何被使用;而工作记忆是一个和任务相关的“容器”,可以临时存放和某项任务相关的短期记忆和其他相关的内在记忆. 工作记忆的容量比较小,一般可以容纳 4 组项目。
联想记忆 人脑一个主要特点是通过联想来进行检索的,联想记忆是指一种学习和记住不同对象关系的能力。
联想记忆指可通过内容匹配的方法进行寻址的信息存储方式,也称为基于内容寻址的存储,计算机是根据地址来进行存储的,叫随机访问存储。
和LSTM的记忆单元相比较,外部记忆可以存储更多的信息,并且不直接参与计算,通过读写接口来操作。因LSTM模型中的记忆单元包含信息存储和计算两功能,不能存储太多信息,故LSTM记忆单元像计算机寄存器,外部记忆像计算机内存单元。
借鉴人脑工作记忆,可在网络中引入一个外部记忆单元提高网络容量,外部记忆两种实现方式:1.结构化记忆,这种记忆和计算机中的信息存储方法类似,可分为多个记忆片段,并按一定的结构来存储;2. 基于神经动力学的联想记忆,具有更好的生物学解释性。
不严格记忆模型类比:
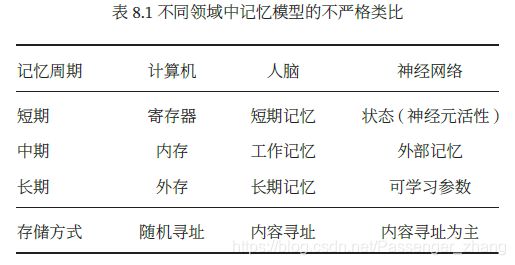
5. 记忆增强神经网络
为增强网络容量,引入辅助记忆单元,将和任务相关的信息保存在其中,需要时再读取。辅助记忆单元常称为外部记忆(External Memory),以区别RNN的内部记忆(隐状态),这种添加了外部记忆的神经网络也称作记忆增强神经网络(Memory Augmented Neural Network,MANN),或简称为记忆网络(Memory Network,MN)。
记忆网络主要有4个模块:
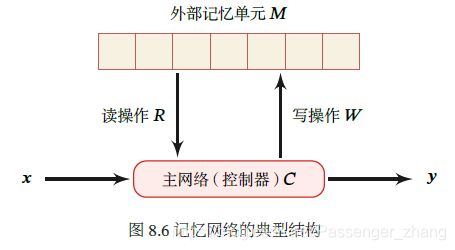
- 主网络C:也称为控制器(Controller),负责信息处理,并与外界的交互(接受外界输入,输出结果到外界)。主网络同时通过读写模块和外部记忆进行交互。
- 外部记忆单元M:外部记忆单元用来存储信息,一般可分为很多记忆片段,这些片段按一定结构组织,常用向量来表示,外部记忆单元可用一组向量 M = [ m 1 , ⋯ , m N ] \pmb{M} = [\pmb{m}_1,\cdots,\pmb{m}_N] MMM=[mmm1,⋯,mmmN] 表示。向量的组织方式可以是集合、树、栈、队列等。大部分信息存储在外部记忆中,不需全时参与主网络运算。
- 读取模块R:根据主网络生成的查询向量 q r \pmb{q}_r qqqr ,从外部记忆单元中读取相应的信息 r = R ( M , q r ) \pmb{r}=R(\pmb{M},\pmb{q}_r) rrr=R(MMM,qqqr)。
- 读取模块W:根据主网络生成的查询向量 q w \pmb{q}_w qqqw 和 要写入的信息 a \pmb{a} aaa 来更新外部记忆 M = W ( M , q w , a ) \pmb{M}=W(\pmb{M},\pmb{q}_w,\pmb{a}) MMM=W(MMM,qqqw,aaa)。
这种结构化的外部记忆是带有地址的,要实现人脑的联想记忆能力,需要按内容寻址的方式进行定位,然后进行读取或写入操作,按内容寻址通常使用注意力机制来进行。通过注意力机制可实现“软性”寻址方式,即计算一个在所有记忆片段上的分布,而不是一个单一的绝对地址。比如读取模型R的实现方式可以为:

其中 q r \pmb{q}_r qqqr 是主要网络生成的查询向量, s ( ) s() s()为打分函数,类比计算机存储器读取,计算注意力分布的过程类似计算机寻址过程,信息加权平均过程类似计算机内容读取过程。
引入外部记忆,可将神经网络的参数和记忆容量“分离”,即少量增加网络参数的条件下,可大幅增加网络容量,注意力机制可看做一个接口,将信息的存储与计算分离。外部记忆从记忆结构和读取方式等方面演变出很多模型。
5.1 端到端记忆网络
端到端记忆网络采用一种可微的网络结构,可多次从外部记忆读取信息,在端到端记忆网络中,外部记忆单元是只读的。
给定一组需要存储的信息 m 1 : N = { m 1 , ⋯ , m N } m_{1:N} = \{m_1,\cdots,m_N\} m1:N={ m1,⋯,mN} ,首先将其转换成两组记忆片段 A = [ a 1 , ⋯ , a N ] A = [\pmb{a}_1,\cdots,\pmb{a}_N] A=[aaa1,⋯,aaaN] 和 C = [ c 1 , ⋯ , c N ] C = [\pmb{c}_1,\cdots,\pmb{c}_N] C=[ccc1,⋯,cccN] 分别存放在两个外部记忆单元中,其中 A 用来寻址,C用来输出。
主网络根据输入 x \pmb{x} xxx 生成 q \pmb{q} qqq ,并使用键值对注意力机制来从外部记忆中读取相关信息 r \pmb{r} rrr:

并产生输出
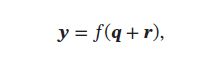
其中 f ( ) f() f()为预测函数,分类任务中, f ( ) f() f()可为Softmax函数。
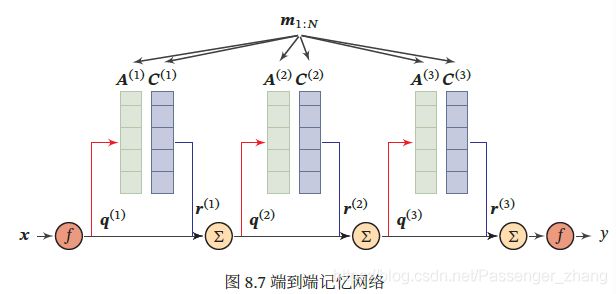
多跳操作 为了实现更复杂的计算,可让主网络和外部记忆进行多伦交互,在第 k 轮交互中,主网络根据上次从外部记忆中读取的信息 r ( k − 1 ) \pmb{r}^{(k-1)} rrr(k−1),产生新的查询向量:
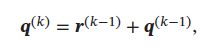
其中 q ( 0 ) \pmb{q}^{(0)} qqq(0) 为初始的查询向量, r ( 0 ) = 0 \pmb{r}^{(0)} = 0 rrr(0)=0。
假设第 k 轮交互的外部信息为 A ( k ) A^{(k)} A(k)、 C ( k ) C^{(k)} C(k),主网络从外部记忆读取信息为:
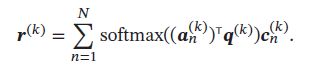
在第 K 轮交互后,用 y = f ( q ( K ) + r ( K ) ) \pmb{y} = f(\pmb{q}^{(K)} + \pmb{r}^{(K)} ) yyy=f(qqq(K)+rrr(K)) 进行预测。多轮的交互方式称为多跳(Multi-Hop)操作,该操作中参数共享,为简化起见,每轮交互的外部信息可共享使用,比如 A ( 1 ) = ⋯ = A ( K ) A^{(1)}=\cdots=A^{(K)} A(1)=⋯=A(K)、 C ( 1 ) = ⋯ = C ( K ) C^{(1)}=\cdots=C^{(K)} C(1)=⋯=C(K):
5.2 神经图灵机
- 无限长纸带:纸带少有一个个方格组成,每个方格可存储一个符号。
- 符号表:纸带上可能出现的所有符号的集合,包含一个特殊的空白符
- 读写头:指向纸带上某个方格的指针,每次可以向左或右移动一个位置,可对当前方格内容进行读写、擦除。
- 状态寄存器:用来保存图灵机当前所处的状态,其中包含两个特殊的状态:起始状态、终止状态
- 控制规则:根据当前机器所处的状态以及当前读写头所指的方格上的符号来确定读写头下一步的动作,令机器进入一个新的状态。
神经图灵机 主要由两个部件构成:控制器:一个前馈或循环圣经网络;外部记忆:定义为矩阵 M ∈ R D × N M \in \R^{D \times N} M∈RD×N,N 是记忆片段的数量,D是每个记忆片段的大小,可读写。
每个时刻 t ,控制器接受当前时刻的输入 x t \pmb{x}_t xxxt、上一个时刻的输出 h t − 1 \pmb{h}_{t-1} hhht−1、上一个时刻从外部记忆读取的信息 r t − 1 \pmb{r}_{t-1} rrrt−1,并产生输出 h t \pmb{h}_{t} hhht,同时生成和读写外部记忆相关的三个向量:查询向量 q t \pmb{q}_t qqqt、删除向量 e t \pmb{e}_t eeet、增加向量 a t \pmb{a}_t aaat 。然后对外部记忆 M t \pmb{M}_t MMMt 进行读写操作,生成读向量 r t \pmb{r}_t rrrt和新的外部记忆 M t + 1 \pmb{M}_{t+1} MMMt+1。
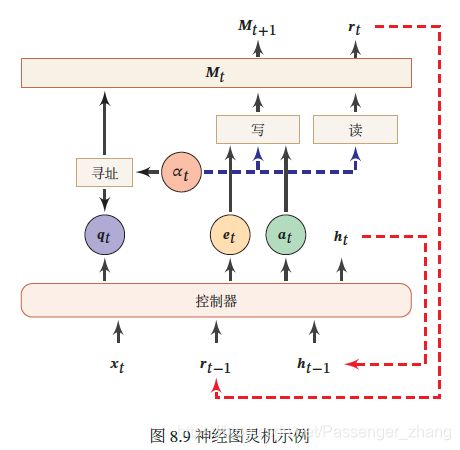
读操作 在时刻t,外部记忆的内容记为 M t = [ m t , 1 , ⋯ , m t , N ] \pmb{M}_t = [\pmb{m}_{t,1}, \cdots, \pmb{m}_{t,N}] MMMt=[mmmt,1,⋯,mmmt,N] ,读操作为从外部记忆 M t \pmb{M}_t MMMt 中读取信息 r t ∈ R D \pmb{r}_t \in \R^{D} rrrt∈RD。
首先通过注意力机制来进行基于内容的寻址,即:
![]()
其中 q t \pmb{q}_t qqqt 为控制器产生的查询向量,用来进行基于内容的寻址,函数 s()为加性或乘性的打分函数,注意力分布 α t , n \alpha_{t,n} αt,n 是记忆力片段 m t , n \pmb{m}_{t,n} mmmt,n 对应的权重,并满足 ∑ n = 1 N α t , n = 1 \sum_{n=1}^{N}\alpha_{t,n}=1 ∑n=1Nαt,n=1.
根据注意力分布 α t \alpha_t αt,可以计算读向量 r t \pmb{r}_t rrrt 作为下一个时刻控制器的输入:
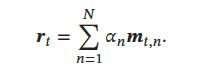
写操作 外部记忆的写操作可以分解为两个子操作:删除和增加。
控制器产生删除向量 e t \pmb{e}_t eeet 和增加向量 a t \pmb{a}_t aaat 分别为从外部记忆中删除的信息和增加的信息。删除操作是根据注意力分布来按比例地在每个记忆片段中删除 e t \pmb{e}_t eeet,增加操作是根据注意力分布来按比例地给每个记忆片段加入 α a t \alpha{a}_t αat。具体过程如下:
![]()
通过写操作得到下一个时刻的外部记忆 M t + 1 \pmb{M}_{t+1} MMMt+1。
6. 基于神经动力学的联想记忆
结构化的外部记忆更多是受现代计算机架构启发,分离计算和储存功能,缺乏生物学解释。基于神经动力学的联想记忆模型引入到神经网络增加网络容量,具有生物学可解释性。
联想记忆模型(Associative Memory Model)主要通过神经网络的动态演化来联想,两种应用场景:
- 输入模式和输出模式在同一空间,这种模型叫做自联想模型(Auto-Associative Model)。自联想模型可以通过前馈神经网络或RNN来实现,也常称为自编码器(Auto-Encoder,AE)。
- 输入模式和输出模式不在同一空间,这种模型叫做异联想模型(Hetero-Associative Model)。广义上讲,大部分机器学习问题都可看做异联想,因此异联想模型可作为分类器使用。
联想记忆模型可以成一种RNN,基于神经动力学来实现按内容寻址的信息存储和检索。
6.1 Hopfield网络
除作为机器学习模型外,神经网络还可以作为一种记忆的存储和检索模型。
Hopfield 网络(Hopfield Network)是一种RNN网络,由一组相互连接的神经元组成,Hopfield 网络也可认为是所有神经元都相互连接的不分层的网络,每个神经元既是输入单元,又是输出单元,没有隐藏神经元。一个神经元和自身没有反馈相连,不同神经元之间连接权重是对称的。
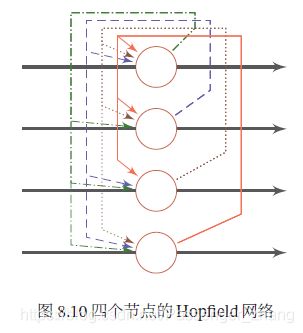
假设一个Hopfield 网络有M个神经元,第 i 个神经元的更新规则为:

其中 w i j w_{ij} wij 为神经元 i 和 j 之间的连接权重, b i b_i bi为偏置。
连接权重 w i j w_{ij} wij 有以下性质:
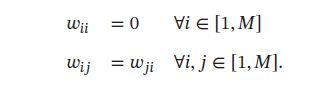
Hopfield 网络更新可分为异步和同步两种方式,异步更新是每次更新一个神经元,更新顺序可以是随机或事先固定的;同步更新是指一次更新所有的神经元,需要有一个时钟来进行同步,第 t 时刻的神经元状态 s t = [ s t , 1 , ⋯ , s t , M ] T \pmb{s}_t = [s_{t,1},\cdots,s_{t,M}]^T ssst=[st,1,⋯,st,M]T ,其更新规则为:
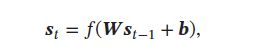
其中 s 0 = x , W = [ w i j ] M × M \pmb{s}_0 = \pmb{x}, \pmb{W}=[w_{ij}]_{M \times M} sss0=xxx,WWW=[wij]M×M 为连接权重, b = [ b i ] M × 1 \pmb{b} = [b_i]_{M \times 1} bbb=[bi]M×1 为偏置向量,f 为非线性阶跃函数。
能量函数 在Hopfield中,每个不同的网络状态定义为一个标量属性,称为能量

Hopfield网络是稳定的,即能量函数经过多次迭代后会达到收敛状态,权重对称是一个重要特征,因为他保证能量函数在神经元激活时单调递减,不对称的权重可能导致周期性震荡或混乱。
给定外部输入,网络经过演化,会达到某个稳定状态,这些稳定状态称为吸引点(Attractor),一个Hopfield中常有多有吸引点,每个吸引点为一个能量的局部最优点。下图红线为网络能量的演化方向,蓝点为吸引点:
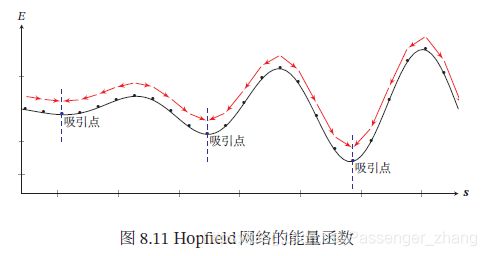
联想记忆 Hopfield网络存在有限的吸引点,每个吸引点 u 都对应一个“管辖”区域 R u R_u Ru ,如果输入向量 x \pmb{x} xxx 落入这个区域,挽留过最终会收敛到 u。因此,吸引点可以看做是网络中存储的模式,将输入 x \pmb{x} xxx 作为起始状态,随时间收敛到吸引点 u \pmb{u} uuu 上的过程为检索过程。即使输入向量 x \pmb{x} xxx 只包含部分信息或包含噪声,,只要其位于对应存储模式的“吸引”区域内,那么随着时间演化,网络最终会收敛到其对应的存储模式. 因此,Hopfield 的检索是基于内容寻址的检索,具有联想记忆能力。
信息存储 信息存储是指将一组向量 x 1 , ⋯ , x N \pmb{x}_1,\cdots,\pmb{x}_N xxx1,⋯,xxxN 存储在网络中的过程,存储过程主要调整神经元之间的连接权重,故可以看作是一种学习过程。Hopfield 网络的学习规则有很多种. 一种最简单的学习方式为:神经元 和 之间的连接权重通过下面公式得到:
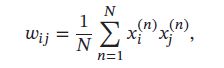
如果 x i x_i xi 和 x j x_j xj 在输入向量中相同的概率越多,则 w i j w_{ij} wij越大。这种学习规则类似人脑神经网络的学习:如果两个神经元经常同时被激活,则连接加强,否则连接消失。这种学习方式称为Hebbian 法则。
存储容量 对于联想记忆模型来说,存储容量为其能够可靠地存储和检索模式的最大数量。对于数量为 M 的互相连接的二值神经元,总状态数 2 M 2^M 2M,其中可作为有效稳定点的状态数量就是其存储容量。模型容量一般与网络结构和学习方式有关。Hopfield网络最大容量为 0.14M,玻尔兹曼机的容量为0.6M,但是其学习效率低,需要长时间的演化才能到达均衡状态。通过改进学习算法,Hopfield网络的最大容量可以到达 O(M)。如果允许高阶(K)连接,比如三个神经元连接关系,其稳定存储的最大容量 O ( M K − 1 ) O(M^{K-1}) O(MK−1) 。引入复数运算,有效提高了网络容量,总体上讲,通过改进网络结构、学习方式、引入更复杂的运算(复数、量子操作),可有效改善联系记忆网络的容量。
6.2 使用联想记忆增加网络容量
联想记忆具有存储和检索功能,我们可以利用联想记忆来增加网络容量。和结构化的外部记忆相比,联想记忆具有更好的生物学解释性。如,将一个联想记忆模型作为部件加入LSTM网络,从而在不引入额外参数的情况下增加网络容量,或者将RNN网络中的部分连接权重作为短期记忆,并通过联想记忆模型进行更新,从而提高网络性能。上述网络中,联想记忆都是作为一个更大网络的组件,用来增加短期记忆的容量。联想记忆组件的参数可以使用Hebbian 方式来学习,也可以作为整个网络参数的一部分来学习。
