理解深度学习中的“卷积神经网络”

博主最近在学习YOLO系列算法，本文是博主学习后的笔记，详细介绍了卷积，希望能帮助到入门深度学习和卷积网络的童鞋。
声明：本文用到的部分材料来自吴恩达老师的《深度学习》和51CTO小超老师的 “YOLOV4代码复现-—行人车辆检测”课程。

卷积介绍

二维卷积

假设：
这里我们假设3种网格，对应3个矩阵。

假设我们有一张7×7的输入图片，在计算机中，就是一个7×7的矩阵，记为A。同时，假设我们人为构建了另一个3×3的矩阵。这个3×3的矩阵，就是卷积中的过滤器（filter），也称作卷积核（kernal）。最后，假设有一个空的矩阵，存放卷积结果，记为B。

操作：
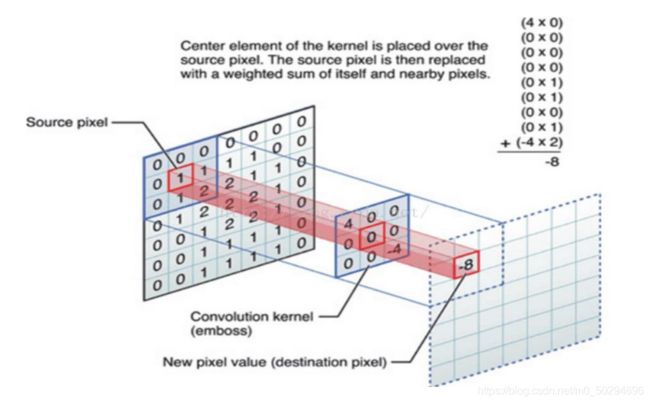
（1）对7×7的原始图像进行卷积操作时，我们先从左上角开始，圈定一个和卷积核同样大小的区域，这里就是3×3，然后将此区域单独拿出，和卷积核执行一个类似点乘的操作，将它们对应位置的元素分别相乘。乘完之后，将得到的9个数值相加，会生成一个新的数。而这个数值，就是我们得到的新的特征值。在下图中，这个新的特征值就是-8。
将新特征值-8填入存放卷积结果的空矩阵中，对应第一行第一列，即B[0][0]的位置。

（2）在原图中，记水平为x，竖直为y。将原图中被圈定执行卷积的区域向右挪一步，即y保持不变，x向右移动一个单位。在下图中，圈定的9个数就从000 011 012 变为 000 111 122。对这个区域重复执行卷积操作，即与卷积核对应位置元素点乘后相加，得到新的特征数，算出后也是-8。将其填入矩阵B的第一行第二列，B[0][1]。

（3）不断重复上述步骤，对x方向操作完后y方向下移一格，重复操作，直到卷积的区域一直移到右下角。最终生成的C就是一个5×5的矩阵。即原本7×7的图像，经过了3×3的卷积核后，生成了新的5×5的特征图。
当然这个参数都是可变的，原始图像的图像可能不是7×7，而是608×608甚至更大，而卷积核常见的有1×1,3×3和5×5。

三维卷积

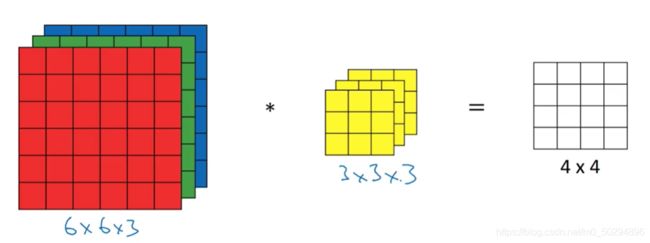
我们需要处理的图像多数情况下并不是灰度图，可以用二维矩阵模拟，而是彩色图。假设输入图像是RGB形式，那么一个图像就有3个通道，分别对应红色，绿色和蓝色。每个通道都对应单独的一个输入矩阵。

如图所示，输入有3个通道，因此相对应的，卷积核也需要3个通道。在具体卷积时，核的第一层与红色卷积，第二层与绿色卷积，第三层与蓝色卷积，每一层都输出9个数，一共27个数。值得注意的是，在进行三维卷积时，并不是红色部分单独卷，单独输出，而是三个通道一起卷积，最终的输出是一个特征值，这个特征值是27个数值相加得到。

因此，在3维卷积中，输入是3维，卷积核是3维，但输出是2维的。

这是单个卷积核所用的结果。如果不只有一个卷积核，而是2个卷积核。那么将对每个卷积核重复上述步骤，得到一个2维输出，最终得到2个二维输出，将这2个输出拼接起来，就是一个3维的新特征输出。在本例中，为4×4×2。

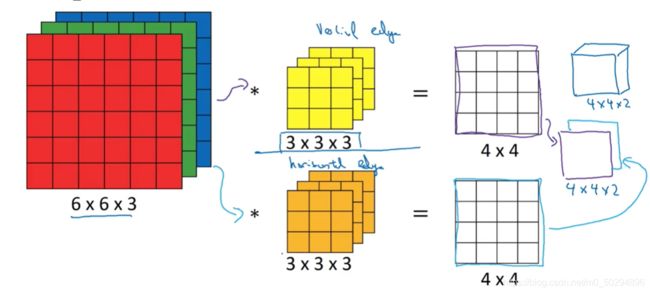
在三维卷积中，卷积核的通道数必须与输入的通道数相等，而输出的通道数就是卷积核的数量。

卷积核

在深度学习中，卷积核的尺寸是人为设定的，比如3×3，或者5×5。而里面具体的数则有所不同，可以人为设定，即人工卷积核，也可以通过神经网络学习得到。

人工卷积核的特点:
上文中二维卷积假设的卷积核，左上角是4，右下角是-4，其他区域都是0，这表明此卷积核只关注图像中被圈定部分的左上角和右下角，其权重分别是4和-4，其他地方不关注。

下图展现了另外两种卷积核，分别能达到检测图像垂直边缘和水平边缘的作用。详细可以参考吴恩达老师的深度学习课程中垂直检测的部分。

下图中的卷积核只有中间有数值，且权重为1，作用于原图后最终输出和原图的区别只是少了最外面的一圈像素，其他地方不变。

下图中的卷积核中间数值最大，而其余部分很小，卷积后的结果非常突出中间部分，锐化图像。

此外，通过设置整齐的（0,1）之间的参数，比如都为0.2，有均值模糊的作用。美颜软件应用较多，可以达到光滑肌肤的作用。

当然，更常见的情况是，不设置卷积核中具体的参数，而是只给它一个尺寸，里面具体的参数则放到神经网络中，让它自己学习。

为什么要使用卷积？（ 卷积核与全连接层的关系）

下面是一个简单的全连接层的神经网络

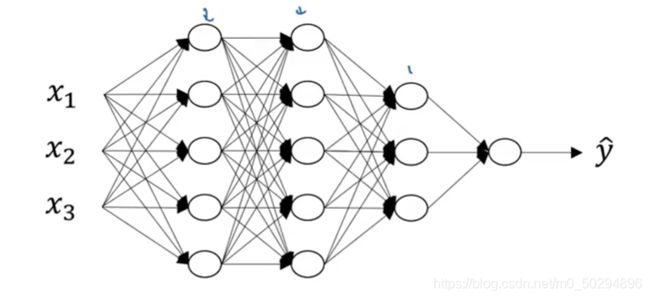
这个神经网络非常小，输入只有3个特征值，$x_1,x_2$和$x_3$。而且神经网络只有4层，非常浅。而在上文中，即使我们的输入图像也很小，只有7×7，那也有49个输入特征，如果是1000×1000的图像呢？如果神经网络有几十层呢？那么可想而知，需要学习的参数将非常多，一般计算机的计算能力远远达不到要求。

同时，全连接层的每一个神经元都是前一层网络经过权重计算得到，对于图像来说，这种操作会损失图像的空间信息，不利于目标检测的任务。

基于以上两个原因，卷积核被应用到神经网络中，卷积核只关注部分信息。举例来讲，在上文-8的输出特征中，只是卷积核和原图中左上角的9个特征输入做了计算，而其他地方的特征值则没有参与。相当于将全连接层人为拆开。

对7×7的输入图像，如果用全连接层，假设第一层神经网络的神经元个数为50，权重参数有50×49约有2500个（如何理解权重：数数上图中$x_1,x_2$和$x_3$到第一层的那5个鸡蛋中间是不是有5×3=15条连线？）。而如果用10个3×3的卷积核，则参数只有90个。参数缩减效果十分明显。所以在很多模型中，比如YOLOv4，使用了全卷积网络，在保留空间信息同时，极大缩减了学习参数的数量。

如果设计的卷积核足够大，和输入图像一样大，也是7×7，那么只能对原图做一次卷积操作，这个输出和原图所有特征都有关，相当于全连接层。

所以，全连接层相当于对全图做了卷积运算。

---

关于卷积的其他操作，如步长，池化，padding等，请持续关注博主，不日将继续更新。

如果觉得有帮助，欢迎点赞+收藏，笔芯~