【论文翻译】（NIPS2018）Flexible Neural Representation for Physics Prediction 物理预测的灵活神经表示

译者：子鱼
论文地址：https://arxiv.org/pdf/1806.08047.pdf
源码和更多材料：https://neuroailab.github.io/physics/
参考文献和补充材料请见原文。译者水平有限，错误难免，恳请读者批评指正。译者目前正在做这个方向的研究，欢迎读者与我交流，可博客留言或发邮件至[email protected]

摘要

人类有一种非凡的能力来理解其环境中物体的物理动力学，灵活地捕捉多个细节水平上的复杂结构和相互作用。受到这种能力的启发，我们提出了一种层次化基于粒子的对象表示，它涵盖了各种各样的三维物体，包括任意刚性几何形状和可变形材料。然后我们描述了层次关系网络(Hierarchical Relation Network, HRN)，这是一种基于层次化图卷积的端到端可微神经网络，它学习在这种表示中预测物理动力学。与其他神经网络基准方法相比，HRN精确地处理复杂的碰撞和非刚性变形，在新设置中在长时间尺度下生成可信的动力学预测，并缩放到大型场景配置。这些结果展示了一种架构，它有可能成为在计算机视觉、机器人和量化认知科学中使用的下一代物理预测器的基础。

1 介绍

人类有效地将环境分解为物体，并有效地推理这些物体之间的动态交互作用[43,45]。虽然在某些情况下，人类的直觉物理在定量上可能是不准确的，但是，人类对他们的环境在很长一段时间内的动态轨迹做出了定性的可信的的猜测。此外，他们要么生来就知道，要么很快就学会了一些概念，比如客体永久性、遮挡关系和可变形性，这些概念指导着他们的感知和推理[42]。

能够模仿这种能力的人工系统将在计算机视觉、机器人技术、强化学习和许多其他领域的应用中发挥巨大作用。虽然传统的为计算机图形构造的物理引擎已经取得了很大的进步，但这些程序通常是硬连接的，因此很难被集成为更大的可学习系统的组件。因此，为物理预测创建端到端可微的神经网络是一个吸引人的想法。最近，Chang等人[11]和Battaglia等人[4]通过提出以对象为中心和以关系为中心的表示，展示了在(大部分)2D场景中使用神经网络来预测物理对象交互的方法。这些作品的共同之处是将场景处理为图，用节点表示对象点集，用边描述对象之间的成对关系(如引力、弹力或排斥关系)。利用物体的关系和物理状态来计算物体之间的成对效应。将对一个物体的影响结合起来，就可以在每个物体的基础上预测未来环境的物理状态。这种方法在显式处理对象交互的能力方面非常有前途。然而，在将这种方法推广到真实世界的物理动力学方面仍然存在许多挑战，包括以足够的分辨率表示任意几何形状以捕获复杂碰撞，同时处理不同尺度的对象，以及处理具有复杂程度的非刚性对象。

图1： 预测物理动力学。 任务是根据过去的观察预测一个系统未来的物理状态。在这个例子中，立方体在与地面碰撞时发生变形。上面一行显示的是真实位置，下面一行显示的是我们的物理预测网络的预测。

图1所示的快速移动变形立方体序列说明了其中几个挑战。人类可以灵活地改变他们感知这些运动物体的细节水平：立方体可以自然地被认为是一个不可分的质点，因为它沿着初始运动轨迹移动。但当它与地面碰撞并从地面弹起时，立方体复杂的直线子结构和非刚性材料特性对于理解发生了什么以及预测未来的相互作用变得非常重要。人类大脑如何轻松地处理如此复杂的场景是认知科学的一个重要的待研究问题，也是人工智能面临的一个关键挑战。在这两个目标的激励下，我们的目标是开发一种新型的神经网络结构，它具有类似人类的能力，可以灵活地对物理世界进行推理。

为此，通过将每个对象表示为一个(可能很大的)连接粒子的集合来扩展交互网络框架是很自然的。在这样的表示中，单个组成粒子可以独立运动，允许物体变形，同时受到防止物体分裂的成对关系的约束。然而，这种基于粒子的表示方式本身就带来了许多挑战。从概念上讲，目前还不清楚如何有效地在这样一个对象中传播一种效应。此外，用成百上千个粒子来表示每一个物体会导致大量的成对关系，这在计算上是不可行的，在认知上也是不自然的。

为解决这些问题，我们提出一个新颖的受认知启发的基于图的层次性对象表示来描述各种复杂的刚性和可变形的物体(第3节)，和一个有效的层次化图卷积神经网络来学习这个表示中的物理预测(第4节)。对于评估复杂的3D场景，我们显示了相较于很强的基准方法的实质性改进，无论是在定量预测精度和定性预测可信度，以及对复杂的未见过的场景的泛化的证据(第5节)的方面。

2 相关工作

高效、灵活的物理动力学预测器一直是神经网络设计中的一个突出问题。在计算机视觉中，为了识别运动而给图像和视频中的运动物体建模，未来预测和目标追踪是非常值得关注的方法。在机器人技术中也是如此，从图像中预测未来的动作情况对于导航或物体交互是至关重要的。然而，直接在二维图像表示上操作的未来预测器常常无法生成清晰的物体边界，且难以处理在物体不再可见时的遮挡关系和物体位置记忆[1,17,16,28,29,33,34,19]。使用3D卷积或点云的表示可以更好地保持物体的形状[46,47,10,36,37]，但不能完全捕捉客体永久性，而且计算效率低。与我们的方法更类似的是逆图形方法，它从用于预测物理的图像中提取出较低维的物理表示[25, 26, 51, 50, 52, 53, 7, 49]。我们的工作借鉴并扩展了Chang等人[11]和Battaglia等人[4]的工作，他们反过来使用了基于图的神经网络的思想[39,44,9,30,22,14,13,24,8,40]。然而，现有的大部分工作并不能自然地处理具有大尺度变化的物体的复杂场景，或者具有复杂材质的可变形物体。

物理模拟在计算机图形学中也有很长时间的研究，最常见的是刚体碰撞[2,12]。粒子或点集也被用来代表更复杂的物理对象，以神经网络为基础的NeuroAnimator（神经动画）是最早使用对象的层次化粒子表示，以提升物理对象的运动效果[18]的例子之一。我们基于粒子的对象表示也从最近的(非神经网络)物理模拟工作中获得灵感，特别是NVIDIA FleX引擎[31,6]。然而，与这项工作不同的是，我们的解决方案是一个端到端可微分的神经网络，可以从数据中学习。

最近计算认知科学的研究假设，人类在大脑中进行物理模拟[5,3,20,48,21]。这似乎是合理的，这样的模拟发生在正确的细节水平，可以灵活地适应需要，与我们提出的表示方式类似。当将人的技能推广到新环境或灵活地适应输入和目标[27]的变化时，想象物体运动的能力以及灵活地将环境分解为物体和组块的能力是人类进一步学习新任务的重要先验能力。

3 层次化粒子图表示

（译者注——345节描述的方法很复杂，英文原文表述很生动，但是由于译者中文太烂实在翻译不出来，用了很多机翻，因此还是建议大家阅读原文，译文仅供参考）

预测系统未来物理状态的一个关键因素是所使用的底层表示方式。一个简化但严格的假设是所有对象都是刚性的。刚体可以用一个质点表示，并通过指定其位置和方向明确地在空间中定位，同时用单独的数据结构描述物体的形状和范围。例如3D多边形网格或从感知数据中提取的各种形式的2D或3D遮罩[10,16]。刚体假设只描述了现实世界的一小部分，不包括柔软的物体、布料、流体和气体，也不包括物体的断裂和结合。然而，对象是可分割的，并且可能由大量较小的子部分组成。

给定一个场景和一组对象$O$,核心观点是代表每个对象$o\in O$与一组粒子 $P_o\equiv \{p_i|i\in o\}$ 。每个粒子在t时刻的状态由${\mathbb{R}}^7$中的一个矢量描述由它的位置$x\in {\mathbb{R}}^3$，速度$\delta \in {\mathbb{R}}^3$，质量$m\in {\mathbb{R}}^{+}$。我们交替地引用$p_i$和这个向量。

粒子在一个物体上分散开来以充分描述它的体积。理论上，粒子可以被任意放置在物体内部。因此，复杂程度较低的零件可以用较少的粒子来描述(例如，8个粒子完全定义一个立方体)。更复杂的零件(如长杆)可以用更多的粒子来表示。我们定义$P$为这个集合$\{p_i|1\le i\le N_P\}$包含观察场景中所有$N_P$个粒子。

图2:基于图的层次化粒子表示。物体被分解成粒子。(相同颜色的)粒子被分组到一个层次，整体上代表多个尺度的物体结构。成对关系约束同一类群中的粒子，并约束它们的祖先节点和子节点。

为了完整地在物理上描述多个包含粒子的物体的场景，我们还需要定义粒子之间是如何相互关联的。与Battaglia等人[4]相似，我们用K维两两关系$R=\{r_{ij}\in {\mathbb{R}}^K\}$来表示粒子$p_i$和$p_j$之间的关系。对象内的每个关系$r_{ij}$编码材质属性。例如，对于一个软体，$r_{ij}\in \mathbb{R}$表示局部材料的刚度，它不必在一个物体内是均匀的。具有潜在非均匀材料的任意形状的物体可以用这种方式表示。请注意，$r_{ij}$的物理解释是从数据中获得的，而不是通过硬编码的方程。总的来说，我们用一个节点带标签的图$G=⟨P,R⟩$来表示场景，其中粒子组成了节点$P$，关系定义了(有向)边$R$。除了碰撞的情况下，在$G$中不同的物体是不相连的组件。

图$G$用于在场景中传播(外界施加的)影响。由于两两关系计算复杂度为$\mathcal{O}(N_P^2)$，使用完全连通图进行传播是不可行的。为了实现$\mathcal{O}(N_P\log (N_P))$复杂度，我们从$G$构造层次化场景(有向)图$G_H$，其中每个连通组件的节点被组织成树形结构：首先将$G_H$中的叶节点$L$初始化为原始粒子集合$P$，然后给$G_H$扩展一个表示$G$中每个连通组件(对象)的根节点，根节点状态定义为其叶节点状态的集合。根节点与叶节点之间用有向边双向连接。

此时，$G_H$由代表最优场景分辨率的叶子粒子$L$和在物体层次上描述场景的每个连接组件的一个根节点组成。为了获得中间层次的细节，我们然后使用改进的k-means算法将每个连接组件中的叶子$L$聚类到更小的子组件中。我们为每个新子组件添加一个节点，并将其叶子连接到新添加的节点，反之亦然。然后，这个新添加的节点被标记为它的叶子的直接祖先，它的叶子是彼此的兄弟。然后，当且仅当它们各自的子组件叶子连接起来时，我们将添加的中间节点彼此连接起来。最后，我们从每个连接组件的根节点向该组件的新中间节点添加有向边，并删除不属于同一簇的叶子之间的边。然后，这个过程在每个新的子组件中递归。详见附录中的算法1。

我们用sib($p$)来表示粒子$p$的兄弟节点(们)，用anc($p$)来表示它的祖先节点(们)，用par($p$)来表示它的父节点，用des($p$)来表示它的后代节点(们)。我们定义了leaves$(p_a)=\{p_l\in L|p_a\in \text{anc}(p_l)\}$。注意，在$G_H$中，有向边连接$p_i$和sib($p_i$)，叶$p_l$和anc($p_l$)， $p_i$和des($p_i$);参见图3b。

4 物理预测模型

在这一节中，我们将介绍我们的物理预测模型。它基于层次化图卷积，这是一种通过图的层次传播相关物理效应的操作。

4.1 层次化图卷积用于传播影响

为了预测未来的物理状态，我们需要解决在层次图中连接的粒子对彼此施加的约束。我们使用图卷积来计算和传播这些影响。在Battaglia等人[4]的基础上，我们使用两个基本构件实现了一个两两图卷积：(1)一个两两处理单元$\varphi$,需要发送粒子状态$p_s$,接收粒子状态$p_r$的和它们的关系$r_{sr}$作为输入和输出的影响$e_{sr}\in {\mathbb{R}}^E$，和(2)可交换的聚合运算$\Sigma$收集和计算整体影响$e_r\in {\mathbb{R}}^E$。在我们的例子中，这是对$p_r$的所有影响的简单求和。这两个构件形成一个图上的卷积，如图3所示。
图3：通过图卷积传播影响。a)两两图卷积 $\varphi$。通过与发送粒子$p_s$的图关系$r_{sr}$约束接收粒子$p_r$的运动。给定$p_s$、$p_r$和$r_{sr}$，利用全连接神经网络计算$p_s$对$p_r$的影响的$e_{sr}$。整体影响$e_r$为对$p_r$的所有影响之和。b)层次化图卷积$\eta$ 。层次结构中的影响通过三个连续的步骤传播。(1)${\varphi }_{L2A}$。叶子粒子$L$向其祖先$A$传播影响(2)${\varphi }_{WS}$影响在兄弟粒子$S$之间交换。(3)${\varphi }_{A2D}$。影响从祖先$A$传播到他们所有的后代$D$。

两两处理限制了图卷积只能在直接连接的节点之间传播影响。对于一般的平面图，我们必须重复应用这个操作，直到来自所有粒子的信息传遍整个图。这在有许多粒子的情况下是不可行的。相反，我们利用粒子和它们在层次结构中的祖先之间的直接连接，在一个模型步骤中传播整个图的所有影响。我们引入了一种层次图卷积，这是一种传播影响的三阶段机制，如图3b所示。

第一L2A(Leaves To Ancestors, 叶子到祖先)阶段${\varphi }^{L2A}(p_l,p_a,r_{la},e_l^0)$预测对给定的$p_l,p_a$，一个叶子粒子$p_l$对祖先粒子$p_a\in \text{anc}(p_l)$的影响$e_{la}^{L2A}\in {\mathbb{R}}^E$。第二WS(Within Siblings, 兄弟之间)阶段${\varphi }^{WS}(p_i,p_j,r_{ij},e_i^{L2A})$预测一个粒子$p_i$对兄弟粒子$p_j\in \text{sib}(p_i)$的影响$e_{ij}^{WS}\in {\mathbb{R}}^E$。第三A2D(Ancestors to Descendants, 祖先到后代)阶段${\varphi }^{A2D}(p_a,p_d,r_{ad},e_a^{L2A}+e_a^{WS})$预测一个祖先粒子$p_a$对后代粒子$p_d\in \text{des}(p_a)$的影响$e_{ij}^{A2D}\in {\mathbb{R}}^E$。粒子$p_i$受到的总影响$e_i$是各种影响的求和$e_i=e_i^{L2A}+e_i^{WS}+e_i^{A2D}$，其中：

$$\begin{gathered} e_a^{L2A}=\sum _{p_l\in \text{leaves}(p_a)}{\varphi }^{L2A}(p_l,p_a,r_{la},e_l^0) \\ {e}_j^{WS}=\sum _{p_i\in \text{sib}(p_j)}{\varphi }^{WS}(p_i,p_j,r_{ij},e_i^{L2A}) \\ {e}_d^{A2D}=\sum _{p_a\in \text{anc}(p_d)}{\varphi }^{A2D}(p_a,p_d,r_{ad},e_a^{L2A}+e_a^{WS}) \end{gathered}$$

实际上，${\varphi }^{L2A}$，${\varphi }^{WS}$，${\varphi }^{A2D}$被实现为共享权值的全连通网络，它们以one-hot向量的形式接收额外的三元输入(L2A为0,WS为1,A2D为2)。

由于一个对象中的所有粒子都连接到根节点，信息可以在至多两个传播步骤中在整个层次图中流动。我们在模型中使用了这个属性。

4.2 层次化关系网络结构

本节介绍层次关系网络(HRN)，这是一种用于预测未来物理状态的神经网络，如图4所示。在每一个时间步t上，HRN以层次场景图$G_H^{(t-T,t]}$的形式，取T之前历史的粒子状态$P^{(t-T,t]}$和关系$R^{(t-T,t]}$作为输入。$G_H^{(t-T,t]}$随时间动态变化，为足够接近的粒子对添加了定向的无标记虚拟碰撞关系。HRN还会接受对系统产生的外部影响(例如重力g或外力F)作为输入。该模型由三个成对的图卷积模块组成，一个用于外力${\varphi }_F$，一个用于碰撞${\varphi }_C$，还有一个用于过去状态${\varphi }_H$，后面连着层次化图卷积模块$\eta$用于在粒子中分层传播影响。最后全连接模块$\psi$输出下一个状态$P^{t+1}$。

图4:层次关系网络。该模型取过去的粒子图$G_H^{(t-T,t]}=⟨P^{(t-T,t]},R^{(t-T,t]}⟩$作为输入输出下一个状态$P^{t+1}$。每个图卷积影响模块$\varphi$的输入是粒子的状态和关系，输出是各自的影响。${\varphi }_H$处理过去的状态，${\varphi }_C$碰撞和${\varphi }_F$外力。分层图卷积模块$\eta$对所有两两粒子状态、关系和影响求和，并传播给整个图。最后，$\psi$利用传播的影响计算下一个粒子的状态$P^{t+1}$

下面，我们将简要介绍每个模块。为了便于阅读，我们省略了符号$(t-T,t]$，并假设所有变量都服从这个时间范围，除非另有说明。

外力模块 ${\varphi }_F$将作用在叶子粒子$p_i\in P^L$上的力$F\equiv f_i$转化为影响${\varphi }_F(p_i,f_i)=e_i^F\in {\mathbb{R}}^E$。

碰撞模块 两个物体之间的碰撞被动态定义为来自一个物体的叶子粒子$p_i\in P^L$与来自另一个与之相靠近的物体的叶子粒子$p_j\in P^L$之间的两两碰撞关系$r_{ij}^C$[11]。 碰撞模块${\varphi }_C$使用$p_i$,$p_j$和$r_{ij}^C$来计算$p_j$对$p_i$的影响${\varphi }_C(p_j,p_i,r_{ij}^C)=e_{ji}^C\in {\mathbb{R}}^E$，反之亦然。设$d^t(i,j)=||x_i^t-x_j^t||$，总碰撞影响$e_i^C={\sum }_j\{e_{ji}|d^t(i,j)<D_C\}$。超参数$D_C$表示碰撞关系中的最大距离。

历史模块 ${\varphi }_H$预测了历史$p_i^{(t-T,t-1]}\in P_L$对当前叶子粒子状态$p_i^t\in P_L$的影响${\varphi }_H(p_i^{(t-T,t-1]},p_i^t)=e_i^H\in {\mathbb{R}}^E$(原文是$\in e_i^H$，疑有误——译者注)。

层次化影响传播模块 $\eta$传播总影响$e_i^0=e_i^F+e_i^C+e_i^H$。$\eta$对应于图3b中的三阶段层次化图卷积，给定成对粒子$p_i$,$p_j$的状态，它们的关系$r_{ij}$和输入影响$e_i^0$，输出在每个粒子$p_i$上被传播的总影响$e_i$。

状态预测模块 我们使用一个简单全连接网络$\psi$来预测粒子的下一个状态$P_{t+1}$。为了得到更准确的预测，我们利用了层次化粒子表示法，通过在以父节点为原点的局部坐标系中预测任何给定粒子的动力学。唯一的例外是用于预测整体动力学的物体根节点粒子。具体来说，就是状态预测模块$\psi (g,p_i,e_i)$利用粒子状态$p_i$、在$p_i$上的总影响$e_i$和重力$g$作为输入来预测未来的局部位移${\delta }_{i,l}^{t+1}={\delta }_i^{t+1}-{\delta }_{\text{par}(i)}^{t+1}$。由于我们只预测物体根节点粒子的整体动力学，重力只适用于这些根节点粒子。最终的在世界坐标中的未来位移根据局部信息计算，${\delta }_i^{t+1}={\delta }_{i,l}^{t+1}+{\sum }_j{\delta }_{j,l}^{t+1},j\in \text{anc}(i)$。

4.3 通过损失函数和数据学习物理约束

传统上，物理系统是用为真实世界提供固定近似的方程来建模的。相反，我们选择从数据中学习物理约束，包括物质属性向量的含义。我们发现最有效的误差信号是三个目标的组合。(1)我们独立地预测时间步t到t+1时层次中所有粒子的位置变化${\delta }_{i,l}^{t+1}$。实际上，我们发现大小不同的粒子的${\delta }_{i,l}^{t+1}$在不同的量级。因此，我们利用同一体积水平上所有粒子的统计量对局部动力学进行归一化(local loss，本地损失)。(2)我们还要求整体未来位移${\delta }_i^{t+1}$是准确的(global loss, 整体损失)。(3)我们的目标是通过使相互连接的的两个粒子$p_i$和$p_j$在下一个时间步$d^{t+1}(i,j)$中成对的距离与真实位置匹配来保持物体内粒子的结构。在刚体的情况下，这一项起作用，以保持粒子之间的距离。对于软体，这个目标确保正确地学习成对的局部变形(preservation loss, 保形损失)。

总目标函数线性地组合(1)、(2)和(3)，用超参数$\alpha$和$\beta$加权：
$$Loss=\alpha \left(\sum _{p_i}||{\hat{\delta }}_{i,j}^{t+1}-{\delta }_{i,j}^{t+1}|{|}^2+\beta \sum _{p_i}||{\hat{\delta }}_i^{t+1}-{\delta }_i^{t+1}|{|}^2\right)+(1-\alpha )\sum _{p_i\in \text{sib}(p_j)}||{\hat{d}}^{t+1}(i,j)-d^{t+1}(i,j)|{|}^2$$

5 实验

在本节中，我们将研究HRN在刚体、可变形体(软体、布料和流体)、碰撞和外部动作场景中准确预测随时间变化的物理状态的能力。我们还评估了不同对象和环境属性的泛化性能。最后，我们展示了一些更复杂的场景，包括(例如)倒塌的积木塔和多米诺骨牌。预测转出是通过递归反馈HRN的一步预测作为输入来产生的。我们强烈建议读者查看主要文本图、补充材料中显示的结果示例，并访问https://youtu.be/kD2U6lghyUE。

下面实验的所有训练数据都是通过Unity3D中基于FleX物理引擎[31]的自定义交互式粒子环境生成的。该环境提供了(1)一种自动提取三维物体网格粒子表示的方法，(2)一种生成随机物理场景用于生成静态训练数据的方便方法，(3)一种通过力与环境中的物体交互的标准化方法。关于实验设置和训练程序的进一步细节可以在补充材料中找到。

5.1 物理现象的定量评估

**刚体的运动和外力。**在第一个实验中，通过外力的作用，刚性物体被从地面向上推，然后下落并与地面相撞。模型训练10种不同的简单形状(立方体、球体、金字塔、圆柱、长方体、圆环、棱柱、八面体、椭球体、平面金字塔)，每个有50-300个粒子。静态平面是用5000个具有几乎无限质量的粒子来表示的。空间上以高斯核分布的外力应用于物体上随机选取的点。测试在相同的刚性形状的实例上执行，但新的力矢量和作用点会导致新的轨迹。结果可以在补充图F.9c-d中看到，说明HRN正确地预测了切线加速物体的抛物运动轨迹、力矩引起的旋转、对初始外部脉冲的响应，以及最终物体与地板的弹性碰撞。
图5: 预测实例和真实位置 a)从平面上反弹的圆锥。b)兔子的抛物线运动。在第一坐标系上施加一个力。c)一个立方体落在斜坡上。d)圆锥与五棱柱碰撞。无重力。e)三个物体在平面上碰撞。f)积木塔倒塌。g)一块布掉在地板上并折叠起来。h)一滴液滴在地上飞溅。我们强烈建议大家观看补充材料中的视频。

**复杂的形状和表面。**在更复杂的场景中，我们训练简单的形状与平面碰撞，然后推广到复杂的非凸形状(例如兔子、鸭子、泰迪)。图5b显示了兔子的示例预测；更多例子见附图F.9g-h。

我们也检查球体和立方体落在5个复杂的表面：斜坡，楼梯，半管，碗，和一个“随机的”颠簸表面。结果见图5c和补充图F.10c-e。我们训练球体和立方体落在5个表面上，并测试新的轨迹。

**动态碰撞。**两个运动物体之间的碰撞比静态碰撞(例如物体与地面之间的碰撞)更难以预测。我们首先在零重力环境中评估这个设置，以获得纯动态碰撞。在第一次实验中，从10个形状中采样9对形状进行碰撞训练。图5d显示了对碰撞的预测，包括在训练中没有看到的形状，锥体和五棱柱，演示HRN对各种形状进行概括的能力。在补充材料中可以找到更多的例子图F.9e-f，显示训练后图形的结果。

**多对象交互。**复杂的场景包括静态表面支持的多个移动对象之间的同步交互。例如，当三个物体在一个平面上碰撞时，模型需要解决直接的物体碰撞，通过中间物体的间接碰撞，以及表面施加的力来支撑物体。为了说明HRN处理此类场景的能力，我们训练两个和三个物体(立方体、棍子、球体、椭球体、三棱柱、长方体、环面、金字塔)在平面上同时碰撞的组合。结果见图5e及附图F.10f。

我们还表明，HRN训练在二和三个物体碰撞数据推广到复杂的新场景。泛化测试是在一个倒塌的塔，一个倒塌的多米诺骨牌链和一个包含多个球体的碗上进行的。所有设置由5个对象组成。见图5f及补充图图F.9b和F.10b,g为结果。虽然预测在细节上有时与地面真实情况不同，但对人类观察者来说，结果似乎还是可信的。

**柔体。**我们用不同刚度的柔体重复同样的实验，表明HRN能正确处理运动学、外力和复杂形状和涉及柔软物体表面的碰撞。一个说明性的结果如图1所示，显示了一个非刚性立方体在变形时从地板上反弹。附加图F.9g-h显示了其他示例。

**布。**我们还试验了各种布的设置。在第一个实验中，一块布从一定高度掉到地板上，然后折叠或变形。在另一个实验中，一块布固定在两点上并来回摆动。布料的预测是非常具有挑战性的，因为布料不能弹回原来的形状，而且除了与地面的碰撞之外，还要解决自碰撞问题。为了解决这个问题，我们在碰撞模块中添加了自碰撞，即同一对象内粒子之间的碰撞关系。结果如图5g和补充图F.11所示，可以看出对布料运动变形的预测是准确的。

**液体。**为了测试我们的模型预测流体的能力，我们进行了一个简单的实验，在这个实验中，流体从一定的高度落在地板上。由于流体内的效果大多是局部的，具有小分组的平面层次结构在流体预测中效果更好。结果如图5h所示，在这个场景中训练成功预测了液滴的下落。

**对参数变化的响应。**为了评估HRN对质量、重力和刚度变化的响应，我们对这些特性变化的数据集进行训练。在测试期间，我们为相同的初始起始状态改变这些参数，并评估轨迹如何变化。在补充图F.14, F.13和F.12我们展示了每种变化的结果，举例说明物体如何在一个更强的引力场中加速得更快。

**非均匀材料。**我们利用层次化粒子图表示法来构造包含刚柔两部分的对象。在训练了具有不同形状和刚度的物体落在平面上的模型后，我们手动调整个体的刚度关系来创建半刚半软的物体并生成HRN预测。补充图F.10h显示了一个半硬半软的金字塔。请注意，对于这个例子，没有任何事实依据，因为我们超越了使用的物理模拟器的能力，它无法模拟具有异质材料的对象。

5.2 定量评估和简化模型

我们将HRN与多个基准模型和简化模型进行比较。第一个基准模型是一个简单的多层感知器(MLP)，它接受完整的粒子表示并直接输出下一个粒子状态。第二个基准模型是Battaglia等人[4]定义的交互网络。表示为全连通图，因为它对应于在全连通图上去掉我们的层次结构之后来进行计算。此外，为了显示${\varphi }_C$、${\varphi }_F$和${\varphi }_H$模块的重要性，我们将它们删除并替换为简单的替代模块。${\varphi }_F$被取代为受力模块，直接连接粒子状态并传给$\eta$。类似地，${\varphi }_C$是通过添加碰撞关系到对象关系中并直接传给$\eta$。在没有${\varphi }_H$的情况下，${\varphi }_H$被简单地删除，不被任何东西取代。接下来，我们通过与1时间步长模型进行比较展示了两个输入时间步长(t, t-1)改善了结果。最后，我们评估了保形损失和整体损失添加进局部损失的重要性。所有的模型都是针对两个立方体在平面上碰撞并被推向对方后反复碰撞的场景进行训练的。在同样的情况下，对模型进行了无重力轨迹测试。对不同分组方法的补充评价见补充材料B节。

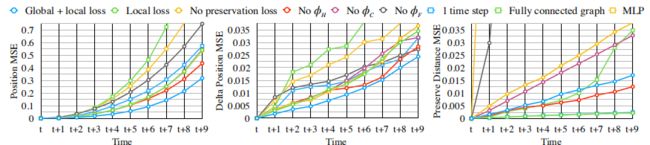图6:定量评估。我们将全HRN(全局+局部损失)与几个基准模型和简化模型进行比较，即只有局部损失、没有保存损失、没有${\varphi }_H$、没有${\varphi }_C$、没有${\varphi }_F$”、1时间步长、全连通图和MLP基准模型。从左到右的线图显示了随着时间积累的位置、位移和距离保持之间的平均平方误差(MSE)。我们的模型具有最小的位置和增量的位置误差和仅略高的保形误差。

比较指标是时间步长t + 9前的绝对全局位置的累积平均平方误差、局部位移和保形误差。结果如图6所示。HRN在大多数情况下优于所有控件。由于全连通图和MLP基准模型的性能显著下降，因此层次结构尤其重要。另外，不采用层次化图卷积机制的HRN的性能明显差，如图C.4所示，说明了连续三个图卷积阶段的必要性。在定性评估中，我们发现使用一个以上的输入时间步长可以改善结果，特别是在碰撞过程中，因为加速度得到了更好的估计，图6中的指标证实了这一点。我们还发现，将碰撞、力、历史和影响传播分解成具有独立权重的独立模块，可以使每个模块专门化，改进预测。最后，提出的损失结构对模型训练至关重要。如果没有保形或全局位移预测，我们的模型的性能会差很多。关于损耗和图结构的进一步讨论，请参阅补充材料C。

5.3 讨论

我们的结果表明，绝大多数复杂的多目标相互作用都能很好地预测，包括非凸几何图形之间的多点碰撞，以及像碗中包含多个滚动球这样的复杂场景。虽然没有展示，在理论上，人们也可以通过消除物体内部粒子之间的足够多的关系来模拟物体粉碎。这些操作非常有趣，因为它们超出了在我们的模拟环境中可能生成的内容。此外，对特别具有挑战性的情况的预测，比如多块塔的预测，也是最有效的，当塔倒塌时，物体(大部分)保持它们的形状，互相翻滚(见补充材料和视频)。随着时间的推移，形状保存的损失可以部分归因于递归滚出所产生的复合错误。尽管如此，我们的模型预测塔倒塌的速度比地面情况要快。当物体应该绝对静止时，预测也会抖动。这些失败主要是由于训练集只包含快速移动的对象对或三联对象之间的交互，而没有对象处于静止状态的场景。它推广到塔以及它所做的是我们的方法的一个强有力的说明。对静止的对象添加一小部分训练观察，可以使塔的行为更加真实，并消除总体上的抖动。训练数据对最终模型的性能和泛化能力起着至关重要的作用。理想情况下，训练集将涵盖世界上所有的物理现象。然而，手工设计这样的数据集是非常棘手的，几乎是不可能的。因此，自我驱动的agent建立自己的物理实验的方法对于最大限度地学习和理解将是至关重要的[19]。

6 结论

我们描述了一个基于图的层次化场景表示，它允许任意规格的任何几何形状和各种材质属性。利用这种表示法，我们引入了一种基于层次化图卷积的可学习神经网络，它可以在较长时间范围内为复杂的物理相互作用生成可行的轨迹，并在形状、质量、内外力和材料属性等方面进行推广。由于我们的表示本质上是以粒子为基础，它本质上表现了认知科学中的客体永久性这个人类对象感知的关键特征[43]。

这项工作的广泛应用是可能的。其中包括开发机器人技术中抓取刚性和柔性物体的预测模型，以及为视频游戏或其他仿真建模3D点云扫描的物理模型。为了使基于像素的端到端可训练版本的HRN能够用于关键的计算机视觉应用，将我们的工作与现有方法(例如[54,23,15])的调整结合起来，从LIDAR/RGBD/RGB图像或视频数据推导初始(非层次化)场景图将是至关重要的。在未来，我们还计划弥补HRN的一些局限，扩展它可以处理的材料类别，包括可充气的物体或者气体，以及对象可以拆开或合并的动态场景。这应该包括更复杂的材料属性表示以及更微妙的层次结构。最后，评估HRN类型的模型在多大程度上描述了认知科学家观察到的人类直觉物理知识的模式将是非常有趣的[32,35,38]。