手把手教你使用R语言做竞争风险模型并绘制列线图
竞争风险模型就是指在临床事件中出现和它竞争的结局事件,这是事件会导致原有结局的改变,因此叫做竞争风险模型。比如我们想观察患者肿瘤的复发情况,但是患者在观察期突然车祸死亡,或者因其他疾病死亡,这样我们就观察不到复发情况了,这种情况下不能把缺失数据仅仅当做右删失处理,这样的话会造成数据的估值错误。这是我们应该优先选择竞争风险模型来做数据分析,而不是COX回归。竞争风险模型在数据挖掘中经常使用到,我们将来在SEER数据库挖掘教程中将介绍怎么使用竞争风险模型进行数据挖掘。
我们使用R语言survival自带的膀胱癌bladder1的数据集,为了使它符合竞争风险模型的要求,我们做了一点小小的整理,我们要观察的是肿瘤复发,因此死亡就是它的风险竞争因素。
首先我们把需要的R导入,然后导入数据
library(foreign)
library(survival)
library("cmprsk")
library(rms)
be<-read.csv("E:/r/test/jzfx.csv",sep=',',header=TRUE)
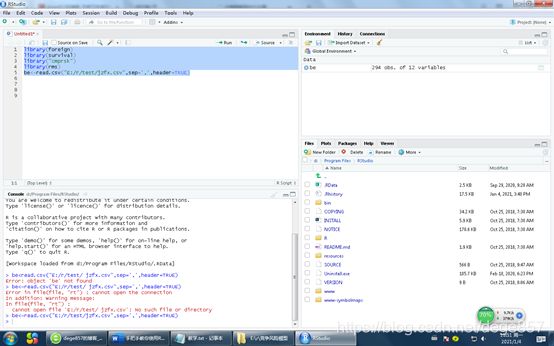
我们来看一下数据是什么样子的

数据的名称解释为:
id: 患者编号;treatment(治疗方案):1. 安慰剂2. 维生素B6. 3.噻替帕 ;
number: 肿瘤的初始数量 size: 最大的初始肿瘤大小(厘米) recur: 复发次数
start,stop: 开始,停止:每个时间间隔的开始和结束时间 status(结局):1.存活2.复发3.死亡 rtumor: 复发时发现的肿瘤数量 rsize: 复发时最大的肿瘤大小
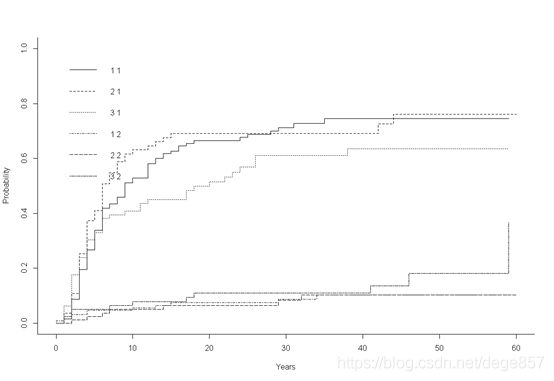
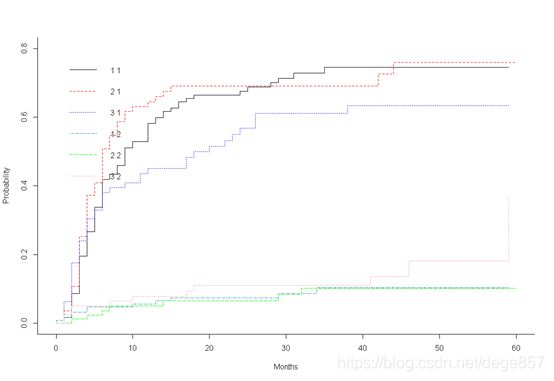
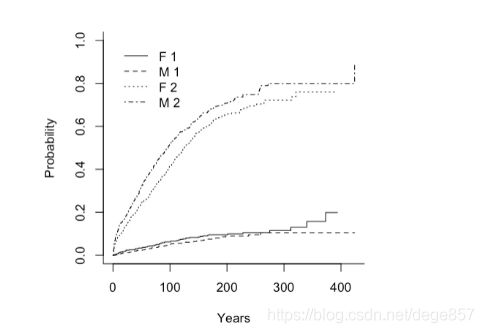
## 不同治疗方案的复发率和竞争事件发生率
cum<-cuminc(be$etime,be$status,be$treatment)
plot(cum)
## 多因素竞争风险模型-复发的发生率(或竞争事件的发生率,failcode = 2)
time<-be$etime
status<-be$status
x <- be[, c('treatment', 'number', 'size','recur')]
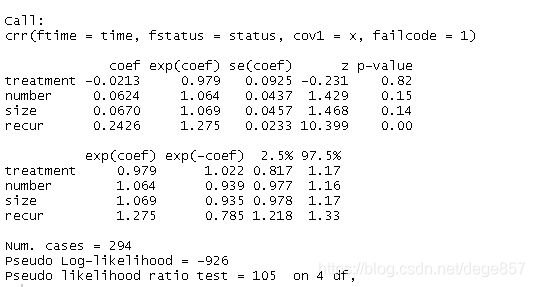
fit2 <- crr(time,status,x,failcode = 1)#这里failcode = 1代表肿瘤复发
summary(fit2)
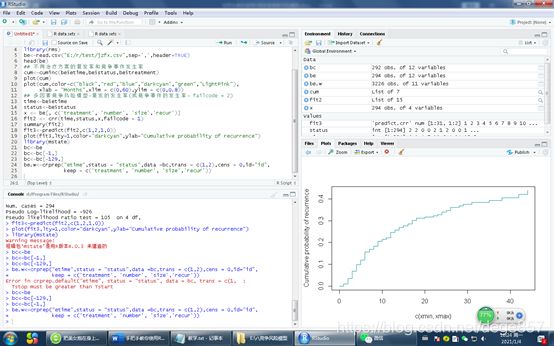
fit3<-predict(fit2,c(1,2,1,0)) #对应数据X的4个指标
plot(fit3,lty=1,color="darkcyan",ylab="Cumulative probability of recurrence")
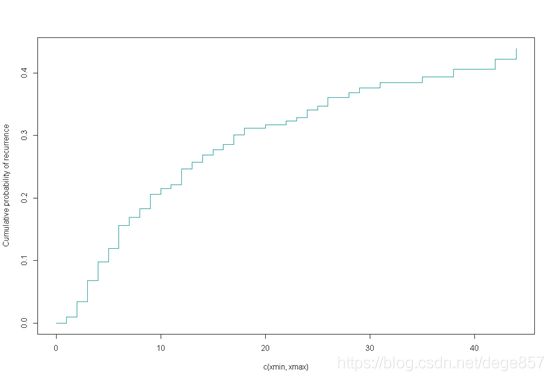
##下面我们来做列线图
首先要对数据进行加权,为什么要加权呢,原理很复杂,涉及到竞争风险模型的原理,我也不知道,但是大牛们都说要加权我们就加吧。
library(mstate)
bc<-be
bc<-bc[-1,]
bc<-bc[-129,]
be.w<-crprep("etime",status = "status",data =bc,trans = c(1,2),cens = 0,id="id",
keep = c('treatment', 'number', 'size','recur'))#进行加权
be.w$Time<-be.w$Tstop-be.w$Tstart#添加个时间,好进行COX回归
dd<-datadist(be.w)
options(datadist="dd")
f <- cph(Surv(Tstart,Tstop,status==1) ~ treatment+number+size+recur, x=T, y=T,
surv=T, data=be.w, time.inc=36)#建立COX回归
surv<- Survival(f)#生成预测函数
nom <- nomogram(f, fun=list(function(x) surv(36, x),
function(x) surv(60, x)),
funlabel=c("3-year survival Probability",
"5-year survival Probability"))#制作列线图
plot(nom)
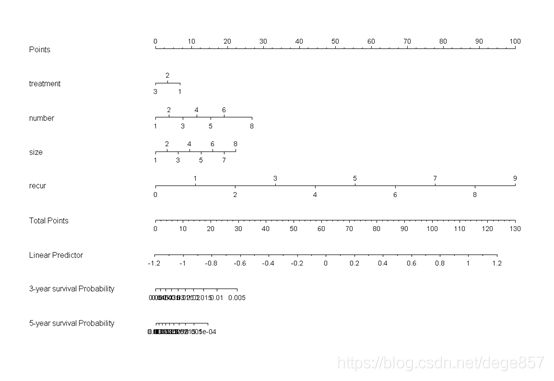
这个列线图有点丑,主要是这个概率太小了,有兴趣的可以自己调整一下
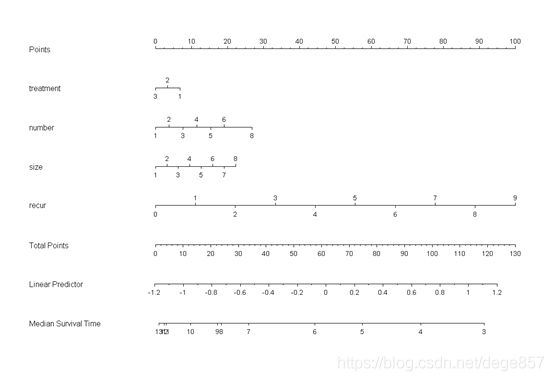
###中位数列线图
med <- Quantile(f) # 计算中位生存时间
nom2 <- nomogram(f, fun=function(x) med(lp=x),funlabel="Median Survival Time")
plot(nom2)