机器学习的基本概念

监督与无监督的概念

机器学习主要包括监督学习、无监督学习和强化学习。

由于我们的课程是面向机器学习入门的同学，所以我主要介绍监督和无监督学习的部分，强化学习的部分不做介绍。

首先，什么是监督学习呢？它和无监督学习的区别又是什么呢？

监督学习是指从标注数据中学习预测模型的机器学习问题。相反的，无监督学习是指从无标注数据中学习预测模型的机器学习问题。

由此可知：监督学习和无监督学习的区别在于数据是否有标注，那么数据一般长什么样呢？标注指的又是什么呢？

样本、特征、标记

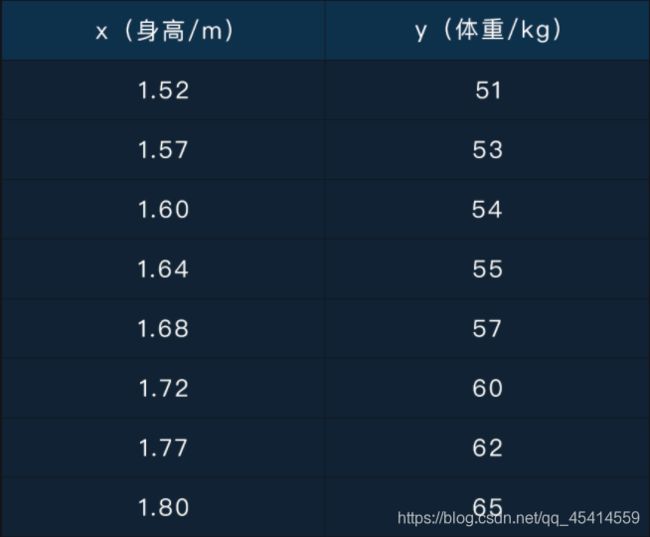
为了让你对数据有一个直观的印象，我们先来看一张表格：

这其实是上节课讲到的那个利用身高预测体重的数据，表格中的每一行都代表着一条样本数据；表格的第一列 x 在机器学习中的术语叫做特征（feature），第二列 y 在机器学习中的术语叫做标记（label），也就是刚才提到的标注。

你是否还记得第 1 节课的最后一个习题：我们需要同时具备大量的身高和体重数据才能学习到模型 y = kx+b 。其中的 x （身高）是输入特征， y（体重）是输出标记。这就属于一个监督学习的问题，假如没有标记值 y ，是无法学习到模型参数 k 和 b 的。

分类与回归

根据预测 y 值类型的不同，监督学习主要有两个方面的应用：分类问题和回归问题。

分类问题中预测的 y 值是离散值，一般取值的个数是有限的，比如性别、职业、省份等；回归问题中预测的 y 值是连续值，一般取值的个数是无限的，比如身高、体重、收入等。

不仅 label 有连续和离散之分，特征 x 按照取值个数是否有限也会有连续型特征和离散型特征的区别。

问：有一种说法是：类别型变量都是离散值，数值型变量都是连续值，你觉得对吗？
A：对 B：不对
答案：B 连续和离散的判定标准是取值是否有限，取值有限的是离散型变量，取值无限的是连续型变量。类别型变量的取值一般都是有限的，例如省份的取值，所以类别型变量都是离散值。而数值型变量的取值可以是有限的也可以是无限的。

比如我用一个变量 x 来表示 “一个人的年龄区间”，取值为0时代表"18岁以下"，取值为1时代表"18-30岁"，取值为2代表“30-50岁”，取值为3代表"50岁以上"，这种情况下数值型变量 x 的取值只有4个，它属于离散值。前面例子中的身高值 x 属于连续值，因为身高从1米到2米之间，你可以取任意值，数量是无限的。

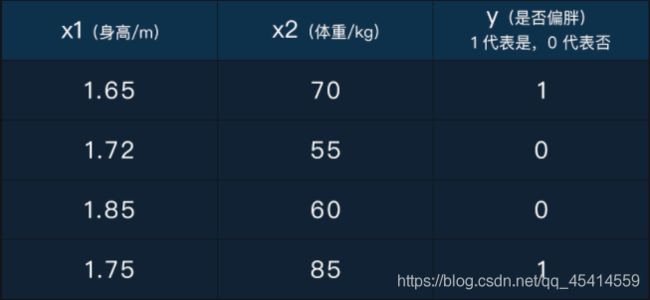
利用身高预测体重的例子其实是一个典型的回归问题，下面我们再来看一张分类问题中的数据表：

这张表中x1和x2都是样本的特征，且都是连续型特征；y是样本的标记，取值为0或1，所以 y 属于离散型数值变量，也可以叫类别型变量：取值0和1分别代表了两个人群的类别。

对比回归问题中的数据表：除了y值类型的不同，这张数据表的特征是不止一个的。事实上，不管是分类还是回归，模型的输入特征都可以是多维的，体现在这张表中是两维特征。

问：假如你现在有大量抖音用户的视频点击数据，要求你根据这些数据训练一个模型，去预测用户下次观看某个视频时是否会给这个视频点赞。这个问题属于监督学习中的（）
A： 分类问题 B：回归问题
答案：A 预测用户是否点赞，在机器学习中对应预测的 y 值是个离散值，取值为 “是” 或 “否” ，所以属于分类问题。

训练集与测试集

当我们有了数据之后，该如何去使用数据训练模型呢？是把上面那样的数据全部丢给模型进行训练吗？

仔细想一下，这样做是不合理的。因为我们需要知道训练好的模型在未知数据上的预测效果到底怎么样，所以就需要拿出一部分不参加训练的数据用于测试模型的预测效果。

我们需要把整个数据集切分成训练集和测试集两部分，训练集用于模型的训练，测试集用于模型的测试。例如，我们有1000行数据，就可以取800行数据作为训练集，剩下的200行作为测试集。

数据拟合与模型泛化

可能你又会问，直接在训练数据上测试模型的预测效果不可以吗？

答案是不可以，因为在模型训练的过程中，模型的预测输出值是不断地拟合与逼近真实的 y 值的，这是模型训练的目标和使命。

我们训练模型的目的并不是为了预测已知的训练数据，而是要预测未知数据，让模型在未知数据上取得良好的预测效果。

模型在未知数据上的预测效果越好，说明它的泛化能力越强。但如果一味地拟合训练数据，就会导致模型过拟合 。

过拟合最明显的表现就是模型在训练数据上的预测效果很好，但是在测试数据上的预测效果很差，这其实也是模型泛化能力差的表现。

过拟合与相应的解决办法是面试中常考的问题，关于这部分内容的理解我会在后面的章节中专门用一节课去讲解。

过拟合的反面是欠拟合，也就是模型对训练数据的拟合程度不够，导致在训练数据上的误差较大，这种情况下模型在测试数据上的表现一般也不好。

下面我们看一下回归问题中对于数据拟合的直观解释：

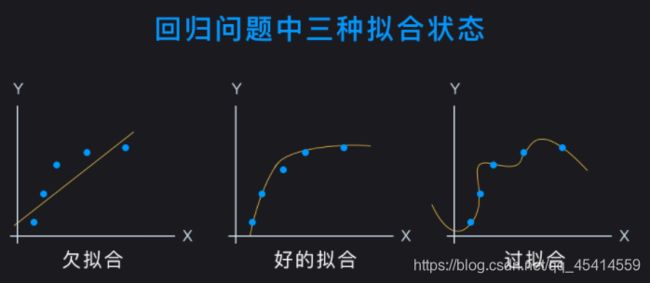
图中的横轴是特征 x ，纵轴是标记 y 。蓝色数据点是训练数据，黄色曲线是学习到的模型曲线，也就是函数 y = f(x) 。

欠拟合时，模型没有学习到数据的一般规律，曲线较简单；过拟合则是拟合每一个数据点，模型曲线较为复杂。好的拟合曲线是可以反映大部分数据点的规律，有一定的泛化能力。

下面再来看一下分类问题中对于数据拟合的直观解释：

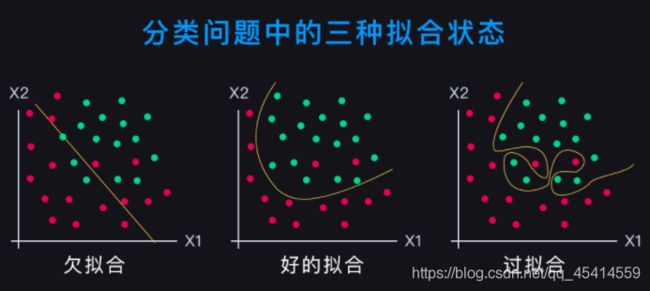
图中的横轴和纵轴都是特征，数据的标记值 y 体现在数据点的颜色上，不同的颜色代表不同的 y 值。黄色曲线是分类模型的分类边界线。

欠拟合的情况下，分类边界线比较简单，两侧有较多的误分类点；过拟合的情况下，分类边界线比较曲折，两侧几乎没有误分类点。

好的分类边界线是一条光滑的边界线，它可以把大部分数据点正确分类，反映了数据整体的分布规律。

问：当一个模型出现了明显的过拟合现象，那么它的泛化能力高还是低？
A：高 B：低
答案：B 过拟合指的是训练误差较小而测试误差却很大的现象，对应的模型泛化能力较差。就好比你准备一次考试，考前练习了大量的习题，但你只是机械地记忆，不懂得举一反三，考试遇到类似的问题还是不会做。这里的 “举一反三” 和泛化能力表达的是一个意思。

聚类和降维

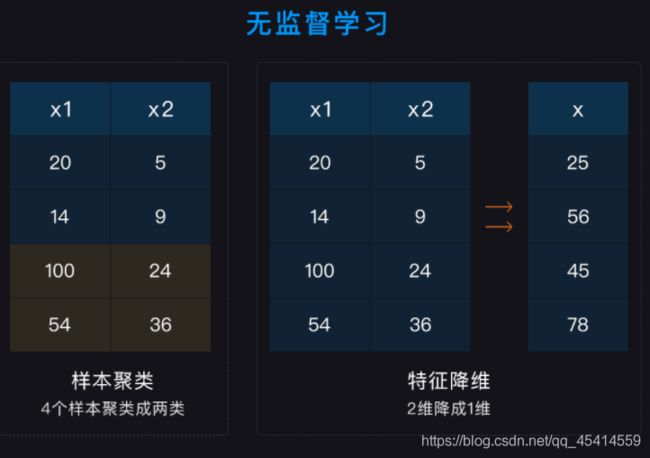
无监督学习的应用主要有两个方面：样本聚类和特征降维。在数据上的表现形式如下：

从上面这张图可以看到：样本聚类是数据纵向的压缩；而特征降维是数据横向的压缩。

问：如图所示，假如你有一张虚拟的个人信息表（大概500条数据），要求你根据这些数据将所有的样本分成 5 类。这个问题属于机器学习中的（）

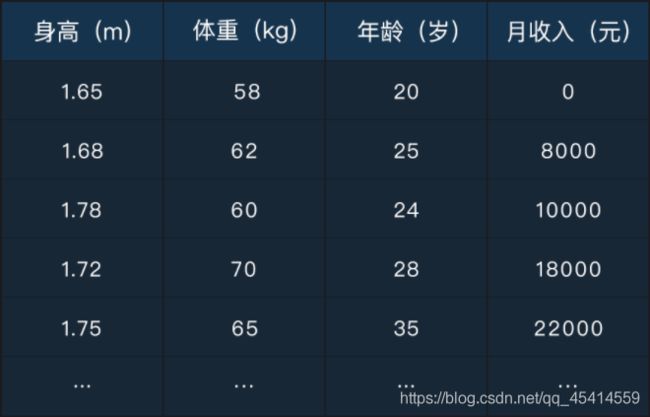
A：分类问题 B：聚类问题
答案：B 分类问题和聚类问题的本质区别在于：分类属于监督学习的范畴，而聚类属于无监督学习的范畴；所以这道题判断分类和聚类的关键是所给的数据集是否有标注信息（即预测的 y 值）。很显然，身高、体重、年龄、月收入都属于样本的特征 。

模型参数与超参数

模型参数是可学习的，比如一次线性函数的斜率和截距。

模型的超参数是人为设定的，比如迭代次数，即：模型在整个训练集上重复训练的次数。