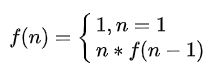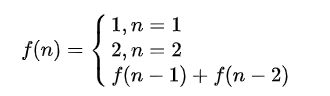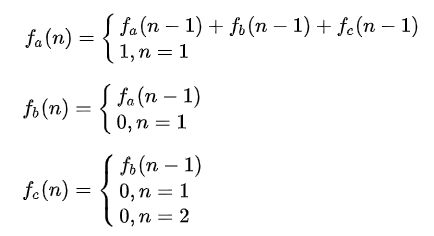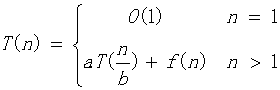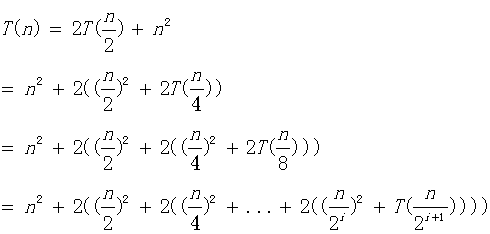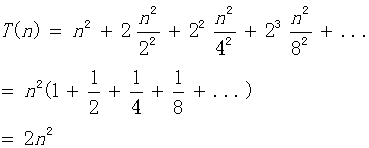导论
小编之前在分享有关的算法时,把递归这一重要的算法设计思想给遗漏了。递归的学习绝对是一个持久战,没有人可以一蹴而就。问题的复杂,加上递归本身的细节,我们想要“学会”、“学好”再到“用好”,是需要一个漫长的过程的。说实话,哪来那么多捷径啊!小编整理了下一些写的比较好的文章,希望对各位小伙伴有所帮助。
本文试图从以下几个方面来讲解递归
1、什么是递归?
2、递归算法通用解决思路
3、实战演练(从初级到高阶)
4、递归函数调用栈
5、递归算法时间复杂度分析与求解
力争让大家对递归的认知能上一个新台阶,特别会对递归的精华:时间复杂度作详细剖析,会给大家总结一套很通用的求解递归时间复杂度的套路,相信你看完肯定会有收获。
什么是递归
简单地说,就是如果在函数中存在着调用函数本身的情况,这种现象就叫递归。
以阶乘函数为例,如下, 在 f 函数中存在着 f(n - 1) 的调用,所以此函数是递归函数。
\\求阶乘函数
int f(int n) {
if (n < =1) {
return 1;
}
return n * f(n - 1)
}
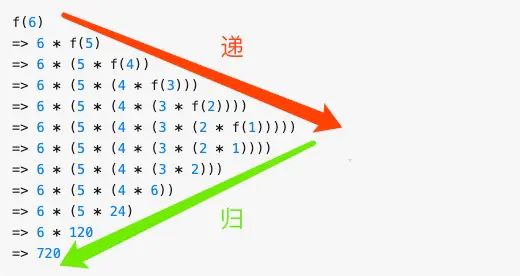
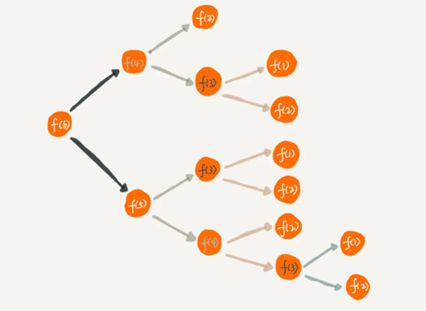
进一步剖析「递归」,先有「递」再有「归」,「递」的意思是将问题拆解成子问题来解决, 子问题再拆解成子子问题,...,直到被拆解的子问题无需再拆分成更细的子问题(即可以求解),「归」是说最小的子问题解决了,那么它的上一层子问题也就解决了,上一层的子问题解决了,上上层子问题自然也就解决了,....,直到最开始的问题解决,文字说可能有点抽象,那我们就以阶层 f(6) 为例来看下它的「递」和「归」。
求解问题 f(6), 由于 f(6) = n * f(5), 所以 f(6) 需要拆解成 f(5) 子问题进行求解,同理 f(5) = n * f(4) ,也需要进一步拆分,... ,直到 f(1), 这是 「递」,f(1) 解决了,由于 f(2) = 2 f(1) = 2 也解决了,.... f(n)到最后也解决了,这是 「归」,所以递归的本质是能把问题拆分成具有相同解决思路的子问题,。。。直到最后被拆解的子问题再也不能拆分,解决了最小粒度可求解的子问题后,在「归」的过程中自然顺其自然地解决了最开始的问题。
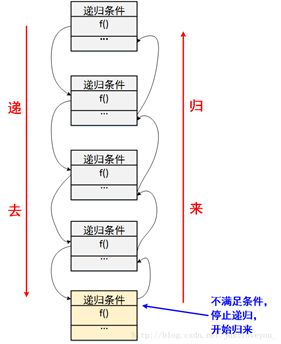
这里放一幅图,主要来表示递归的终止是有条件的,在求阶乘这个问题里,递归的终止条件就是n<1。
递归算法通用解决思路
我们在上一节仔细剖析了什么是递归,可以发现递归有以下两个特点:
1、一个问题可以分解成具有相同解决思路的子问题,子子问题,换句话说这些问题都能调用同一个函数
2、经过层层分解的子问题最后一定是有一个不能再分解的固定值的(即终止条件),如果没有的话,就无穷无尽地分解子问题了,问题显然是无解的。
所以解递归题的关键在于我们首先需要根据以上递归的两个特点判断题目是否可以用递归来解。
经过判断可以用递归后,接下来我们就来看看用递归解题的基本套路(四步曲):
1、先定义一个函数,明确这个函数的功能,由于递归的特点是问题和子问题都会调用函数自身,所以这个函数的功能一旦确定了, 之后只要找寻问题与子问题的递归关系即可
2、接下来寻找问题与子问题间的关系(即递推公式),这样由于问题与子问题具有相同解决思路,只要子问题调用步骤 1 定义好的函数,问题即可解决。所谓的关系最好能用一个公式表示出来,比如 f(n) = n * f(n-) 这样,如果暂时无法得出明确的公式,用伪代码表示也是可以的, 发现递推关系后,要寻找最终不可再分解的子问题的解,即(临界条件),确保子问题不会无限分解下去。由于第一步我们已经定义了这个函数的功能,所以当问题拆分成子问题时,子问题可以调用步骤 1 定义的函数,符合递归的条件(函数里调用自身)
3、 将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中
4、最后也是很关键的一步,根据问题与子问题的关系,推导出时间复杂度,如果发现递归时间复杂度不可接受,则需转换思路对其进行改造,看下是否有更靠谱的解法。
听起来是不是很简单,接下来我们就由浅入深地来看几道递归题,看下怎么用上面的几个步骤来套。
实战演练(从初级到高阶)
热身赛
输入一个正整数n,输出n!的值,即求阶乘
套用上一节我们说的递归四步解题套路来看看怎么解
1、定义这个函数,明确这个函数的功能,我们知道这个函数的功能是求 n 的阶乘, 之后求 n-1, n-2 的阶乘就可以调用此函数了。
\\求阶乘函数
int f(int n) {
}
2、寻找问题与子问题的关系 阶乘的关系比较简单, 我们以 f(n) 来表示 n 的阶乘, 显然 f(n) = n * f(n - 1), 同时临界条件是 f(1) = 1,即:
3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中。
\\求阶乘函数
int f(int n) {
if (n < =1) {
return 1;
}
return n * f(n - 1)
}
4、求时间复杂度 由于 f(n) = n * f(n-1) = n * (n-1) * .... * f(1),总共作了 n 次乘法,所以时间复杂度为 n。
看起来是不是有这么点眉目, 当然这道题确实太过简单,很容易套路,那我们再来看进阶一点的题。
入门题
一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶,例如:跳上第 1 级台阶只有一种跳法:直接跳 1 级即可。 跳上第 2 级台阶有两种跳法:每次跳 1 级,跳两次;或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法?
我们继续来按四步曲来看怎么套路
1、定义一个函数,这个函数代表了跳上 n 级台阶的跳法
/**
* 跳 n 极台阶的跳法
*/
int f(int n) {
}
2、寻找问题与子问题之前的关系:
这两者之前的关系初看确实看不出什么头绪,但仔细看题目,一只青蛙只能跳一步或两步台阶,自上而下地思考,也就是说如果要跳到 n 级台阶只能从 从 n-1 或 n-2 级跳, 所以问题就转化为跳上 n-1 和 n-2 级台阶的跳法了,如果 f(n) 代表跳到 n 级台阶的跳法,那么从以上分析可得 f(n) = f(n-1) + f(n-2),显然这就是我们要找的问题与子问题的关系,而显然当 n = 1, n = 2, 即跳一二级台阶是问题的最终解,于是递推公式系为:
3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中 补充后的函数如下:
/**
* 跳 n 极台阶的跳法
*/
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2)
}
4、计算时间复杂度:
斐波那契的时间复杂度计算涉及到高等代数的知识, 这里不做详细推导,有兴趣的同学可以点击小编以前的文章查看,我们直接结出结论:
由些可知时间复杂度是指数级别,显然不可接受,那回过头来看为啥时间复杂度这么高呢,假设我们要计算 f(6),根据以上推导的递归公式,展示如下:
可以看到有大量的重复计算, f(3) 计算了 3 次, 随着 n 的增大,f(n) 的时间度自然呈指数上升了。
5、优化算法1 :
既然有这么多的重复计算,我们可以想到把这些中间计算过的结果保存起来,如果之后的计算中碰到同样需要计算的中间态,直接在这个保存的结果里查询即可,这就是典型的以空间换时间,改造后的代码如下:
int helper(vector& result,int n){
if(n==1)return 1;
if(n==2)return 2;
if(result[n]!=0)return result[n];
result[n]=helper(result,n-1)+helper(result,n-2);
return result[n];
}
int f(int N){
if(N<1) return 0;
vector result(N+1,0);
return helper(result,N);
}
"记忆化搜索"或者我们称"重叠子问题"的加缓存优化的实现,我们的思考路径是"自顶向下"。即为了解决数据规模大的问题,我们“假设”已经解决了数据规模较小的子问题。我们没有从最基本的问题开始求解,对于f(n)=f(n-1)+f(n-2),我们假装f(n-1)和f(n-2)是已知的。那么改造后的时间复杂度是多少呢,由于对每一个计算过的 f(n) 我们都保存了中间态 ,不存在重复计算的问题,所以时间复杂度是 O(n), 但由于我们用了一个键值对来保存中间的计算结果,所以空间复杂度是 O(n)。
6、优化算法2:
我们可以使用动态规划的思想来编写程序,同样,其时间复杂度与空间复杂度都为O(n)。代码如下:
int f(int N){
if(N<1) return 0;
vector result(N+1,0);
result[1]=1;
result[2]=2;
for(int i=3;i<=N;i++){
result[i]=result[i-1]+result[i-2];
}
return result[N];
}
7、优化算法3:
问题到这里其实已经算解决了,但身为有追求的程序员,我们还是要问一句,空间复杂度能否继续优化?这里直接给出代码,如下所示:
int f(int N){
if(N==1)return 1;
if(N==2)return 2;
int result=0;
int pre=1;
int next=2;
for(int i=3;i<=N;i++){
result=pre+next;
pre=next;
next=result;
}
return result;
}
简单总结一下: 分析问题我们需要采用自上而下的思维,而解决问题有时候采用自下而上的方式能让算法性能得到极大提升,思路比结论重要。
初级题
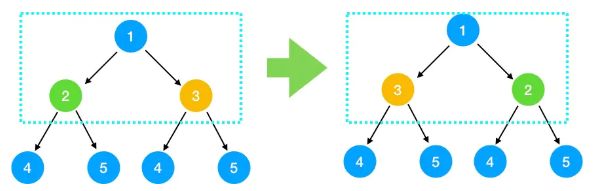
接下来我们来看下一道经典的题目: 反转二叉树:将左边的二叉树反转成右边的二叉树。
接下来让我们看看用我们之前总结的递归解法四步曲如何解题:
1、定义一个函数,这个函数代表了 翻转以 root 为根节点的二叉树
struct BinaryTreeNode{
char val;
BinaryTreeNode *lchild;
BinaryTreeNode *rchild;
};
typedef BinaryTreeNode *BinaryTree;
BinaryTree InvertBinaryTree(BinaryTree &root){
}
2、查找问题与子问题的关系,得出递推公式 我们之前说了,解题要采用自上而下的思考方式,那我们取前面的1, 2,3 结点来看,对于根节点 1 来说,假设 2, 3 结点下的节点都已经翻转,那么只要翻转 2, 3 节点即满足需求。
对于2, 3 结点来说,也是翻转其左右节点即可,依此类推,对每一个根节点,依次翻转其左右节点,所以我们可知问题与子问题的关系是: 翻转(根节点) = 翻转(根节点的左节点) + 翻转(根节点的右节点),即:
InvertBinaryTree(root) = InvertBinaryTree(root->lchild) + InvertBinaryTree(root->rchild)
而显然递归的终止条件是当结点为叶子结点时终止(因为叶子节点没有左右结点)
3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中。
BinaryTree InvertBinaryTree(BinaryTree &root){
if(root=NULL) return NULL;
root->lchild=InInvertBinaryTree(root->lchild);
root->rchild=InInvertBinaryTree(root->rchild);
BinaryTree tempTree=root->lchild;
root->lchild=root->rchild;
root->rchild=tempTree;
return root;
}
4、时间复杂度分析
由于我们会对每一个节点都去做翻转,所以时间复杂度是 O(n),那么空间复杂度呢,这道题的空间复杂度非常有意思,我们一起来看下,由于每次调用InvertBinaryTree函数都相当于一次压栈操作, 那最多压了几次栈呢, 仔细看上面函数的下一段代码:
root->lchild=InInvertBinaryTree(root->lchild);
从根节点出发不断对左结果调用翻转函数, 直到叶子节点,每调用一次都会压栈,左节点调用完后,出栈,再对右节点压栈....,下图可知栈的大小为3, 即树的高度,如果是完全二叉树 ,则树的高度为logn, 即空间复杂度为O(logn)。
最坏情况,如果此二叉树是如图所示(只有左节点,没有右节点),则树的高度即结点的个数 n,此时空间复杂度为 O(n)。总的来看,空间复杂度为O(n)。
中级题
接下来我们看一下大学时学过的汉诺塔问题:
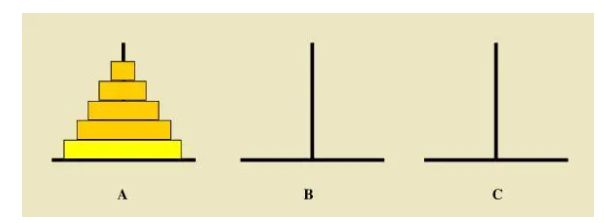
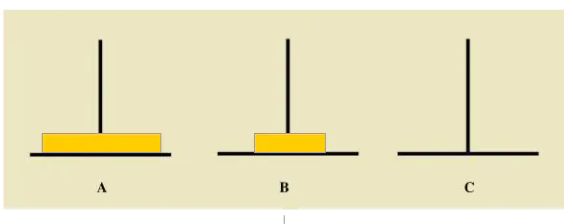
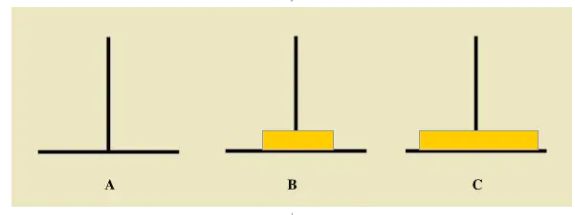
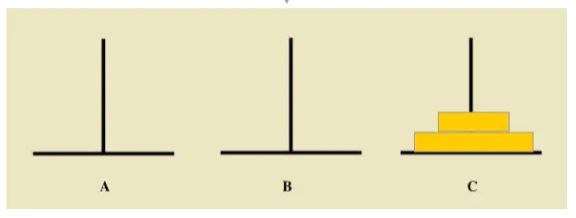
如下图所示,从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数。
接下来套用我们的递归四步法看下这题怎么解:
1、定义问题的递归函数,明确函数的功能,我们定义这个函数的功能为:把 A 上面的 n 个圆盘经由 B 移到 C
void hannoi (int n, char a, char b, char c) // 将 n 个圆盘从 A 经由 B 移动到 C 上
{
}
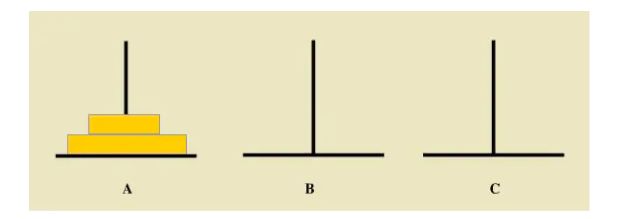
2、查找问题与子问题的关系 首先我们看如果 A 柱子上只有两块圆盘该怎么移:
前面我们多次提到,分析问题与子问题的关系要采用自上而下的分析方式,要将 n 个圆盘经由 B 移到 C 柱上去,可将 上面的 n-1 个圆盘看成是一个圆盘,这样分析思路就与上面提到的只有两块圆盘的思路一致了,分三步走:
(1)将上面的 n-1 个圆盘经由 C 移到 B
(2)此时将 A 底下的那块最大的圆盘移到 C
(3)再将 B 上的 n-1 个圆盘经由A移到 C上
有人问第一步的 n - 1 怎么从 C 移到 B,重复上面的过程,只要把 上面的 n-2个盘子经由 A 移到 B, 再把A最下面的盘子移到 C,最后再把上面的 n - 2 的盘子经由A 移到 B 下..., 怎么样,是不是找到规律了,不过在找问题的过程中 切忌把子问题层层展开,到汉诺塔这个问题上切忌再分析 n-3,n-4 怎么移,这样会把你绕晕,只要找到一层问题与子问题的关系得出可以用递归表示即可。
由以上分析可得:
move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C)
一定要先得出递归公式,哪怕是伪代码也好!这样第三步推导函数编写就容易很多,终止条件我们很容易看出,当 A 上面的圆盘没有了就不移了
3、根据以上的递归伪代码补充函数的功能:
void hanoid(int n, char a, char b, char c) {
if (n <= 0) {
return;
}
// 将上面的 n-1 个圆盘经由 C 移到 B
hanoid(n-1, a, c, b);
// 此时将 A 底下的那块最大的圆盘移到 C
move(a, c);
// 再将 B 上的 n-1 个圆盘经由A移到 C上
hanoid(n-1, b, a, c);
}
void move(char a, char b) {
printf("%c->%c\n", a, b);
}
从函数的功能上看其实比较容易理解,整个函数定义的功能就是把 A 上的 n 个圆盘 经由 B 移到 C,由于定义好了这个函数的功能,那么接下来的把 n-1 个圆盘 经由 C 移到 B 就可以很自然的调用这个函数,所以明确函数的功能非常重要,按着函数的功能来解释,递归问题其实很好解析,切忌在每一个子问题上层层展开死抠,这样这就陷入了递归的陷阱,计算机都会栈溢出,何况人脑。
4、时间复杂度分析 从第三步补充好的函数中我们可以推断出:
f(n) = f(n-1) + 1 + f(n-1)
= 2f(n-1) + 1
= 2(2f(n-2) + 1) + 1
= 2 * 2 * f(n-2) + 2 + 1
= 22 f(n-2) + 2 + 1
= 22(2f(n-3)+1) + 2 + 1
= 23 f(n-3) + 22+2 + 1
=……
= 2n-1 + 2n-2 + ....+ 1
显然时间复杂度为 O(2n),很明显指数级别的时间复杂度是不能接受的,汉诺塔非递归的解法比较复杂,大家可以去网上搜一下。
进阶题
现实中大厂中的很多递归题都不会用上面这些相对比较容易理解的题,更加地是对递归问题进行相应地变形, 来看下面这道题:
“细胞分裂 有一个细胞 每一个小时分裂一次,一次分裂一个子细胞,第三个小时后会死亡。那么n个小时候有多少细胞?”
照样我们用前面的递归四步曲来解:
1、定义问题的递归函数,明确函数的功能 我们定义以下函数为 n 个小时后的细胞数。
int allCells(int n) {
}
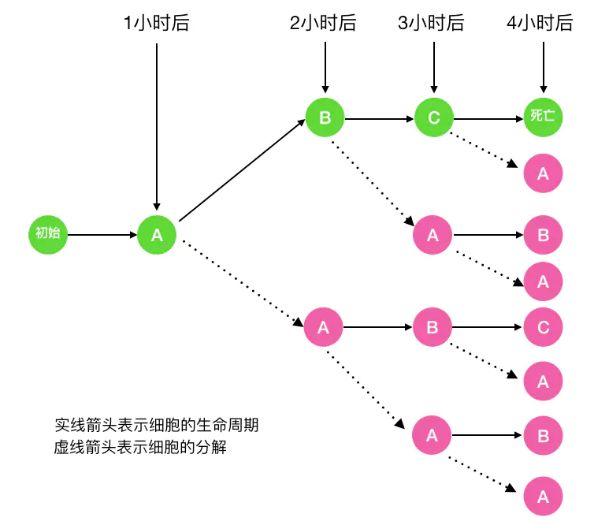
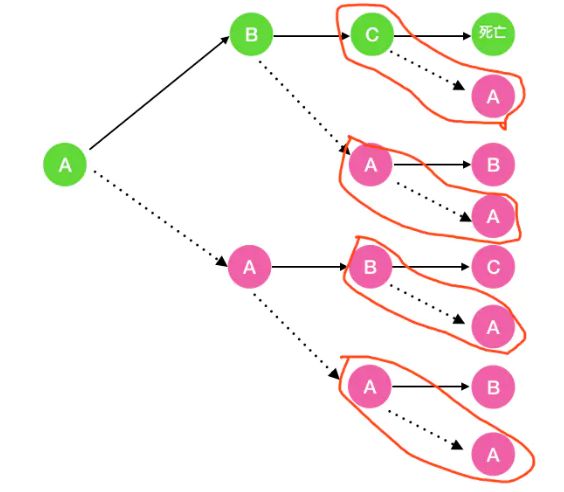
2、接下来寻找问题与子问题间的关系(即递推公式) 首先我们看一下一个细胞出生到死亡后经历的所有细胞分裂过程。
图中的 A 代表细胞的初始态, B代表幼年态(细胞分裂一次), C 代表成熟态(细胞分裂两次),C 再经历一小时后细胞死亡
以 f(n) 代表第 n 小时的细胞分解数:
fa(n) 代表第 n 小时处于初始态的细胞数,
fb(n) 代表第 n 小时处于幼年态的细胞数
fc(n) 代表第 n 小时处于成熟态的细胞数
则显然 f(n) = f a(n) + f b(n) + f c(n)
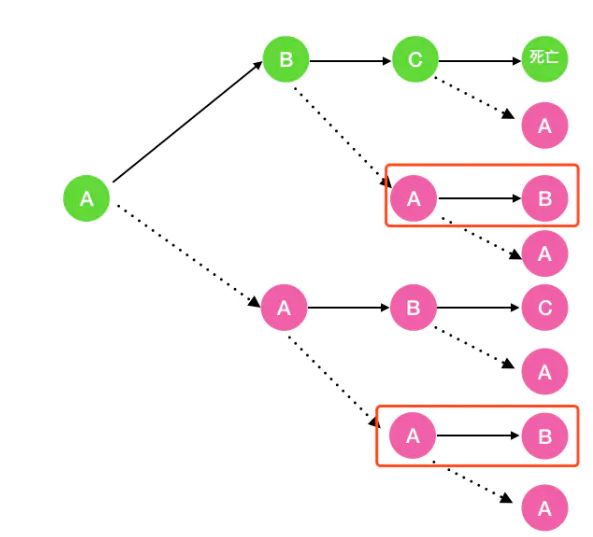
那么 f a(n) 等于多少呢,以n = 4 (即一个细胞经历完整的生命周期)为例
仔细看上面的图:
可以看出 f a(n) = f a(n-1) + f b(n-1) + f c(n-1), 当 n = 1 时,显然 f a(1) = 1。
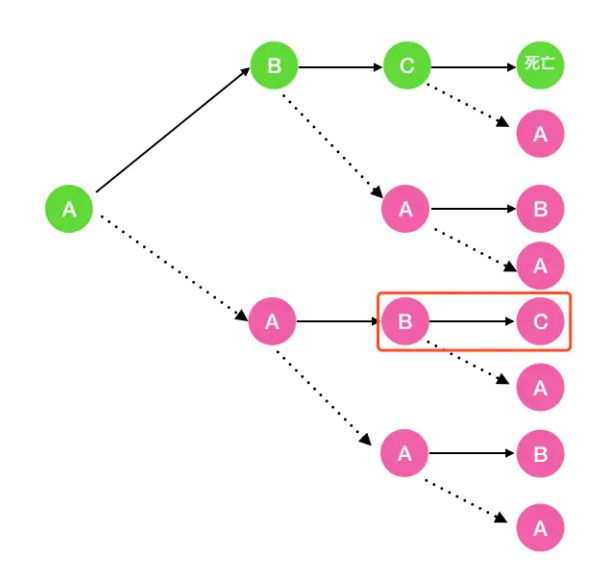
f b(n) 呢,看下图可知 f b(n) = f a(n-1)。 当 n = 1 时 f b(n) = 0。
f c(n) 呢,看下图可知 f c(n) = f b(n-1)。当 n = 1,2 时 f c(n) = 0。
综上, 我们得出的递归公式如下
f(n) = f a(n) + f b(n) + f c(n)
3、根据以上的递归公式我们补充一下函数的功能
int allCells(int n) {
return aCell(n) + bCell(n) + cCell(n);
}
/**
* 第 n 小时 a 状态的细胞数
*/
int aCell(int n) {
if(n==1){
return 1;
}else{
return aCell(n-1)+bCell(n-1)+cCell(n-1);
}
}
/**
* 第 n 小时 b 状态的细胞数
*/
int bCell(int n) {
if(n==1){
return 0;
}else{
return aCell(n-1);
}
}
/**
* 第 n 小时 c 状态的细胞数
*/
int cCell(int n) {
if(n==1 || n==2){
return 0;
}else{
return bCell(n-1);
}
}
只要思路对了,将递推公式转成代码就简单多了,另一方面也告诉我们,可能一时的递归关系我们看不出来,此时可以借助于画图来观察规律。
4、求时间复杂度
由第二步的递推公式我们知道:
f(n) = 2aCell(n-1) + 2aCell(n-2) + aCell(n-3)
之前青蛙跳台阶时间复杂度是指数级别的,而这个方程式显然比之前的递推公式(f(n) = f(n-1) + f(n-2)) 更复杂的,所以显然也是指数级别的。
总结
大部分递归题其实还是有迹可寻的, 按照之前总结的解递归的四个步骤可以比较顺利的解开递归题,一些比较复杂的递归题我们需要勤动手,画画图,观察规律,这样能帮助我们快速发现规律,得出递归公式,一旦知道了递归公式,将其转成递归代码就容易多了,很多大厂的递归考题并不能简单地看出递归规律,往往会在递归的基础上多加一些变形,不过万遍不离其宗,我们多采用自顶向下的分析思维,多练习,相信递归不是什么难事
递归函数调用栈
我们经常可以在书上可以看到,如果递归的深度过大,算法的空间复杂度会很大,甚至会导致栈溢出。这又是为什么。接下来我们使用反汇编的方法,通过绘制堆栈图,来看看递归是怎样占用栈空间的。
小编本次用的为window系统,采用Intel汇编语法格式,使用的是32位的编译器。当然,64位的也差不多。
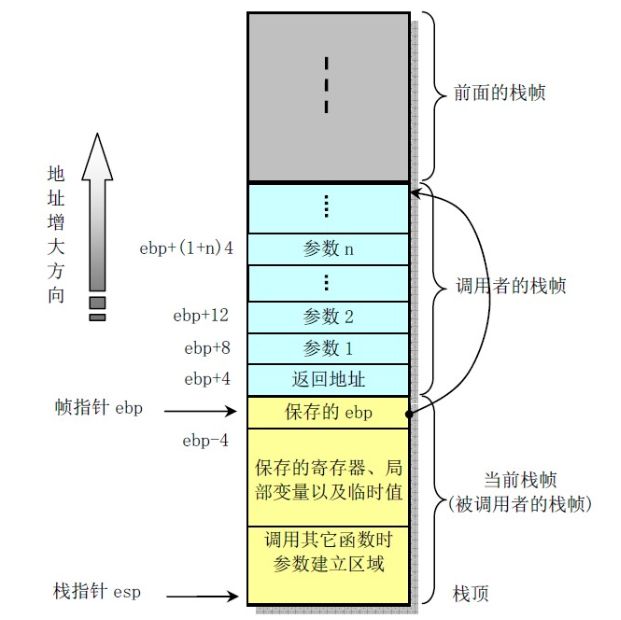
函数每次被调用时,要在调用栈(call stack)上占用一段空间,在这段空间上保存调用者栈帧的基址(ebp)、本函数的局部变量、调用其他函数时的返回地址,并在需要时保存调用者使用的寄存器值,被调函数结束后esp上移表示释放这段空间,然后回到调用者的占用的空间与代码位置继续执行,函数运行阶段在调用栈上占用的这段空间就叫做栈帧,是编译原理运行时空间组织中活动记录(activation record)的一种实现。
栈帧主要通过 ebp、esp 两个寄存器维护,ebp 始终指向栈底,esp 始终指向栈顶。
每个函数被调用时执行下面两条命令:
push ebp; ebp入栈,保存调用者的栈帧基址,以便返回
mov ebp,esp; 将当前 esp 的位置作为当前栈帧的基址
这样在当前栈帧向上一栈帧退回时,只需要取出之前压栈的基址
另一方面,调用过程的指令 call
call a_func
会将 call 指令的下一条指令地址压栈,a_func 函数返回时执行指令。
mov esp,ebp
pop ebp
ret ;返回到 call 压栈保存的地址, 即调用 a_func 的函数中
这样被调函数返回调用函数前就可以将 ebp、esp 置回调用函数的栈帧位置,并返回 call 指令的下一条指令执行。
此外,在 call 指令前,主调函数会将被调函数的参数保存到栈上,因此栈帧的图像如下图所示:
这里我们先编写个递归实现斐波那契数列的C++程序,并插入相对应的断点。
#include
using namespace std;
int Fib(int n)
{
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
Fib(2); //在该处设置断点,进行调试
return 0;
}
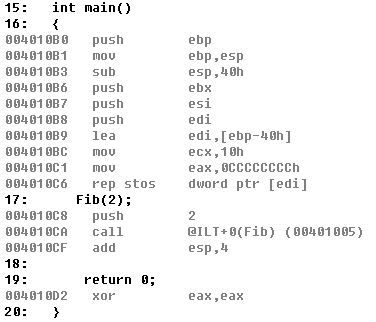
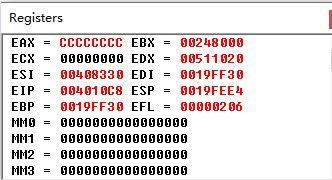
下面是对应程序的反汇编代码以及寄存器当前存放的值的图片:
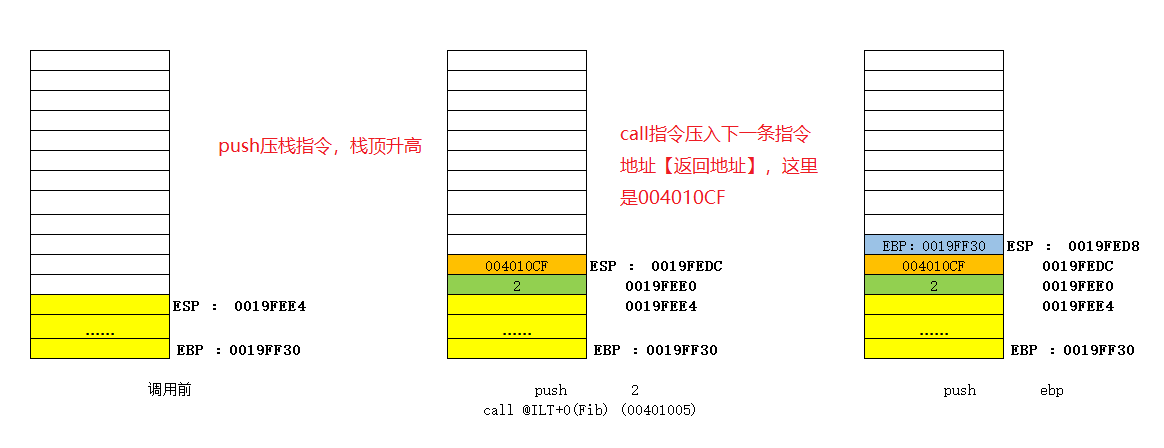
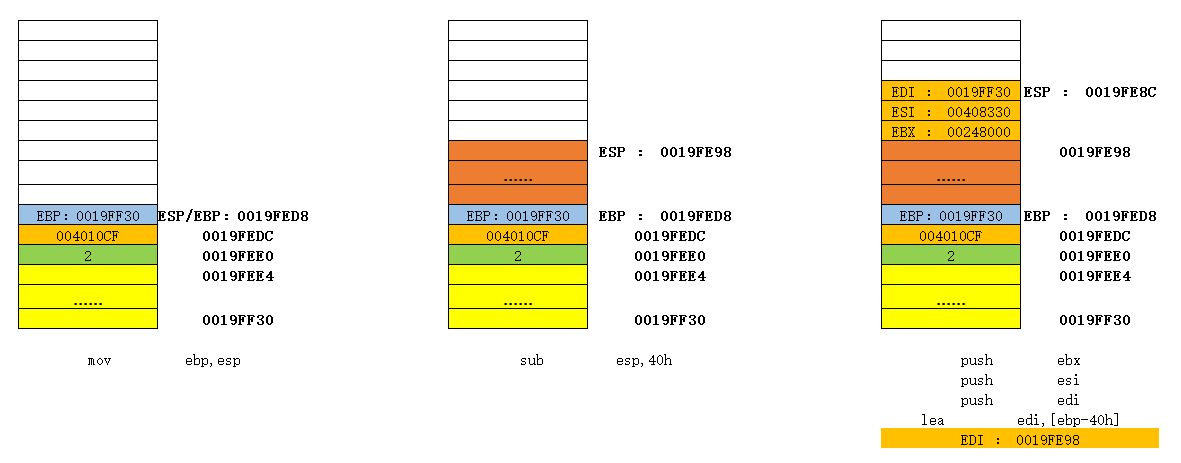
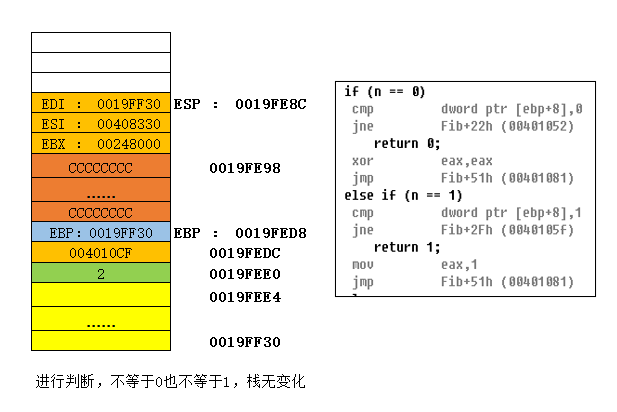
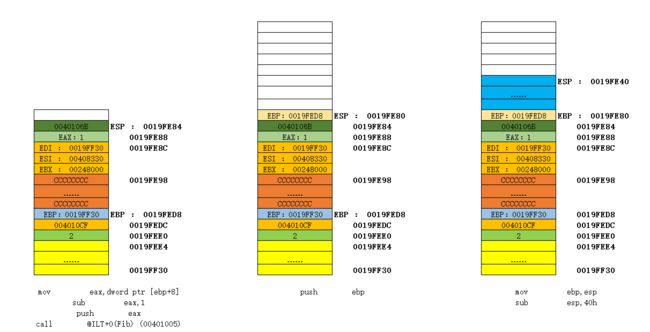
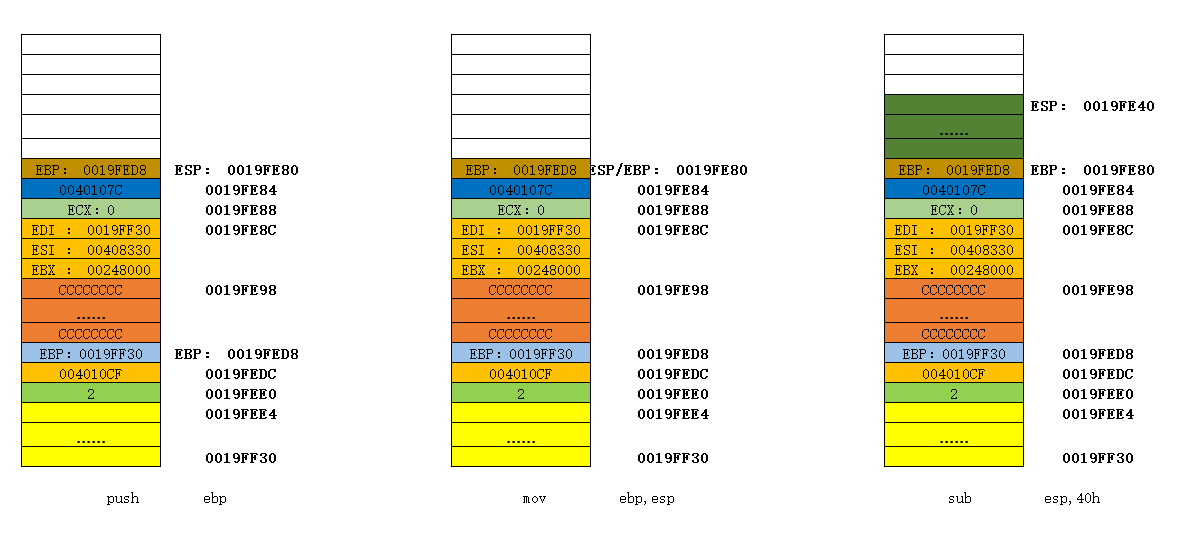
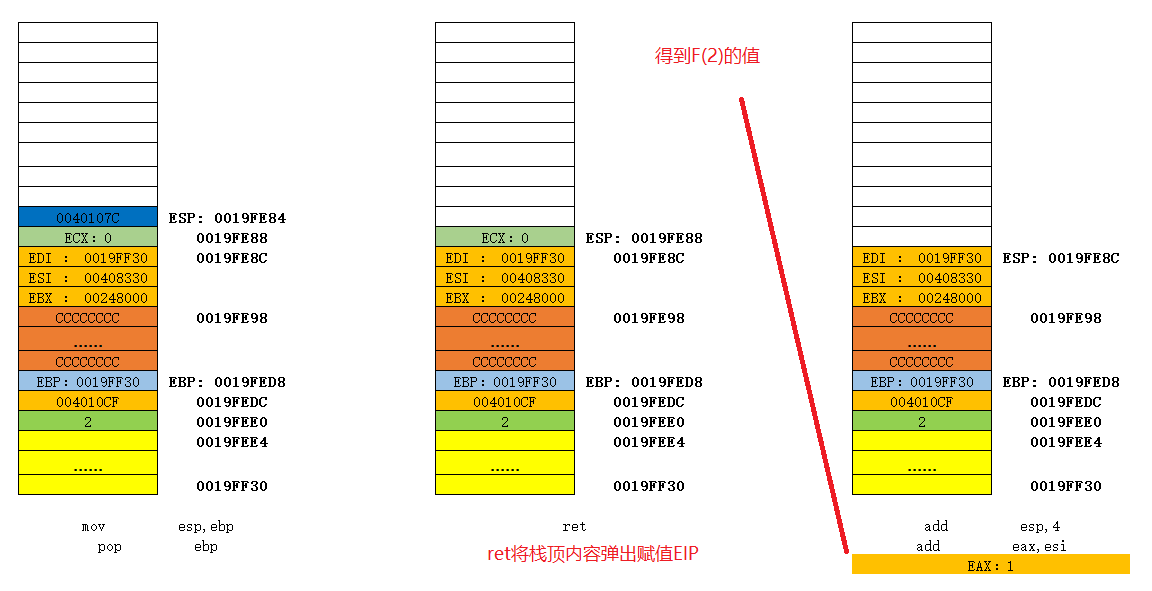
这里以Fib(2)为例,来绘制栈图。相关的X86汇编指令这里不做过多解释。多图如下:
上述图片展示了一个最简单的递归求解Fib(2)的过程。随着我们求解n的值越大,我们可以发现,会进行多次Fib(n)的调用,直到Fib(0)或者Fib(1)才会开始释放栈空间。此时可以发现程序占用的栈空间会越来越大。而我们程序运行时的栈空间是由操作系统还有编译器指定大小的,如果超过这个空间大小,便会出现所谓的 “栈溢出”。因此我们在使用递归算法的时候,要注意降低递归的深度。
递归算法时间复杂度分析与求解
在算法的分析中,当一个算法中包含递归调用时,其时间复杂度的分析会转化成为一个递归方程的求解。而对递归方程的求解,方法多种多样,不一而足。本文主要介绍目前主流的方法:代入法,迭代法,公式法,递归树法。
代入法
实质上就是数学归纳法,先对一个小的值做假设,然后推测更大的值得正确性。
1、猜测解的形式;
2、用数学归纳法求出解中的常数,并证明解是正确的。
(一)求解递归式T(n) = 2T(n/2)+n
我们猜测解是O(nlgn),我们要寻找到一个常数c,使得T(n)<=cnlgn
即T(n) <= 2c(n/2)lg(n/2)+n <= cnlgn-cnlg2+n = cnlgn-cn+n
只要c>=1,T(n)<=cnlgn,所以我们的猜测是正确的。
(二)求解递归式T(n) =T(n)=4T(n/2)+n
我们首先预测时间复杂度为O(n3),,我们要寻找到一个常数c,使得T(n)<=cn3
即T(n) <= 4T(n/2)+n<=4c(n/2)3+n=(c/2)n3+n=cn3-((c/2)n3-n)
只要c>=2以及n>=1,T(n)=O(n3),所以我们的猜测是正确的。
要注意的是,代入法全凭经验,通常用递归树来确定上界,然后用代入法再证明。
迭代法
迭代法就是迭代的展开方程的右边,直到没有可以迭代的项为止,这时通过对右边的和进行估算来估计方程的解。比较适用于分治问题的求解,为方便讨论起见,给出其递归方程的一般形式:
【举 例】T(n)=2T(n/2)+n2
到这里我们知道该算法的时间复杂度为O(n 2),上面的计算中,我们可以直接使用无穷等比数列的公式,不用考虑项数i的约束,实际上这两种方法计算的结果是完全等价的,有兴趣的同学可以自行验证。
公式法
这个方法针对形如:T(n) = aT(n/b) + f(n)的递归方程。这种递归方程是分治法的时间复杂性所满足的递归关系,即一个规模为n的问题被分成规模均为n/b的a个子问题,递归地求解这a个子问题,然后通过对这a个子问题的解的综合,得到原问题的解。这种方法是对于分治问题最好的解法。
对于上述类型的递推公式,我们有以下结论来对其阶进行估计:首先我们根据f(n)的形式不同分成以下两种不同的情况其中c,d为常数:
(1)f(n)=c
(2)f(n)=cnd
首先考虑f(n)=c
对于情况f(n)=cnd
【举例】T(n) = 2T(n/2)+n
根据观察,可以得到a=2,b=2,f(n)=n,故c=1,d=1;
因为log ba=d,代入公式可得T(n)=O(nlog n)
递归树法
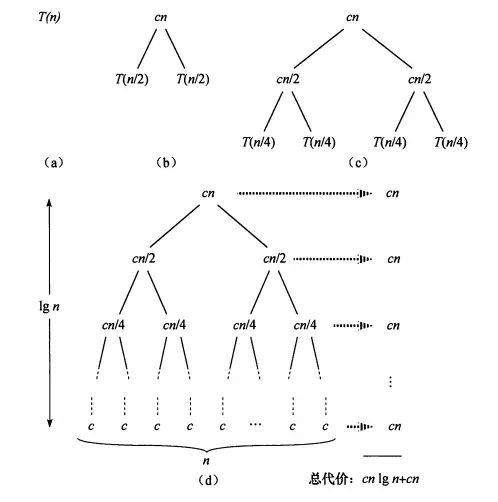
递归树是一棵结点带权值的树。初始的递归树只有一个结点,它的权标记为T(n)。然后按照递归树的迭代规则不断进行迭代,每迭代一次递归树就增加一层,直到树中不再含有权值为函数的结点【即叶节点都为T(1)】。下面以递归方程来讲述递归树的迭代原则。
第一步:把根结点T(n)用根是cn,左节点为T(n/2)、右节点为T(n/2)的子树替代。(即:以分解、合并子问题需要的代价为根,分解得到的子问题为叶的子树。其中常量c代表求解规模为1的问题所需的时间);如下图中的(a)—(b)
第二步:把叶结点按照“第一步”的方式展开;T(n/2)用根是cn/2,左节点为T(n/4),右节点为T(n/4)的子树替代
第三步:反复按照“第一步”的方式迭代,每迭代一次递归树就增加一层,直到树中不再含有权值为函数的结点(即叶结点都为T(1))
在得到递归树后,将树中每层中的代价求和,得到每层代价,然后将所有层的代价求和,得到所有层次的递归调用的总代价。在上图中,完全展开的递归树高度为lgn(树高为根结点到叶结点最长简单路径上边的数目)。所以递归树具有lgn+1层。总代价为cn*(lgn+1)。所以时间复杂度为O(nlgn)。
总结:递归树模型求解递归方程,本质上就是迭代思想的应用,利用递归方程迭代展开过程构造对应的递归树,然后把每层的时间代价进行求和。不过递归树模型更直观,同时递归树也克服了二阶及更高阶递推方程不方便迭代展开的痛点。
整理的很多知识点,在这个过程小编自己也是重新学习了一边有关知识,感概万千!
参考:
1、【算法导论】算法分析:递归式的三种求解方法
2、一文看懂递归
3、x86函数调用过程与栈帧