数据挖掘大作业之实现K-Means,K-Means++,Minibatch-KMeans

数据挖掘大作业之实现K-Means,K-Means++,Minibatch-KMeans

主要参考：https://www.cnblogs.com/huangyc/p/10224045.html，sklearn库。。。

定义：K-means：一种聚类算法，属于基于中心的聚类算法，无监督学习。

解释：已知数据可以通过聚类（或者初步试验观察确定可以聚类）；我们只知道数据分几类（超参数只有1个，即簇的数量）

KMeans实现：

1. 随机创建k个点作为起始质心
2. 计算每一个数据点到k个质心的距离。把这个点归到距离最近的哪个质心。
3. 根据每个质心所聚集的点，重新更新质心的位置。
4. 重复2，3，直到前后两次质心的位置的变化小于一个阈值。
5. 重复2，3，4，实现多次聚类,选择误差最小的一次

具体代码：

• 初始化函数：

    def __init__(self, n_clusters=8, n_init=10, tol=1e-4, init='random', max_iter=300):
        self.k = n_clusters  # 簇数
        self.tol = tol  # 停止聚类阈值
        self.max_iter = max_iter  # 最大迭代次数
        self.n_init = n_init  # 多次聚类，选择最好的一次
        self.init = init # 什么聚类模型

1. 随机创建k个点作为起始质心

# 初始化中心质点
def _init_centroids(self, X):
    n_samples = X.shape[0]
    centers = []
    if self.init == 'random':
        # 返回np.random使用的RandomState单例
        random_state = check_random_state(None)
        seeds = random_state.permutation(n_samples)[:self.k]
        centers = X[seeds]
        return np.array(centers)

check_random_state函数为sklearn库中的函数。

如果seed为None，则返回np.random使用的RandomState单例。如果seed是一个int，则返回一个以seed种子的新RandomState实例。如果种子已经是RandomState实例，则将其返回。否则引发ValueError。

random_state就是为了保证程序每次运行都分割一样的训练集和测试集。否则，同样的算法模型在不同的训练集和测试集上的效果不一样。**

def check_random_state(seed):
    """Turn seed into a np.random.RandomState instance

    Parameters
    ----------
    seed : None | int | instance of RandomState
        If seed is None, return the RandomState singleton used by np.random.
        If seed is an int, return a new RandomState instance seeded with seed.
        If seed is already a RandomState instance, return it.
        Otherwise raise ValueError.
    """
    if seed is None or seed is np.random:
        return np.random.mtrand._rand
    if isinstance(seed, numbers.Integral):
        return np.random.RandomState(seed)
    if isinstance(seed, np.random.RandomState):
        return seed
    raise ValueError('%r cannot be used to seed a numpy.random.RandomState'
                     ' instance' % seed)

5. 重复2，3，4，实现多次聚类，选择误差最小的一次

    def fit(self, X, y=None):
        # 按列求平均
        variances = np.var(X, axis=0)
        # 停止聚类阈值
        self.tol = np.mean(variances) * self.tol  # 把tol和dataset相关联
        # 误差
        bestError = None
        # 中心点
        bestCenters = None
        # 标签
        bestLabels = None
        # 生成质心
        centers = self._init_centroids(X)
        # 进行多次聚类
        for i in range(int(self.n_init)):
            # 实现一次聚类
            labels, centers, error = self.update_centers_labels_error(X, centers)
            if bestError is None or error < bestError:
                bestError = error
                bestCenters = centers
                bestLabels = labels
        self.centers = bestCenters
        return bestLabels, bestCenters, bestError

4. 重复2，3，直到前后两次质心的位置的变化小于一个阈值。

    def update_centers_labels_error(self, X, centers):
        # 误差
        bestError = None
        # 中心点
        bestCenters = None
        # 标签
        bestLabels = None
        # 计算centers的偏移量
        centersShiftTotal = 0
        for i in range(int(self.max_iter)):
            oldCenters = centers.copy()
            # 分配每个点到最近的center
            labels, error = self.update_labels_error(X, centers)
            # 计算新的质心
            centers = self.update_centers(X, labels)
            if bestError is None or error < bestError:
                bestLabels = labels.copy()
                bestCenters = centers.copy()
                bestError = error
            # 矩阵整体元素平方和，不保留矩阵二维特性
            centersShiftTotal = np.linalg.norm(oldCenters - centers) ** 2
            if centersShiftTotal <= self.tol:
                break
        # centers比labels和error多更新一次，再次更新labels,error
        if centersShiftTotal > 0:
            bestLabels, bestError = self.update_labels_error(X, bestCenters)
        return bestLabels, bestCenters, bestError

子函数：

2. 计算每一个数据点到k个质心的距离。把这个点归到距离最近的哪个质心。

# 更新labels和error
    # 计算点与质心的距离，若点与某质心的距离最近，将该点标记为这个集合中的样本
    def update_labels_error(self, X, centers):
        # 分配每个点到最近的center
        labels = []
        for point in X:
            shortest = float("inf")  # 正无穷
            shortest_index = 0
            for i in range(len(centers)):
                # 计算欧几里得距离
                val = np.sqrt(np.sum(np.square(point[np.newaxis] - centers[i])))
                if val < shortest:
                    shortest = val
                    shortest_index = i
            labels.append(shortest_index)
        # 计算误差
        new_means = defaultdict(list)
        error = 0
        for assignment, point in zip(labels, X):
            new_means[assignment].append(point)
        for points in new_means.values():
            newCenter = np.mean(points, axis=0)
            error += np.sqrt(np.sum(np.square(points - newCenter)))
        return labels, error

3. 根据每个质心所聚集的点，重新更新质心的位置。

# 更新中心点
    def update_centers(self, X, labels):
        new_means = defaultdict(list)
        centers = []
        for assignment, point in zip(labels, X):
            new_means[assignment].append(point)
        for points in new_means.values():
            newCenter = np.mean(points, axis=0)
            centers.append(newCenter)
        return np.array(centers)

KMeans++

如何选取初始质心的位置，

如果仅仅是完全随机的选择，有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。

K-Means++的对于初始化质心的优化策略也很简单，如下：

1. 从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1.
2. 对于数据集中的每一个点xi，计算它与已选择的聚类中心中最近聚类中心的距离.

D(xi)=argmin|xi−μr|2 r=1,2,…kselected ，计算距离和

3. 选择一个新的数据点作为新的聚类中心，选择的原则是：距离和较小的先，被选为中心点
4. 重复2和3直到选择出k个聚类质心。
5. 利用这k个质心来作为初始化质心去运行标准的K-Means算法。

代码实现：

初始化函数：

    def __init__(self, n_clusters=8, max_iter=300, init='k-means++', tol=1e-4):
        super(KMeansPlusPlus, self).__init__(
            n_clusters=n_clusters, max_iter=max_iter, tol=tol
        )
        self.init = init

重写初始化中心点函数：

    def _init_centroids(self, X):
        n_samples = X.shape[0]
        centers = []
        if self.init == 'random':
            # 返回np.random使用的RandomState单例
            random_state = check_random_state(None)
            seeds = random_state.permutation(n_samples)[:self.k]
            centers = X[seeds]
        elif self.init == 'k-means++':
            centers = self.k_means_plus_plus(X)
        return np.array(centers)

k-means++中心点的初始化：

# kmeans++的初始化方式，加速聚类速度
    def k_means_plus_plus(self, X):
        # 样本数量，特征数量
        n_samples, n_features = X.shape
        # 随机产生中心点
        centers = np.empty((self.k, n_features))
        # n_local_trails是选择候选点的个数
        n_local_trials = 2 + int(np.log(self.k))
        # 产生第一个随机点
        random_state = check_random_state(None)
        center_id = random_state.randint(n_samples)
        centers[0] = X[center_id]
        # closet_dist_sq是每个样本，到所有中心点最近距离，为一个数组
        # 假设现在有m个中心点，closest_dist_sq = [min(样本1到m个中心距离),min(样本2到m个中心距离),...min(样本n到m个中心距离)]
        closet_dist_sq = np.sqrt(np.sum(np.square(centers[0, np.newaxis] - X), axis=1))
        # 所有最短距离的和
        current_pot = closet_dist_sq.sum()
        for c in range(1, self.k):
            # 生成n_local_trails个随机地址，范围为[0,1）的随机数，并映射到current_pot的长度
            rand_vals = random_state.random_sample(n_local_trials) * current_pot
            # np.cumsum([1,2,3,4])=[1,3,6,10]:累加当前索引前面的值
            # np.searchsorted搜索随机出的rand_vals落在cumsum(closet_dist_sq)中的位置
            # candidate_ids候选节点的索引
            candidate_ids = np.searchsorted(np.cumsum(closet_dist_sq), rand_vals)

            # 最好的候选节点：计算出的距离和最小
            best_candidate = None
            # 最好的候选节点计算出的距离和
            best_pot = None
            # 最好的候选节点计算出的距离列表
            best_dist_sq = None
            for trial in range(n_local_trials):
                # 计算每个样本到候选节点的欧式距离
                distance_to_candidate = np.sqrt(np.sum(np.square(X[candidate_ids[trial]] - X), axis=1))
                # 计算每个候选节点的距离序列new_dist_sq
                new_dist_sq = np.minimum(closet_dist_sq, distance_to_candidate)
                # 计算每个候选节点的距离总和new_pot
                new_pot = new_dist_sq.sum()
                # 选择最小的new_pot
                if (best_candidate is None) or (new_pot < best_pot):
                    best_candidate = candidate_ids[trial]
                    best_pot = new_pot
                    best_dist_sq = new_dist_sq
            centers[c] = X[best_candidate]
            current_pot = best_pot
            closet_dist_sq = best_dist_sq
        return centers

MiniBatchKMeans

在统的K-Means算法中，要计算所有的样本点到所有的质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的K-Means算法非常的耗时，就算加上elkan K-Means优化也依旧。在大数据时代，这样的场景越来越多。此时Mini Batch K-Means应运而生。

顾名思义，Mini Batch，也就是用样本集中的一部分的样本来做传统的K-Means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。

在Mini Batch K-Means中，我们会选择一个合适的批样本大小batch size，我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的？一般是通过无放回的随机采样得到的。

为了增加算法的准确性，我们一般会多跑几次Mini Batch K-Means算法，用得到不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。

思想：

Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了k-均值的收敛时间，小批量k-均值产生的结果，一般只略差于标准算法。

迭代步骤：
1：从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心
2：更新质心
与K均值算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算

代码实现：

初始化函数：

    def __init__(self, n_clusters=8, max_iter=300, init='minibatch', batch_size=100, tol=1e-4):
        super(MMiniBatchKMeans, self).__init__(
            n_clusters=n_clusters, max_iter=max_iter, tol=tol
        )
        self.batch_size = batch_size  # 采样数据集的大小
        self.init = init

重写初始化中心点函数：

    def minibatch(self, X):
        # 样本数量，特征数量
        n_samples, n_features = X.shape
        random_state = check_random_state(None)
        validation_indices = random_state.randint(0, n_samples, self.batch_size)
        X_valid = X[validation_indices]
        return self.k_means_plus_plus(X_valid)

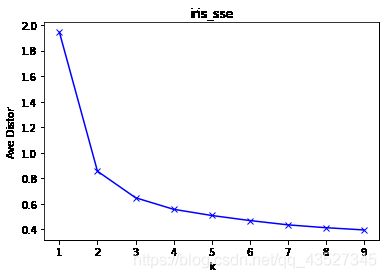
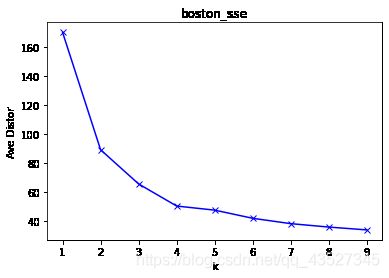
手肘法

确定簇数

SSE=∑i=1k∑x∈Ci|x−μi|2

指定一个Max值，即可能的最大类簇数。然后将类簇数K从1开始递增，一直到Max，计算出Max个SSE。根据数据的潜在模式，当设定的类簇数不断逼近真实类簇数时，SSE呈现快速下降态势，而当设定类簇数超过真实类簇数时，SSE也会继续下降，当下降会迅速趋于缓慢。通过画出K-SSE曲线，找出下降途中的拐点，即可较好的确定K值。

代码：

import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt# dataName = "iris"
X=datasets.load_iris().data
dataName = "boston"
# X=datasets.load_boston().data
# y_true = datasets.load_boston().target
y_true = datasets.load_iris().target
#降维
tsne = TSNE(n_components=2, init='pca', random_state=0)
# 对部分数据先拟合fit，找到该part的整体指标，如均值、方差、最大值最小值等等（根据具体转换的目的），然后对该trainData进行转换transform，从而实现数据的标准化、归一化等等。
X_tsne = tsne.fit_transform(X)

K = range(1, 10)
# print(X)
meandistortions = []
meandistortions1 = []
for k in K:
    kmeans = KMeansBase(n_clusters=k)
    centers = kmeans.fit(X)[1]
    error=sum(np.min(cdist(X,centers, 'euclidean'), axis=1))
    meandistortions.append(error)
    '''
    # cdist(X, kmeans.cluster_centers_, 'euclidean')  求出X到cluster_centers_之间的距离
    #np.min(cdist(X,kmeans.cluster_centers_, 'euclidean'), axis=1)   按行的方向，对每一行求出一个最小值
    #sum(np.min(cdist(X,kmeans.cluster_centers_, 'euclidean'), axis=1)) 求出每次得到最小值列表的和
    # 求出每次最小值列表和的平均值
    '''
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    error=sum(np.min(cdist(X,kmeans.cluster_centers_, 'euclidean'), axis=1))
    meandistortions1.append(error / X.shape[0])
print(meandistortions)
print(meandistortions1)
plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k')
# plt.ylabel('平均畸变程度',fontproperties=font)
plt.ylabel('Ave Distor')
# plt.title('用肘部法则来确定最佳的K值',fontproperties=font);
# plt.title('digits_sse');
plt.savefig("iris1.png",bbox_inches='tight')
plt.show()
plt.plot(K, meandistortions1, 'bx-')
plt.xlabel('k')
# plt.ylabel('平均畸变程度',fontproperties=font)
plt.ylabel('Ave Distor')
# plt.title('用肘部法则来确定最佳的K值',fontproperties=font);
# plt.title('digits_sse');
# plt.savefig("digits_sse.png",bbox_inches='tight')
plt.show()

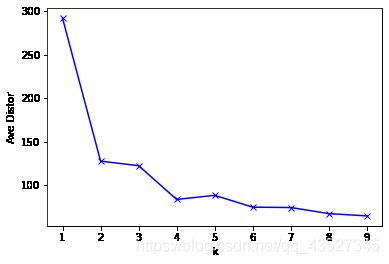
这里与标准库输出的手肘法不一样，应该是因为kmeandbase的误差跳出出现了问题。导致在分类簇数比较多时，曲线出现了较大的问题
iris,k=3

boston,k=4

digits，k=10

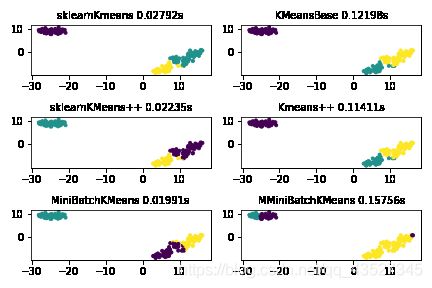
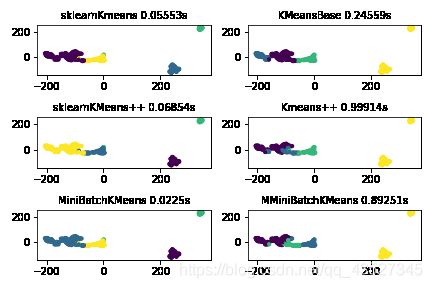
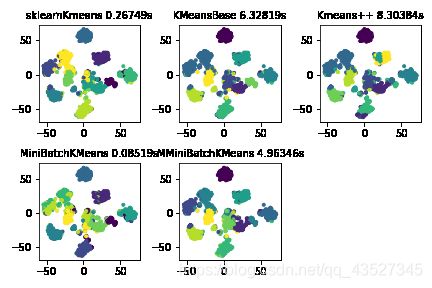
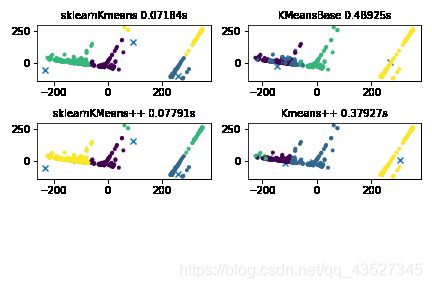
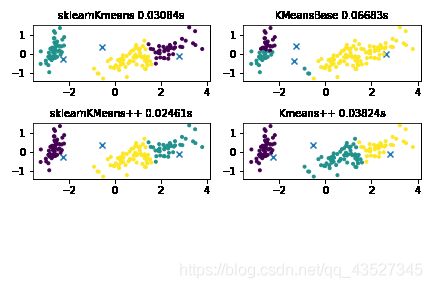
三个模型对比

三个模型三个数据集实现对比：

allData = {
     "iris":datasets.load_iris().data, "boston":datasets.load_boston().data, "digits":datasets.load_digits().data}
models = {
     "sklearnKmeans":KMeans,"KMeansBase":KMeansBase,"sklearnKMeans++":KMeans,"Kmeans++":KMeansPlusPlus,"MiniBatchKMeans":MiniBatchKMeans,"MMiniBatchKMeans":MMiniBatchKMeans}
# models = {"sklearnKmeans":KMeans,"KMeansBase":KMeansBase,"sklearnKMeans++":KMeans,"Kmeans++":KMeansPlusPlus}

for dataName, value in allData.items():
    subplot_counter=0
    png_number=1
    file_counter=1
    n_clusters = 3
    if dataName == "boston":
        n_clusters = 4
    if dataName == "digits":
        n_clusters = 10
    #降维
    # 主成分分析是由因子分析进化而来的一种降维的方法，通过正交变换将原始特征转换为线性独立的特征，转换后得到的特征被称为主成分。主成分分析可以将原始维度降维到n个维度，有一个特例情况，就是通过主成分分析将维度降低为2维，这样的话，就可以将多维数据转换为平面中的点，来达到多维数据可视化的目的。
    pca = decomposition.PCA(n_components=2)
    # t-SNE(t分布随机邻域嵌入)是一种用于探索高维数据的非线性降维算法。通过基于具有多个特征的数据点的相似性识别观察到的簇来在数据中找到模式，将多维数据映射到适合于人类观察的两个或多个维度。
    tsne = TSNE(n_components=2, init='pca', random_state=0)

    X_tsne = tsne.fit_transform(value)
#     X_tsne = pca.fit_transform(value)
    for modelName, model in models.items():
    #         print("dataset=%s model=%s takeTime=%s"%(dataName, modelName, round(takeTime, 5)))
        startTime = time.time()
        if modelName == "sklearnKMeans++":
            init = "k-means++"
            model=model(n_clusters = n_clusters, init=init)
        else:
            model=model(n_clusters = n_clusters)
        if modelName == "KMeansBase" or modelName == "MMiniBatchKMeans" or modelName=="Kmeans++":
            centers = model.fit(value)[1]
            labels = model.predict(value)
        else:
            labels = model.fit_predict(value)
            centers=model.cluster_centers_

        takeTime = time.time() - startTime
        print("dataset=%s model=%s takeTime=%s"%(dataName, modelName, round(takeTime, 5)))

        subplot_counter += 1
        plt.subplot(3, 2, subplot_counter)
        centers_tsne = tsne.fit_transform(centers)
    #     print(centers)
#         centers_tsne = pca.fit_transform(centers)
#         plt.scatter(centers_tsne[:, 0],centers_tsne[:, 1], marker='x')
        plt.scatter(X_tsne[:, 0],X_tsne[:, 1], c=labels, marker='.')
        plt.title("%s %ss"%(modelName, round(takeTime, 5)),fontsize=10)
    plt.tight_layout() 
    plt.savefig(dataName+".png")
    plt.show()

• t-SNE(t分布随机邻域嵌入)是一种用于探索高维数据的非线性降维算法。通过基于具有多个特征的数据点的相似性识别观察到的簇来在数据中找到模式，将多维数据映射到适合于人类观察的两个或多个维度。

通过对比可以看出：KMeans++的运行时间比原始的kmeans短，minibatchKmeans的运行时间有时比kmeans++长，有时短，应该是因为：minibatchKmeans采取随机抽样的方法，随机抽取了100个样本，运行时间会短，但是随机抽样会导致抽样不均匀的问题，可能会导致寻找中心点时间加长。对于大数据集而言，可以多运行几次，找到运行效果最好的一次

iris

boston

digits

通过对比可以看出：KMeans++的运行时间比原始的kmeans短，minibatchKmeans的运行时间有时比kmeans++长，有时短，应该是因为：minibatchKmeans采取随机抽样的方法，随机抽取了100个样本，运行时间会短，但是随机抽样会导致抽样不均匀的问题，可能会导致寻找中心点时间加长。对于大数据集而言，可以多运行几次，找到运行效果最好的一次

• 主成分分析是由因子分析进化而来的一种降维的方法，通过正交变换将原始特征转换为线性独立的特征，转换后得到的特征被称为主成分。主成分分析可以将原始维度降维到n个维度，有一个特例情况，就是通过主成分分析将维度降低为2维，这样的话，就可以将多维数据转换为平面中的点，来达到多维数据可视化的目的。

iris

这里kmeansbase的中心点为训练后的中心点，发现它没有迭代成功，和sklearn库的不一样。迭代误差时
跳出条件有问题
boston

digits