人工智能——神经网络【1】基本了解

人工智能——神经网络【1】基本了解（感知非常简单有趣的案例）

在经历了古典控制理论和现代控制理论的学习后，转到了智能控制的相关课程学习，但学着学着感觉课堂的内容相对于整个框架体系而言太少太少，所以想着能自己扩展一些，等这阶段对一些底子技巧打好后，就开始出一些机器学习深度学习的文章与大家伙共同学习。本篇博文主要是对神经网络进行一定的感知，不讲太多的原理，重在体验效果，程序均可以跑，跑不出来评论或者私聊我~（我用的matlab2019b版本）
1. 神经网络的基本认识
我们知道神经网络就是模拟生物神经系统的，由一个个神经元构成，那么我们看一下基本的神经元模型：

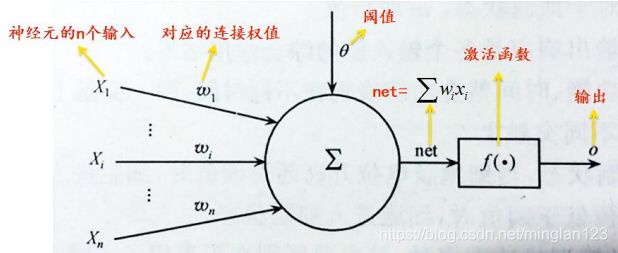
中间的圆就是“元”，神经元的输入为X序列，连接权值表示的是对输入的一个量化大小，权值越大也就意味着在这个神经元中该权值所对应的输入也就越重要，求和之后再和阈值相比较（非必要），通过激励函数输出，激励函数的类型也有很多例如sgn函数，来得到最后输出的实际值。
那么对于神经元构成的网络模型：

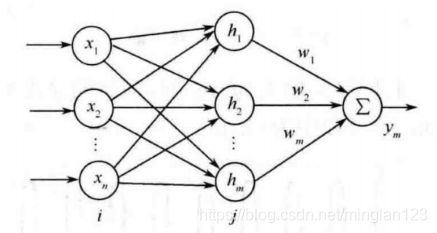
网络模型也是有很多的类型，包括前向型、反馈型和自组织型等，那么对于这些类型本篇博文不再详细介绍，因为是感知嘛，所以等会尽快进入实例，那么首先对于大多数介绍文中的神经网络图我觉得不如这一张感知强烈，RBF模型，左边的几个圈是输入层，中间的是隐藏层，m是隐藏节点数，右边的是输出层，这个模型只有一个输出。对于这个模型，我们是否可以理解为这样的一种形式：输入层我给出什么类型的原料，最后输出一个到底是什么类型的成品。所以神经网络有时候也可以认为是一个黑匣子，那么对于这样的黑匣子，我们下面对他感知一下吧。
2.隐藏层、隐藏层节点数的思考
虽说是黑匣子，但我们不得不去考虑一下这个黑匣子的功效，所以需要对隐藏层和隐藏节点数有一点的思考。那么下面通过这样一个例子进行感知（基于MATLAB神经网络工具箱）：

这是一个非线性函数，我们要对它进行逼近，用到的神经网络模型为BP前向型神经网络，k为频率系数，取值为1或2，参数p取值变动范围为：-2~2，步长为0.01.然后编程逼近，在给出具体的程序前，我们也要理解一下什么是学习率：

人工智能里面特别重要的一个概念就是学习，它会与理想值进行对比，从而不断自我修正权重系数，上述就是这个权重修正的公式，里面的α就是学习率，表征它修正速度的权重，所以在下面跑神经网络的时候也需要定义这个参数。

%% 训练数据设置
k=1;%频率系数
p=-2:0.01:2;%步长
y=3*((cos(k*pi*p)).^2);%目标函数
%% BP网络训练
n=10;                   %%隐藏节点数
net=newff(p,y,n);       %%隐含层数目1
% net=newff(p,y,[n,n]); %%两层
%% 网络参数及结果输出
net.trainParam.epochs=1000;       %最大步数设置为1000
net.trainParam.goal=0.00004;      %误差目标为0.00004
net.trainParam.lr=0.1;            %学习率
net=train(net,p,y);               %训练网络
y1=sim(net,p);                    %网络输出
%% 结果分析
figure(1)
plot(p,y1,':og')
hold on
plot(p,y,'-*');
legend('预测输出','期望输出')
title('BP网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
%预测误差
error=y1-y;
figure(2)
plot(p,error,'-*')
title('BP网络预测误差','fontsize',12)
ylabel('误差','fontsize',12)
xlabel('样本','fontsize',12)
figure(3)
plot(p,(y-y1)./y1,'-*');
title('神经网络预测误差百分比')

结果可以自行跑一下尝试一下，可以自行修改学习率、误差目标、k值以及隐藏层或者隐藏层节点数查看一下效果，单层隐藏层情况下，N取3、5、10，可以看到拟合的效果明显不同，修改一下隐藏层节点数和隐藏层数，感知会更明显：

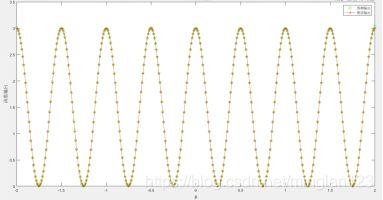
程序运行后会看到网络训练的过程，同时可以得到一下结论：
（1）层数越多，对于整个网络的误差越小，主要体现于最大最小误差，但是整体的训练时间会长，如本例子很简单的拟合，但两层的时候，节点数量过多也会导致较慢的时间。
（2）隐藏点数要小于训练样本数-1，不然可能造成样本与误差的相关性太小，学习的结果没有意义；输入层的节点数同理也小于这个值。
3.动物类型辨识
下面讲一个个人觉得很有意思的案例，就是对动物类型的辨识，早在上个世纪，Kohonen就提出了SOM（自组织型适应网络）的动物分类案例，今天我就来复现一下，和大家一起感受一下神经网络的魅力，既然是感知，就不多说这个网络的原理，大体上可以这样形容：
输入层为我们的各个动物样本，竞争层则是对样本中各个参数进行权重优化，所谓权重优化，就比如一开始的竞争层看做一个平面，左上角有一块很符合牛的属性，那么这一块就会提升权重从而使其更符合牛，训练后，我们知道马的体态和牛很像，所以马也在这个角落附近。总体上就是这样一个过程，这个网络的作用便是能够使属性类似的动物挨在一起，最后可以随便输入一个案例，得到最符合的那一个点，而距离每一个动物所在最优点的距离便是可能是这种动物的可能性大小。下面我们赶紧开始，首先给动物搜索资料给予各个参数：

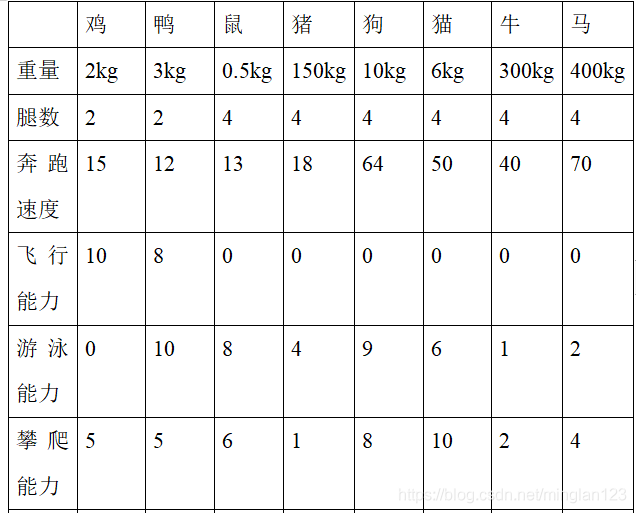
一定！！！一定！！！将这个数据参数在命令行输入一个矩阵然后保存为Mat格式。然后跑代码就好啦~

clear;close all;clc;
%% 录入输入数据
load p1                %加载数据，前提是一定保存为p1这个.mat文件在路径下
inputs = mapminmax(p); %归一化数据
%% 网络建立
M=10;N=10;              %定义竞争层10*10
dimension1 = M; dimension2 = N;
net=newsom(minmax(inputs),[dimension1 dimension2]);
figure,plotsom(net.layers{
     1}.positions);
a=[100,500,1000,2000];
%% 训练网络
net.trainParam.epochs=a(4);      %网络最大迭代次数设置为2000
net = train(net,inputs);         %训练网络
% 测试网络
y = sim(net,inputs);
yc= vec2ind(y);%输出结果
figure,plotsom(net.IW{
     1,1},net.layers{
     1}.distances);
% 网络神经元分布情况
 figure, plotsomtop(net)         %查看网络拓朴学结构
 figure, plotsomnc(net)          %查看临近神经元联系
 figure, plotsomnd(net)          %查看临近神经元直接距离的情况
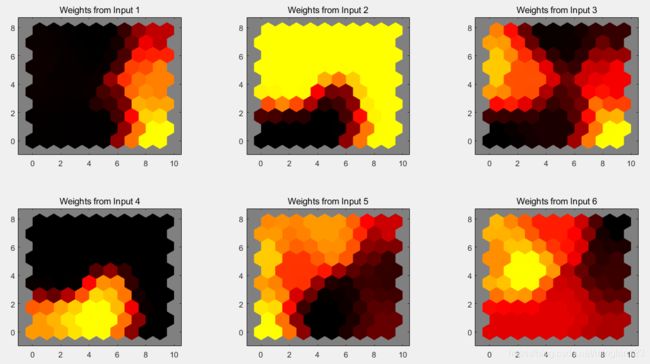
 figure, plotsomplanes(net)      %查看网络权重面
 figure, plotsomhits(net,inputs) %查看每个神经元的分类情况
 figure, plotsompos(net,inputs)  %查看网络权重位置
%% 网络作分类的预测
% 按照该动物的特性输入待测样本
text=[146 4 17 0 4 1];   %参数和猪差不太多的动物
for i=1:6
    text(i)=2*(text(i)-min(p(i,:)))/(max(p(i,:))-min(p(i,:)))-1;
end
text=text';
mingout=mapminmax(text);
r=sim(net,mingout);
% 变换函数 将单值向量转变成下标向量。
rr=vec2ind(r)  %输出结果
%% 输出最后的分类结果
min=100;rrc=0;
for i=1:6
    if abs(yc(i)-rr)鸡','鸭','鼠','猪','狗','猫','牛','马'];
rrcprint(rrc)

输出的结果肯定是猪啦，可以通过改变训练次数来看一下不同的效果，以及通过不同的拓扑结构也可，看一下竞争层的训练结果吧：

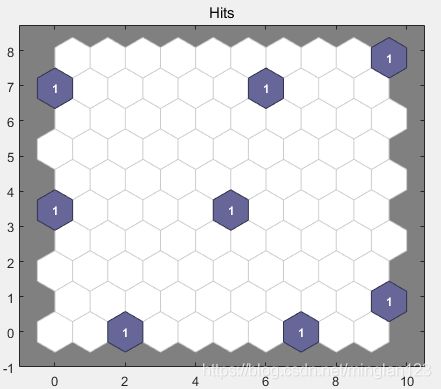
上面的图是各动物所分布的权重中心，下面这个图是各个样本动物的权重分布，深色表示权重越大，也就是每个样本动物的覆盖面。

参考文献
1.关于BP神经网络中输入层、隐藏层、输出层节点数的讨论