基于栈的中缀算术表达式求值_LeetCode算法150. 逆波兰表达式求值
 leetcode
leetcode
LeetCode算法-150. 逆波兰表达式求值
150. 逆波兰表达式求值
题目
根据 逆波兰表示法,求表达式的值。有效的运算符包括 +, -, *, / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:
整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入: ["2", "1", "+", "3", "*"]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
输出: 22
解释: 该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
题解
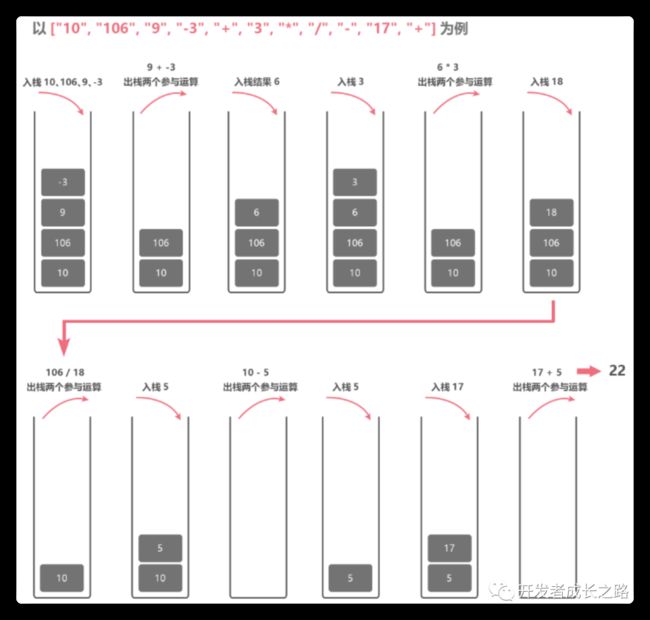
逆波兰式问题一般都是使用栈来解决, 1.定义一个栈,用于保存数字 2.tokens从头部出一个元素 3.如果是操作符号,arrsnum出栈两个元素,并计算这两个元素,得到的结果重新push到数组里面去。4.若果是数字就push到arrsnum里面 5.重复执行 2-5 到tokens里面的元素全部出来即可
Java
public int evalRPN(String[] tokens) {
Stack stack = new Stack<>();
Integer a = 0;
Integer b = 0;for (String s : tokens) {
switch (s) {
case "+":
a = stack.pop();
b = stack.pop();
stack.push(b + a);break;case "-":
a = stack.pop();
b = stack.pop();
stack.push(b - a);break;case "*":
a = stack.pop();
b = stack.pop();
stack.push(b * a);break;case "/":
a = stack.pop();
b = stack.pop();
stack.push(b / a);break;default:
stack.push(Integer.valueOf(s));break;
}
}return stack.pop();
}C++
class Solution {
public:
int evalRPN(vector &tokens) {
int i =0;
bool err = false;
vector exp;
for (int i=0; i if (isNum(tokens[i])) {
exp.push_back(value);
} else if( isOp(tokens[i])==true ) {
if (exp.size() 2) {
return 0; //ERROR
}
int lhs, rhs;
rhs = exp.back();
exp.pop_back();
lhs = exp.back();
exp.pop_back();
int evlValue;
if (tokens[i]=="+"){
evlValue = lhs + rhs;
}else if (tokens[i]=="-"){
evlValue = lhs - rhs;
}else if (tokens[i]=="*"){
evlValue = lhs * rhs;
}else if (tokens[i]=="/"){
evlValue = lhs / rhs;
}
exp.push_back(evlValue);
}else {
return 0; //ERROR
}
}
if (exp.size()==1){
return exp.back();
}
return 0;
}
private:
long value;
bool isOp(string &op) {
return (op=="+" || op=="-" || op=="*" || op=="/");
}
bool isNum(string &num) {
char *end;
value = strtol(num.c_str(), &end, 10);
if (end == num.c_str() || *end != '\0' || errno == ERANGE){
return false;
}
return true;
}
};
更多干货文章
博客:www.qiuxuewei.com
微信公众号:「@开发者成长之路」
「一个没有鸡汤只有干货的公众号」