密码学是区块链中一重大技术组成,在理论框架总结一下,以供后来者学习。
序言
密码学有3个主要目的:加密 Encryption ,认证 Authentication ,识别 Identification
1,加密阻止恶意者读取你的数据
2,认证阻止恶意者在不被发现的情况下改动你的数据
3,识别阻止恶意者假装你
一、哈希
数据摘要算法,或称为哈希算法、散列算法,它能任意长度的二进制值(明文)映射为较短的固定长度的二进制值(Hash值),并且不同的明文很难映射为相同的Hash值。严格来说并不能算是一种加密算法,只能说是一种摘要算法(数据摘要算法是密码学算法中非常重要的一个分支,它通过对所有数据提取指纹信息以实现数据签名、数据完整性校验等功能,由于其不可逆性,有时候会被用做敏感信息的加密。)
特点
一个优秀的 hash 算法,将能实现:
1,正向快速:给定明文和 hash 算法,在有限时间和有限资源内能计算出 hash 值。
2,逆向困难:给定(若干) hash 值,在有限时间内很难(基本不可能)逆推出明文。
3,输入敏感:原始输入信息修改一点信息,产生的 hash 值看起来应该都有很大不同。
4,抗碰撞性:很难找到两段内容不同的明文,使得它们的 hash 值一致。如果给定一个明文前提下,无法找到碰撞的另一个明文,称为“弱抗碰撞性”;如果无法找到任意两个明文,发生碰撞,则称算法具有“强抗碰撞性”。
代表算法
MD5(不够安全),SHA系列(SHA1不够安全,推荐至少使用SHA2-256)
相关概念
数字摘要:
顾名思义,数字摘要是对数字内容进行 Hash 运算,获取唯一的摘要值来指代原始数字内容。 数字摘要是解决确保内容没被篡改过的问题(利用 Hash 函数的抗碰撞性特点)。数字摘要是 Hash 算法最重要的一个用途。在网络上下载软件或文件时,往往同时会提供一个数字摘要值,用户下载下来原始文件可以自行进行计算,并同提供的摘要值进行比对,以确保内容没有被修改过。
二次哈希:
在比特币中,工作量证明和密钥编码过程中多次使用了二次哈希,如SHA(SHA256(k))或者RIPEMD160(SHA256(K)),这种方式带来的好处是增加了工作量或者在不清楚协议的情况下增加破解难度,从安全性角度并没有显著增加(如果是暴力穷举破解的话,需要增加一倍破解时间)。真正的二次哈希是基于加盐的哈希,什么意思呢?对于特定的待散列数据和特定的散列算法,可以知道散列值是一定的,这种情况下如果用散列保护敏感数,那就很容易使用字典攻击反向推算,比如我计算123456的SHA256值就可以反推了,解决办法就是先做一次散列,再加一次随机数据以后再做一次散列,随机数据就是所谓的盐。
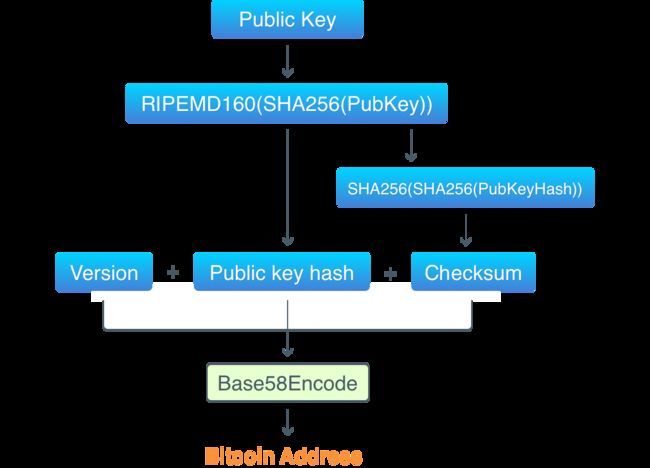
比特币由公钥获取地址过程
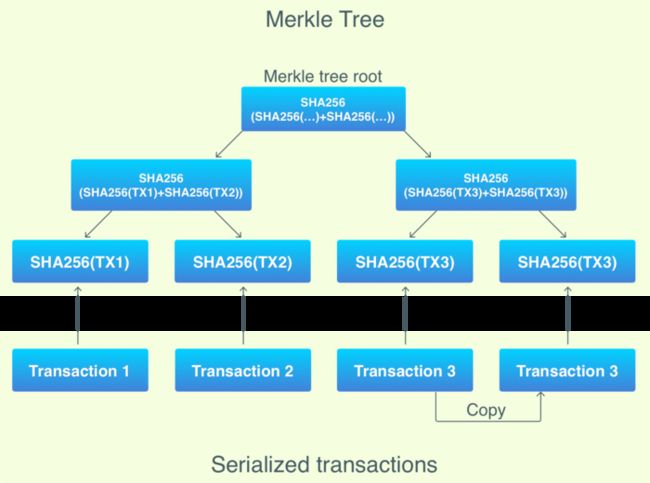
Merkle Tree:
是一种树(数据结构中所说的树),可用于简易支付验证SPV
在比特币中,每个块都会有一个 Merkle 树,它从叶子节点(树的底部)开始,一个叶子节点就是一个交易哈希(比特币使用双 SHA256 哈希)。叶子节点的数量必须是双数,但是并非每个块都包含了双数的交易。因为,如果一个块里面的交易数为单数,那么就将最后一个叶子节点(也就是 Merkle 树的最后一个交易,不是区块的最后一笔交易)复制一份凑成双数。
从下往上,两两成对,连接两个节点哈希,将组合哈希作为新的哈希。新的哈希就成为新的树节点。重复该过程,直到仅有一个节点,也就是树根。根哈希然后就会当做是整个块交易的唯一标示,将它保存到区块头,然后用于工作量证明。
Merkle 树的好处就是一个节点可以在不下载整个块的情况下,验证是否包含某笔交易。并且这些只需要一个交易哈希,一个 Merkle 树根哈希和一个 Merkle 路径。
代码实现
package main
import "crypto/sha256"
//Merkle 树的作用:一个节点可以在不下载整个块的情况下,验证是否包含某笔交易。
// 并且这些只需要一个交易哈希,一个 Merkle 树根哈希和一个 Merkle 路径。
//默克尔树
type MerkleTree struct {
RootNode *MerkleNode
}
//节点
type MerkleNode struct {
Left *MerkleNode
Right *MerkleNode
data []byte
}
//创建默克尔树
func NewMerkleTree(data [][]byte) *MerkleTree {
var nodes []MerkleNode
if len(data) % 2 != 0 { //如果节点数为单数,复制最后一个节点数据并追加
data = append(data, data[len(data) - 1])
}
for _, datum := range data {
node := NewMerkleNode(nil, nil, datum)
nodes = append(nodes, *node)
}
for i := 0; i < len(data)/2; i++ { //一层层向上合并
var newlevel []MerkleNode
for j := 0; j < len(nodes); j += 2 {
node := NewMerkleNode(&nodes[j],&nodes[j+1],nil)
newlevel = append(newlevel, *node)
}
nodes = newlevel
}
mTree := MerkleTree{&nodes[0]}
return &mTree
}
//创建一个节点
func NewMerkleNode(left ,right *MerkleNode, data []byte) *MerkleNode {
mNode := MerkleNode{}
if left == nil && right == nil {
hash := sha256.Sum256(data)
mNode.data = hash[:]
} else {
preHashes := append(left.data, right.data...)
hash := sha256.Sum256(preHashes)
mNode.data = hash[:]
}
mNode.Left = left
mNode.Right = right
return &mNode
}
func (b *Block) HashTransactions() []byte {
var transactions [][]byte
for _, tx := range b.Transactions {
transactions = append(transactions, tx.Serialize())
}
mTree := NewMerkleTree(transactions)
return mTree.RootNode.Data
}
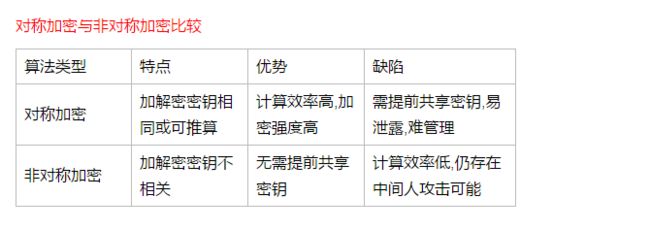
二、对称加密
对称加密(也叫私钥加密)指加密和解密使用相同(或可推导)密钥的加密算法。
特点
优点是加密效率高(速度快,空间占用小),加密强度高.缺点是需要提前分发密钥,易泄露,不安全,难管理。另外如何在不安全通道下分发密钥也是个问题。
适用于大量数据的加解密,不能用于签名场景
代表算法
DES(不够安全),3DES(不够安全),IDEA,AES
三、非对称加密
非对称加密(也叫公钥加密),顾名思义,加密密钥和解密密钥是不同的,分别称为公钥和私钥。 公钥一般是公开的,人人可获取的,私钥一般是个人自己持有,不能被他人获取。
一个小栗子, x * 13 * 77 % 1000 = x
特点
优点是公私钥分开,不安全通道也可使用;多方通信所需密钥少,维护简单。缺点是加解密速度慢,一般比对称加解密算法慢两到三个数量级;同时加密强度相比对称加密要差。
代表算法
RSA(不够安全),ECC(椭圆曲线系列算法)
四、数字签名
所谓数字签名就是签名人用自己的私钥对待签名数据的摘要进行加密得到的值就是签名值。签名者发送数据签名时需要把待签名数据和签名值一起发送给对方。
注意,签名对象并非待签名数据而是待签名数据的摘要,为什么呢?因为非对称加密的速度通常都比较慢,直接对原始数据私钥加密是很慢的而且也没有必要。
如何验证签名呢?接收方首先使用签名者的公钥对签名值解密即可得到摘要值,然后使用约定的算法对待签名数据进行散列运算后和解密得到的摘要值进行比较即可验证。
从以上数字签名的整个过程描述来看,数字签名的核心在于签名,在于证明这份数据是未被篡改的、签名者发出的、不可抵赖的。待签名数据本身的保密不是数字签名方案要考虑的问题。
比特币使用的是 ECDSA(Elliptic Curve Digital Signature Algorithm)算法(即椭圆曲线数字签名算法)来对交易进行签名
代表算法
DSA,ECDSA
便于理解可参考 数字签名场景
五、编码
这里引用《精通比特币》
为了更简洁方便地表示长串的数字,许多计算机系统会使用一种以数字和字母组成的大于十进制的表示法。例如,传统的十进制计数系统使用0-9十个数字,而十六进制系统使用了额外的 A-F 六个字母。一个同样的数字,它的十六进制表示就会比十进制表示更短。更进一步,Base64使用了26个小写字母、26个大写字母、10个数字以及两个符号(例如“+”和“/”),用于在电子邮件这样的基于文本的媒介中传输二进制数据。Base64通常用于编码邮件中的附件。Base58是一种基于文本的二进制编码格式,用在比特币和其它的加密货币中。这种编码格式不仅实现了数据压缩,保持了易读性,还具有错误诊断功能。Base58是Base64编码格式的子集,同样使用大小写字母和10个数字,但舍弃了一些容易错读和在特定字体中容易混淆的字符。具体地,Base58不含Base64中的0(数字0)、O(大写字母o)、l(小写字母L)、I(大写字母i),以及“+”和“/”两个字符。简而言之,Base58就是由不包括(0,O,l,I)的大小写字母和数字组成。
需要注意的是,Base58编码是不含校验信息的,Base58Check是一种常用在比特币中的Base58编码格式,增加了错误校验码来检查数据在转录中出现的错误。校验码长4个字节,添加到需要编码的数据之后。
为了使用Base58Check编码格式对数据(数字)进行编码,首先我们要对数据添加一个称作“版本字节”的前缀,这个前缀用来明确需要编码的数据的类型。例如,比特币地址的前缀是0(十六进制是0x00),而对私钥编码时前缀是128(十六进制是0x80)。
接下来,我们计算“双哈希”校验码,意味着要对之前的结果(前缀和数据)运行两次SHA256哈希算法:
checksum = SHA256(SHA256(prefix+data))
在产生的长32个字节的哈希值(两次哈希运算)中,我们只取前4个字节。这4个字节就作为校验码。校验码会添加到数据之后。结果由三部分组成:前缀、数据和校验码。